|
[Go to TOC]
Jamming-to-Signal (J/S) Ratio - Constant
Power [Saturated] Jamming
The following table contains a summary of the equations developed in this section.
![Jamming-to-Signal Ratio (J/S) - Constant Power [Saturated] Jamming - RF Cafe](images/imgt6D.gif)
This section derives the J/S ratio from the one-way range equation for J and
the two-way range equation for S, and deals exclusively with active (transmitting)
ECM devices or systems. Furthermore, the only purpose of the ECM considered is to
prevent, delay, or confuse the radar processing of target information.
By official definition, ECM can be either Jamming or Deception. This may be somewhat
confusing because almost any type of active ECM is commonly called "jamming", and
the calculations of ECM signal in the radar compared to the target signal in the
radar commonly refer to the "jamming-to-signal" ratio ("J-to-S" ratio). Therefore
this section uses the common jargon and the term "jammer" refers to any ECM transmitter,
and the term "jamming" refers to any ECM transmission, whether Deception or Concealment.
Jamming:
 "Official" jamming should more aptly be called Concealment
or Masking. Essentially, Concealment uses ECM to swamp the radar receiver
and hide the targets. Concealment (Jamming) usually uses some form of noise as the
transmitted ECM signal. In this section, Concealment will be called "noise" or "noise
jamming". "Official" jamming should more aptly be called Concealment
or Masking. Essentially, Concealment uses ECM to swamp the radar receiver
and hide the targets. Concealment (Jamming) usually uses some form of noise as the
transmitted ECM signal. In this section, Concealment will be called "noise" or "noise
jamming".
Deception: Deception might be better called Forgery. Deception uses ECM to forge
false target signals that the radar receiver accepts and processes as real targets.
"J" designates the ECM signal strength whether it originates from a noise jammer
or from a deception ECM system.
Basically, there are
two different methods of employing active ECM against hostile radars:
Self Protection ECM
Support ECM
For most practical purposes, Self Protection ECM is usually Deception and Support
ECM is usually noise jamming. As the name implies, Self Protection ECM is ECM that
is used to protect the platform that it is on. Self Protection ECM is often called
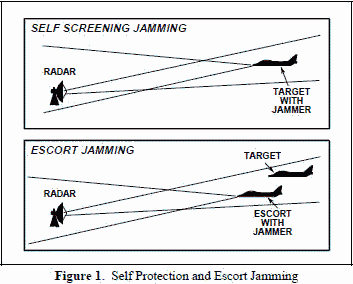
"self screening jamming", and also "DECM", which is an acronym for either "Defensive
ECM" or "Deception ECM". The top half of Figure 1 shows self screening jamming (DECM).
The bottom half of Figure 1 illustrates escort jamming which is a special case
of support jamming. If the escort platform is sufficiently close to the target,
the J-to-S calculations are the same as for DECM.
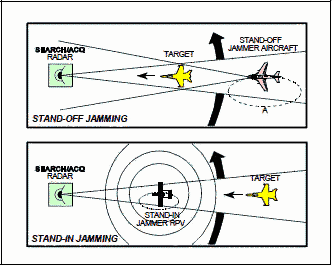
Support ECM is ECM radiated
from one platform and is used to protect other platforms. Figure 2 illustrates two
cases of support jamming - stand-off jamming (SOJ) and stand-in jamming (SIJ). For
SOJ the support jamming platform is maintaining an orbit at a long range from the
radar - usually beyond weapons range. For SIJ, a remotely piloted vehicle is orbiting
very close to the victim radar. Obviously, the jamming power required for the SOJ
to screen a target is much greater than the jamming power required for the SIJ to
screen the same target.
 When factoring ECM into the radar equation, the quantities of greatest interest
are "J-to-S" and Burn- Through Range. When factoring ECM into the radar equation, the quantities of greatest interest
are "J-to-S" and Burn- Through Range.
"J-to-S" is the ratio of the signal strength of the ECM signal (J) to the signal
strength of the target return signal (S). It is expressed as "J/S" and, in this
section, is always in dB. J usually (but not always) must exceed S by some amount
to be effective, therefore the desired result of a J/S calculation in dB is a positive
number. Burn-through Range is the radar to target range where the target return
signal can first be detected through the ECM and is usually slightly farther than
crossover range where J=S. It is usually the range where the J/S just equals the
minimum effective J/S (See Section 4-8).
The significance of "J-to-S" is sometimes misunderstood. The effectiveness of
ECM is not a direct mathematical function of "J-to-S". The magnitude of the "J-to-S"
required for effectiveness is a function of the particular ECM technique and of
the radar it is being used against. Different ECM techniques may very well require
different "J-to-S" ratios against the same radar. When there is sufficient "J-to-S"
for effectiveness, increasing it will rarely increase the effectiveness at a given
range. Because modern radars can have sophisticated signal processing and/or ECCM
capabilities, in certain radars too much "J-to-S" could cause the signal processor
to ignore the jamming, or activate special anti-jamming modes. Increasing "J-to-S"
(or the jammer power) does, however, allow the target aircraft to get much closer
to the threat radar before burn-through occurs, which essentially means more power
is better if it can be controlled when desired.
|
IMPORTANT NOTE: If the signal S is CW or PD and the Jamming J is amplitude modulated,
then the J used in the formula has to be reduced from the peak value (due to sin
x/x frequency distribution). The amount of reduction is dependent upon how much
of the bandwidth is covered by the jamming signal. To get an exact value, integrals
would have to be taken over the bandwidth. As a rule of thumb however:
- C If the frequency of modulation is less than the BW of the tracking radar reduce
J/S by 10 Log(duty cycle).
- C If the frequency of modulation is greater than the BW of the tracking radar
reduce J/S by 20 Log(duty cycle).
For example; if your jamming signal is square wave chopped (50% duty cycle) at
a 100 Hz rate while jamming a 1 kHz bandwidth receiver, then the J/S is reduced
by 3 dB from the maximum. If the duty cycle was 33%, then the reduction would be
4.8 dB. If the 50% and 33% duty cycle jamming signals were chopped at a 10 kHz (vice
the 100 Hz) rate, the rule of thumb for jamming seen by the receiver would be down
6 dB and 9.6 dB, respectively, from the maximum since the 10 kHz chopping rate is
greater than the 1 kHz receiver BW.
|
Figure 3 is radar jamming visualized. The Physical concept of Figure 3 shows
a monostatic radar that is the same as Figure 1, Section 4-4, and a jammer (transmitter)
to radar (receiver) that is the same as Figure 3, Section 4-3. In other words, Figure
3 is simply the combination of the previous two visual concepts where there is only
one receiver (the radar's).
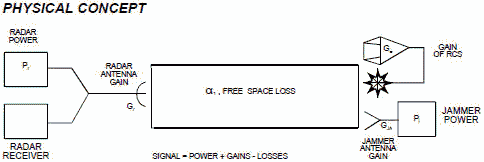
Figure 3 - Radar Jamming Visualized
J/S for DECM vs. Monostatic Radar
The equivalent circuit shown in Figure 4 applies to jamming monostatic radars
with either DECM or support ECM. For DECM (or escort) v.s. a monostatic radar, the
jammer is on the target and the radar receive and transmit antennas are collocated
so the three ranges and three space loss factors (α's)
are the same.

Figure 4 - Monostatic Radar ECM Equivalent Circuit
J-S Ratio (Monostatic) The ratio of the power received
(Pr1 or J) from the jamming signal transmitted from the target to the
power received (Pr2 or S) from the radar skin return from the target
equals J/S.
From the one way range equation in Section 4-3:
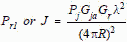 [1] [1]
Note: To avoid having to include additional terms for these calculations, always
combine any transmission line loss with antenna gain.
From the two way range equation in Section 4.4:
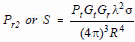 [2] [2]
so  [3] [3]
* Keep R and F in the same units.
On reducing the above equation to log form we have:
10log J/S = 10log Pj + 10log Gja - 10log Pt
- 10log Gt - 10log σ + 10log 4π + 20log R
[4]
or 10log J/S = 10log Pj + 10log Gja - 10log Pt
- 10log Gt - 10log σ + 10.99 dB + 20log R [5]
Note: Neither f nor λ terms are part of the final form of equation [3] and equation
[5].
J/S Calculations (Monostatic) Using a One Way Free Space
Loss - The simplified radar equations developed in previous sections can
be used to express J/S.
From the one way range equation Section 4-3:
10log (Pr1 or J) = 10log Pj + 10log Gja + 10log
Gr - α1 (in dB)
[6]
From the two way range equation in Section 4.4:
10log (Pr2 or S) = 10log Pt + 10log Gt + 10log
Gr + Gσ - 2α1 (in dB)
[7]
10log (J/S) = 10log Pj + 10log Gja - 10log Pt
- 10log Gt - Gσ + α1
(in dB) [8]
Note: To avoid having to include additional terms for these calculations, always
combine any transmission line loss with antenna gain. The 20log f1 term
in -Gσ cancels the 20log f1 term in α1.

J/S for DECM vs. Bistatic Radar
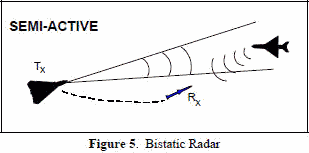 The semi-active missile
illustrated in Figure 5 is the typical bistatic radar which would require the target
to have self protection ECM to survive. In this case, the jammer is on the target
and the target to missile receiver range is the same as the jammer to receiver range,
but the radar to target range is different. Therefore, only two of the ranges and
two of the "'s (Figure 6.) are the same. The semi-active missile
illustrated in Figure 5 is the typical bistatic radar which would require the target
to have self protection ECM to survive. In this case, the jammer is on the target
and the target to missile receiver range is the same as the jammer to receiver range,
but the radar to target range is different. Therefore, only two of the ranges and
two of the "'s (Figure 6.) are the same.
In the following equations:
"Tx = The one-way space loss from the radar
transmitter to the target
for range RTx
"Rx = The one-way space loss from the target to the missile receiver for range
RRx
Like the monostatic radar, the bistatic jamming and reflected target signals
travel the same path from the target and enter the receiver (missile in this case)
via the same antenna. In both monostatic and bistatic J/S equations this common
range cancels, so both J/S equations are left with an RTx or 20 log RTx
term. Since in the monostatic case RTx = RRx and
αTx = αRx
, only R or α1 is used in the equations.
Therefore, the bistatic J/S equations [11], [13], or [14] will work for monostatic
J/S calculations, but the opposite is only true if bistatic RTx and
αTx terms are used for R or
α1 terms in monostatic equations [3], [5],
and [8].
The equivalent circuit shown in Figure 6 applies to jamming bistatic radar. For
DECM (or escort) vs. a bistatic radar, the jammer is on the target and the radar
receive and transmit antennas are at separate locations so only two of the three
ranges and two of the three space loss factors ("'s) are the same.
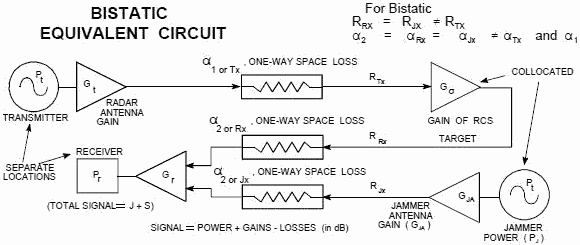
Figure 6 - Bistatic Radar ECM Equivalent Circuit
J-to-S Ratio (Bistatic) When the radar's transmit
antenna is located remotely from the receiving antenna (Figure 6), the ratio of
the power received (Pr1 or J) from the jamming signal transmitted from
the target to the power received (Pr2 or S) from the radar skin return
from the target equals J/S. For jammer effectiveness J normally has to be greater
than S.
From the one way range equation in Section 4-3: 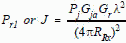 (RJx = RRx)
[9] (RJx = RRx)
[9]
From the two way range equation in Section 4.4: 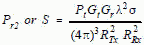 [10] [10]
so  [11] [11]
* Keep R and F in the same units.
On reducing the above equation to log form we have:
10log J/S = 10log Pj + 10log Gja - 10log Pt
- 10log Gt - 10log σ + 10log 4π + 20log RTx
[12]
or 10log J/S = 10log Pj + 10log Gja - 10log Pt
- 10log Gt - 10log σ + 10.99 dB + 20log RTx
[13]
Note: To avoid having to include additional terms for these calculations, always
combine any transmission line loss with antenna gain. Neither f nor λ terms are
part of the final form of equation [11] and equation [13].
Bistatic J/S Calculations (Bistatic) Using a One Way Free
Space Loss - The simplified radar equations developed in previous sections
can be used to express J/S.
From the one way range equation in Section 4-3:
10log (Pr1 or J) = 10log Pj + 10log Gja + 10log
Gr - αRx (all factors dB)
[14]
From the two way range equation in Section 4-4:
10log (Pr2 or S) = 10log Pt + 10log Gt + 10log
Gr + Gσ - αTx -
αRx (all factors dB) [15]
10log (J/S) = 10log Pj + 10log Gja - 10log Pt
- 10log Gt - Gσ + αTx (all factors
dB) [16]
Note: To avoid having to include additional terms for these calculations, always
combine any transmission line loss with antenna gain. The 20log f1 term
in -Gσ cancels the 20log f1 term in α1.

Saturated J/S (Monostatic) Example (Constant Power Jamming)
Assume that a 5 GHz radar has a 70 dBm signal fed through a 5 dB loss transmission
line to an antenna that has 45 dB gain. An aircraft is flying 31 km from the radar.
The aft EW antenna has -1 dB gain and a 5 dB line loss to the EW receiver (there
is an additional loss due to any antenna polarization mismatch but that loss will
not be addressed in this problem). The aircraft has a jammer that provides 30 dBm
saturated output if the received signal is above -35 dBm. The jammer feeds a 10
dB loss transmission line which is connected to an antenna with a 5 dB gain. If
the RCS of the aircraft is 9 m2, what is the J/S level received by the
tracking radar?
Answer: The received signal at the jammer is the same as the example in Section
4-3, i.e. answer (1) = -32.3 dBm @ 5 GHz. Since the received signal is above -35
dBm, the jammer will operate in the saturated mode, and equation [5] can be used.
(See Section 4-10 for an example of a jammer operating in the linear region.)
10log J/S = 10log Pj + 10log Gja - 10log Pt
- 10log Gt - 10log σ + 10.99 dB + 20log R
Note: the respective transmission line losses will be combined with antenna gains,
i.e. -5 + 45 = 40 dB & -10 +5 = -5 dB.
10log J/S = 30 - 5 - 70 - 40 - 9.54 + 10.99 + 89.8 = 6.25 dB @ 5 GHz*
* The answer is still 6.25 dB if the tracking radar operates at 7 GHz provided
the antenna gains and the aircraft RCS are the same at both frequencies.
In this example, there is inadequate jamming power at each frequency if the J/S
needs to be 10 dB or greater to be effective. One solution would be to replace the
jammer with one that has a greater power output. If the antenna of the aircraft
and the radar are not the proper polarization, additional power will also be required
(see Section 3-2).
Table of Contents for Electronics Warfare and Radar Engineering Handbook
Introduction |
Abbreviations | Decibel | Duty
Cycle | Doppler Shift | Radar Horizon / Line
of Sight | Propagation Time / Resolution | Modulation
| Transforms / Wavelets | Antenna Introduction
/ Basics | Polarization | Radiation Patterns |
Frequency / Phase Effects of Antennas |
Antenna Near Field | Radiation Hazards |
Power Density | One-Way Radar Equation / RF Propagation
| Two-Way Radar Equation (Monostatic) |
Alternate Two-Way Radar Equation |
Two-Way Radar Equation (Bistatic) |
Jamming to Signal (J/S) Ratio - Constant Power [Saturated] Jamming
| Support Jamming | Radar Cross Section (RCS) |
Emission Control (EMCON) | RF Atmospheric
Absorption / Ducting | Receiver Sensitivity / Noise |
Receiver Types and Characteristics |
General Radar Display Types |
IFF - Identification - Friend or Foe | Receiver
Tests | Signal Sorting Methods and Direction Finding |
Voltage Standing Wave Ratio (VSWR) / Reflection Coefficient / Return
Loss / Mismatch Loss | Microwave Coaxial Connectors |
Power Dividers/Combiner and Directional Couplers |
Attenuators / Filters / DC Blocks |
Terminations / Dummy Loads | Circulators
and Diplexers | Mixers and Frequency Discriminators |
Detectors | Microwave Measurements |
Microwave Waveguides and Coaxial Cable |
Electro-Optics | Laser Safety |
Mach Number and Airspeed vs. Altitude Mach Number |
EMP/ Aircraft Dimensions | Data Busses | RS-232 Interface
| RS-422 Balanced Voltage Interface | RS-485 Interface |
IEEE-488 Interface Bus (HP-IB/GP-IB) | MIL-STD-1553 &
1773 Data Bus | This HTML version may be printed but not reproduced on websites.
|



























![Jamming-to-Signal Ratio (J/S) - Constant Power [Saturated] Jamming - RF Cafe](images/imgt6D.gif)
 "Official" jamming should more aptly be called Concealment
or Masking. Essentially, Concealment uses ECM to swamp the radar receiver
and hide the targets. Concealment (Jamming) usually uses some form of noise as the
transmitted ECM signal. In this section, Concealment will be called "noise" or "noise
jamming".
"Official" jamming should more aptly be called Concealment
or Masking. Essentially, Concealment uses ECM to swamp the radar receiver
and hide the targets. Concealment (Jamming) usually uses some form of noise as the
transmitted ECM signal. In this section, Concealment will be called "noise" or "noise
jamming". When factoring ECM into the radar equation, the quantities of greatest interest
are "J-to-S" and Burn- Through Range.
When factoring ECM into the radar equation, the quantities of greatest interest
are "J-to-S" and Burn- Through Range.

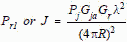 [1]
[1]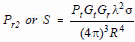 [2]
[2] [3]
[3]
 The semi-active missile
illustrated in Figure 5 is the typical bistatic radar which would require the target
to have self protection ECM to survive. In this case, the jammer is on the target
and the target to missile receiver range is the same as the jammer to receiver range,
but the radar to target range is different. Therefore, only two of the ranges and
two of the "'s (Figure 6.) are the same.
The semi-active missile
illustrated in Figure 5 is the typical bistatic radar which would require the target
to have self protection ECM to survive. In this case, the jammer is on the target
and the target to missile receiver range is the same as the jammer to receiver range,
but the radar to target range is different. Therefore, only two of the ranges and
two of the "'s (Figure 6.) are the same.
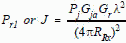 (RJx = RRx)
[9]
(RJx = RRx)
[9]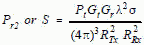 [10]
[10] [11]
[11]
