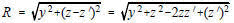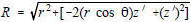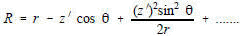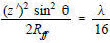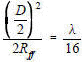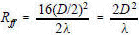Electronic Warfare and Radar Systems Engineering Handbook
|
|
ANTENNA NEAR FIELD As noted in the sections on RF propagation and the radar equation, electromagnetic radiation expands spherically (Figure 1) and the power density at a long range (R) from the transmitting antenna is: [1]
When the range is large, the spherical surface of uniform power density appears flat to a receiving antenna which is very small compared to the surface of the sphere. This is why the far field wave front is considered planar and the rays approximately parallel. Also, it is apparent that at some shorter range, the spherical surface no longer appears flat, even to a very small receiving antenna. The distances where the planer, parallel ray approximation breaks down is known as the near field. The crossover distance between near and far fields (Rff) is taken to be where the phase error is 1/16 of a wavelength, or about 22.5°.
[2]
While the above analogy provides an image of the difference between the near and far fields, the relationship must be defined as a characteristic of the transmitting antenna.
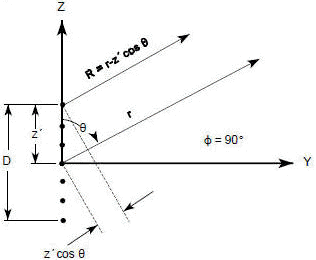
Actual antennas, of course, are not ideal point source radiators but have physical dimensions. If the transmitting antenna placed at the origin of Figure 1 occupies distance D along the Z-axis and is boresighted along the Y-axis (ф = 90), then the geometry of point P on the sphere is represented in two dimensions by Figure 2. For convenience, the antenna is represented by a series of point sources in an array. When point P is close to the antenna, as in Figure 2, then the difference in distance of the two rays r and R taken respectively from the center of the antenna and the outer edge of the antenna varies as point P changes.
From Figure 2, the following applies: [3] r2 = z2 + y2 [4] z = r cos θ [5] y = r sin θ and [6]
Substituting [3] and [4] into [6]
[7] which puts point P into spherical coordinates. Equation [7] can be expanded by the binomial theorem which for the first three terms, reduces to:
[8] In the parallel ray approximation for far field calculations (Figure 3) the third term of [8] is neglected. The distance where the far field begins (Rff) (or where the near field ends) is the value of r when the error in R due to neglecting the third term of equation [8], equals 1/16 of a wavelength. Rff is usually calculated on boresight, so θ = 90° and the second term of equation [8] equals zero (Cos 90° = 0), therefore from Figure 3, where D is the antenna dimension, Rff is found by equating the third term of [8] to 1/16 wavelength.
Sin θ = Sin 90 = 1 and z' = D/2 so:
[9]
Equation [9] is the standard calculation of far field given in all references. Besides [9] some general rules of thumb for far field conditions are:
r >> D or r >> λ If the sphere and point P are a very great distance from the antenna, then the rays are very nearly parallel and this difference is small as in Figure 3.
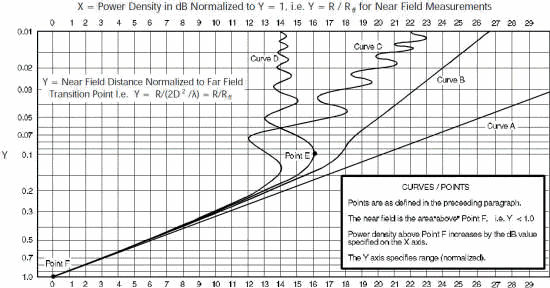
Figure 3 - Far Field Parallel Ray Approximation for Calculations. The power density within the near field varies as a function of the type of aperture illumination and is less than would be calculated by equation [1]. Thus, in the antenna near field there is stored energy. (The complex radiation field equations have imaginary terms indicating reactive power.) Figure 4 shows normalized power density for three different illuminations.
Curve A is for reference only and shows how power density would vary if it were calculated using equation [1]. Curve B shows power density variations on axis for an antenna aperture with a cosine amplitude distribution. This is typical of a horn antenna in the H-plane. Curve C shows power density variations on axis for a uniformly illuminated antenna aperture or for a line source. This is typical of a horn antenna in the E-plane. Curve D shows power density variations on axis for an antenna aperture with a tapered illumination. Generally the edge illumination is approximately -10 dB from the center illumination and is typical of a parabolic dish antenna. Point E - For radiation safety purposes, a general rule of thumb for tapered illumination is that the maximum safe level of 10 mW/cm2 (-200 V/m) is reached in the near field if the level at R reaches 0.242 mW/cm2 as can be ff verified by computing the power density at point E in Figure 4. (10 mW/cm2 at point E extrapolates to 0.242 mW/cm2 [16 dB lower] at R=Rff , or Y axis value =1). Figure 1 in Section 3-6 depicts more precise values for radiation hazard exposure. Point F - Far Field Point. At distances closer to the source than this point (near field), the power density from any given antenna is less than that predicted using Curve A. At farther distances, (far field) power densities from all types of antennas are the same.
Figure 4 - Antenna Near-Field On-Axis Power Density (Normalized) For Various Aperture Illuminations For Various Aperture Illuminations FOR FAR FIELD MEASUREMENTS:
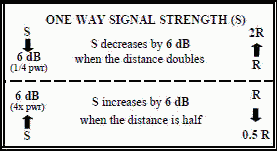
When free space measurements are performed at a known distance from a source, it is often necessary to know if the measurements are being performed in the far field. As can be seen from Curve A on Figure 4, if the distance is halved (going from 1.0 to 0.5 on the Y axis), the power density will increase by 6 dB (going from 0 to 6 dB on the X axis). Each reduction in range by ½ results in further 6 dB increases. As previously mentioned, Curve A is drawn for reference only in the near field region, since at distances less than Rff the power density increases less than 6 dB when the range is halved. In the far field, all curves converge and Equation [1] applies. When a measurement is made in free space, a good check to ensure that is was performed in the far field is to repeat the measurement at twice the distance. The power should decrease by exactly 6 dB. A common error is to use 3 dB (the half power point) for comparison. Conversely, the power measurement can be repeated at half the distance, in which case you would look for a 6 dB increase, however the conclusion is not as sure, because the first measurement could have been made in the far field, and the second could have been made in the near field.
Table of Contents for Electronics Warfare and Radar Engineering Handbook Introduction | Abbreviations | Decibel | Duty Cycle | Doppler Shift | Radar Horizon / Line of Sight | Propagation Time / Resolution | Modulation | Transforms / Wavelets | Antenna Introduction / Basics | Polarization | Radiation Patterns | Frequency / Phase Effects of Antennas | Antenna Near Field | Radiation Hazards | Power Density | One-Way Radar Equation / RF Propagation | Two-Way Radar Equation (Monostatic) | Alternate Two-Way Radar Equation | Two-Way Radar Equation (Bistatic) | Jamming to Signal (J/S) Ratio - Constant Power [Saturated] Jamming | Support Jamming | Radar Cross Section (RCS) | Emission Control (EMCON) | RF Atmospheric Absorption / Ducting | Receiver Sensitivity / Noise | Receiver Types and Characteristics | General Radar Display Types | IFF - Identification - Friend or Foe | Receiver Tests | Signal Sorting Methods and Direction Finding | Voltage Standing Wave Ratio (VSWR) / Reflection Coefficient / Return Loss / Mismatch Loss | Microwave Coaxial Connectors | Power Dividers/Combiner and Directional Couplers | Attenuators / Filters / DC Blocks | Terminations / Dummy Loads | Circulators and Diplexers | Mixers and Frequency Discriminators | Detectors | Microwave Measurements | Microwave Waveguides and Coaxial Cable | Electro-Optics | Laser Safety | Mach Number and Airspeed vs. Altitude Mach Number | EMP/ Aircraft Dimensions | Data Busses | RS-232 Interface | RS-422 Balanced Voltage Interface | RS-485 Interface | IEEE-488 Interface Bus (HP-IB/GP-IB) | MIL-STD-1553 & 1773 Data Bus | This HTML version may be printed but not reproduced on websites. Related Pages on RF Cafe - Antennas - Hardware & Controls - Antennas - Manufacturers & Services - Test Equipment & Calibration - Antenna Measurement - Antenna Introduction / Basics - Near-Field / Far-Field Transition Distance - Intro to Wave Propagation, Transmission Lines, Antennas - Antenna, Electromagnetics & X-mission Line Simulators |
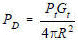
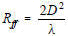 where λ is the wavelength and D is the largest dimension of
the transmit antenna.
where λ is the wavelength and D is the largest dimension of
the transmit antenna. 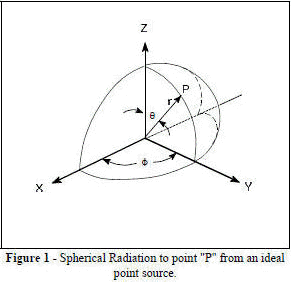 If the same size antenna is used for multiple
frequencies, Rff will increase with increasing frequency. However, if various size antennas are used for different
frequencies and each antenna is designed with D as a function of λ (λ/2 to 100λ), then Rff will vary from c/2f
to 20000c/f. In this case Rff will decrease with increasing frequency. For example: a 10λ antenna at 3 GHZ has a D of 100
cm and corresponding Rff of 20 m, while a 10λ antenna at 30 GHz has a D of 10 cm and corresponding Rff
of 2 m.
If the same size antenna is used for multiple
frequencies, Rff will increase with increasing frequency. However, if various size antennas are used for different
frequencies and each antenna is designed with D as a function of λ (λ/2 to 100λ), then Rff will vary from c/2f
to 20000c/f. In this case Rff will decrease with increasing frequency. For example: a 10λ antenna at 3 GHZ has a D of 100
cm and corresponding Rff of 20 m, while a 10λ antenna at 30 GHz has a D of 10 cm and corresponding Rff
of 2 m.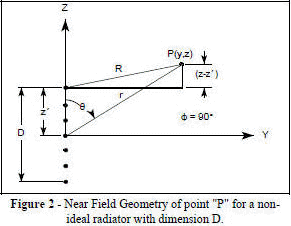 Derivation of equation [2] is given as follows:
Derivation of equation [2] is given as follows: