Electronic Warfare and Radar Systems Engineering Handbook |
|
TRANSFORMS / WAVELETS Transform Analysis Signal processing using a transform analysis for calculations is a technique used to simplify or accelerate problem solution. For example, instead of dividing two large numbers, we might convert them to logarithms, subtract them, then look-up the anti-log to obtain the result. While this may seem a three-step process as opposed to a one-step division, consider that long-hand division of a four digit number by a three digit number, carried out to four places requires three divisions, 3-4 multiplication*s, and three subtractions. Computers process additions or subtractions much faster than multiplications or divisions, so transforms are sought which provide the desired signal processing using these steps.
Other types of transforms include the Fourier transform, which is used to decompose or separate a waveform into a sum of sinusoids of different frequencies. It transforms our view of a signal from time based to frequency based. Figure 1 depicts how a square wave is formed by summing certain particular sine waves. The waveform must be continuous, periodic, and almost everywhere differentiable. The Fourier transform of a sequence of rectangular pulses is a series of sinusoids. The envelope of the amplitude of the coefficients of this series is a waveform with a Sin X/X shape. For the special case of a single pulse, the Fourier series has an infinite series of sinusoids that are present for the duration of the pulse.
In order to process a signal digitally, we need to sample the signal frequently enough to create a complete “picture” of the signal. The discrete Fourier transform (DFT) may be used in this regard. Samples are taken at uniform time intervals as shown in Figure 2 and processed.
Figure 4 depicts the process pictorially: The vectors in the figure just happen to be pointing in a cardinal direction because the strobe frequencies are all multiples of the vector (phasor) rotation rate, but that is not normally the case. Usually the vectors will point in a number of different directions, with a resultant in some direction other than straight up.
In addition, sampling normally has to taken at or above twice the rate of interest (also known as the Nyquist rate), otherwise ambiguous results may be obtained.
Figure 4. Phasor Representation
Fast Fourier Transforms
For example, in an eight filter bank, a DFT would require 512 computations, while an FFT would only require 56, significantly speeding up processing time.
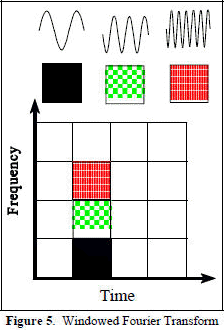
Windowed Fourier Transform The Fourier transform is continuous, so a windowed Fourier transform (WFT) is used to analyze non-periodic signals as shown in Figure 5. With the WFT, the signal is divided into sections (one such section is shown in Figure 5) and each section is analyzed for frequency content. If the signal has sharp transitions, the input data is windowed so that the sections converge to zero at the endpoints. Because a single window is used for all frequencies in the WFT, the resolution of the analysis is the same (equally spaced) at all locations in the time-frequency domain.
The FFT works well for signals with smooth or uniform frequencies, but it has been found that other transforms work better with signals having pulse type characteristics, time-varying (non-stationary) frequencies, or odd shapes. The FFT also does not distinguish sequence or timing information. For example, if a signal has two frequencies (a high followed by a low or vice versa), the Fourier transform only reveals the frequencies and relative amplitude, not the order in which they occurred. So Fourier analysis works well with stationary, continuous, periodic, differentiable signals, but other methods are needed to deal with non-periodic or non-stationary signals. Wavelet Transform The Wavelet transform has been evolving for some time. Mathematicians theorized its use in the early 1900's. While the Fourier transform deals with transforming the time domain components to frequency domain and frequency analysis, the wavelet transform deals with scale analysis, that is, by creating mathematical structures that provide varying time/frequency/amplitude slices for analysis. This transform is a portion (one or a few cycles) of a complete waveform, hence the term wavelet.
In wavelet analysis, the scale that one uses in looking at data plays a special role. Wavelet algorithms process data at different scales or resolutions. If we look at a signal with a large "window," we would notice gross features. Similarly, if we look at a signal with a small "window," we would notice small discontinuities as shown in Figure 6. The result in wavelet analysis is to "see the forest and the trees." A way to achieve this is to have short high-frequency fine scale functions and long low-frequency ones. This approach is known as multi-resolution analysis. For many decades, scientists have wanted more appropriate functions than the sines and cosines (base functions) which comprise Fourier analysis, to approximate choppy signals. (Although Walsh transforms work if the waveform is periodic and stationary). By their definition, sine and cosine functions are non-local (and stretch out to infinity), and therefore do a very poor job in approximating sharp spikes. But with wavelet analysis, we can use approximating functions that are contained neatly in finite (time/frequency) domains. Wavelets are well-suited for approximating data with sharp discontinuities. The wavelet analysis procedure is to adopt a wavelet prototype function, called an "analyzing wavelet" or "mother wavelet." Temporal analysis is performed with a contracted, high-frequency version of the prototype wavelet, while frequency analysis is performed with a dilated, low-frequency version of the prototype wavelet. Because the original signal or function can be represented in terms of a wavelet expansion (using coefficients in a linear combination of the wavelet functions), data operations can be performed using just the corresponding wavelet coefficients as shown in Figure 7.
Fourier transforms deal with just two basis functions (sine and cosine), while there are an infinite number of wavelet basis functions. The freedom of the analyzing wavelet is a major difference between the two types of analyses and is important in determining the results of the analysis. The “wrong” wavelet may be no better (or even far worse than) than the Fourier analysis. A successful application presupposes some expertise on the part of the user. Some prior knowledge about the signal must generally be known in order to select the most suitable distribution and adapt the parameters to the signal. Some of the more common ones are shown in Figure 8. There are several wavelets in each family, and they may look different than those shown. Somewhat longer in duration than these functions, but significantly shorter than infinite sinusoids is the cosine packet shown in Figure 9. Wavelet Comparison With Fourier Analysis While a typical Fourier transform provides frequency content information for samples within a given time interval, a perfect wavelet transform records the start of one frequency (or event), then the start of a second event, with amplitude added to or subtracted from, the base event.
Wavelets are especially useful in analyzing transients or time-varying signals. The input signal shown in Figure 9 consists of a sinusoid whose frequency changes in stepped increments over time. The power of the spectrum is also shown. Classical Fourier analysis will resolve the frequencies but cannot provide any information about the times at which each occurs. Wavelets provide an efficient means of analyzing the input signal so that frequencies and the times at which they occur can be resolved. Wavelets have finite duration and must also satisfy additional properties beyond those normally associated with standard windows used with Fourier analysis. The result after the wavelet transform is applied is the plot shown in the lower right. The wavelet analysis correctly resolves each of the frequencies and the time when it occurs. A series of wavelets is used in example 2.
Wavelet Applications Some fields that are making use of wavelets are: astronomy, acoustics, nuclear engineering, signal and image processing (including fingerprinting), neurophysiology, music, magnetic resonance imaging, speech discrimination, optics, fractals, turbulence, earthquake-prediction, radar, human vision, and pure mathematics applications. See October 1996 IEEE Spectrum article entitled “Wavelet Analysis”, by Bruce, Donoho, and Gao.
Table of Contents for Electronics Warfare and Radar Engineering Handbook Introduction | Abbreviations | Decibel | Duty Cycle | Doppler Shift | Radar Horizon / Line of Sight | Propagation Time / Resolution | Modulation | Transforms / Wavelets | Antenna Introduction / Basics | Polarization | Radiation Patterns | Frequency / Phase Effects of Antennas | Antenna Near Field | Radiation Hazards | Power Density | One-Way Radar Equation / RF Propagation | Two-Way Radar Equation (Monostatic) | Alternate Two-Way Radar Equation | Two-Way Radar Equation (Bistatic) | Jamming to Signal (J/S) Ratio - Constant Power [Saturated] Jamming | Support Jamming | Radar Cross Section (RCS) | Emission Control (EMCON) | RF Atmospheric Absorption / Ducting | Receiver Sensitivity / Noise | Receiver Types and Characteristics | General Radar Display Types | IFF - Identification - Friend or Foe | Receiver Tests | Signal Sorting Methods and Direction Finding | Voltage Standing Wave Ratio (VSWR) / Reflection Coefficient / Return Loss / Mismatch Loss | Microwave Coaxial Connectors | Power Dividers/Combiner and Directional Couplers | Attenuators / Filters / DC Blocks | Terminations / Dummy Loads | Circulators and Diplexers | Mixers and Frequency Discriminators | Detectors | Microwave Measurements | Microwave Waveguides and Coaxial Cable | Electro-Optics | Laser Safety | Mach Number and Airspeed vs. Altitude Mach Number | EMP/ Aircraft Dimensions | Data Busses | RS-232 Interface | RS-422 Balanced Voltage Interface | RS-485 Interface | IEEE-488 Interface Bus (HP-IB/GP-IB) | MIL-STD-1553 & 1773 Data Bus | This HTML version may be printed but not reproduced on websites. |
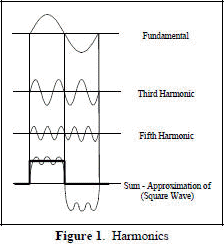 Fourier Transform
Fourier Transform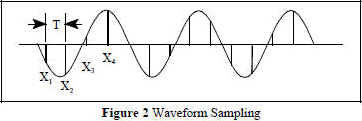 Digital
Sampling of Waveforms
Digital
Sampling of Waveforms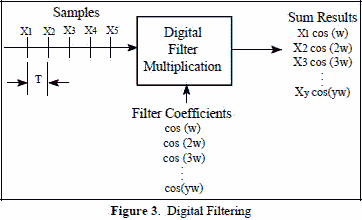 If the digital information
is multiplied by the Fourier coefficients, a digital filter is created as shown Figure 3. If the sum of the resultant components is zero, the
filter has ignored (notched out) that frequency sample. If the sum is a relatively large number, the filter has passed the signal. With the
single sinusoid shown, there should be only one resultant. (Note that being “zero” and relatively large may just mean below or above the filter*s
cutoff threshold)
If the digital information
is multiplied by the Fourier coefficients, a digital filter is created as shown Figure 3. If the sum of the resultant components is zero, the
filter has ignored (notched out) that frequency sample. If the sum is a relatively large number, the filter has passed the signal. With the
single sinusoid shown, there should be only one resultant. (Note that being “zero” and relatively large may just mean below or above the filter*s
cutoff threshold)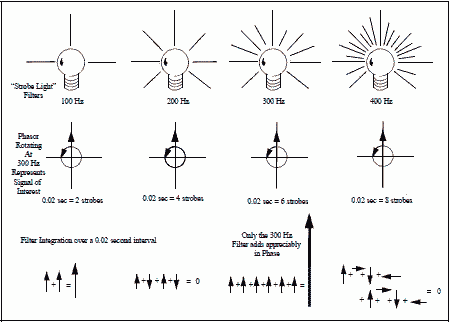
 One problem with this type of processing is the large number
of additions, subtractions, and multiplications which are required to reconstruct the output waveform. The Fast Fourier transform (FFT) was
developed to reduce this problem. It recognizes that because the filter coefficients are sine and cosine waves, they are symmetrical about 90,
180, 270, and 360 degrees. They also have a number of coefficients equal either to one or zero, and duplicate coefficients from filter to filter
in a multibank arrangement. By waiting for all of the inputs for the bank to be received, adding together those inputs for which coefficients
are the same before performing multiplications, and separately summing those combinations of inputs and products which are common to more than
one filter, the required amount of computing may be cut drastically.
One problem with this type of processing is the large number
of additions, subtractions, and multiplications which are required to reconstruct the output waveform. The Fast Fourier transform (FFT) was
developed to reduce this problem. It recognizes that because the filter coefficients are sine and cosine waves, they are symmetrical about 90,
180, 270, and 360 degrees. They also have a number of coefficients equal either to one or zero, and duplicate coefficients from filter to filter
in a multibank arrangement. By waiting for all of the inputs for the bank to be received, adding together those inputs for which coefficients
are the same before performing multiplications, and separately summing those combinations of inputs and products which are common to more than
one filter, the required amount of computing may be cut drastically.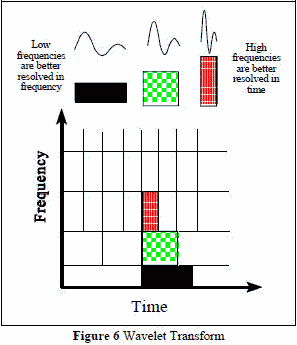 The wavelet transform has the ability to identify frequency
(or scale) components, simultaneously with their location(s) in time. Additionally, computations are directly proportional to the length of
the input signal. They require only N multiplications (times a small constant) to convert the waveform. For the previous eight filter bank example,
this would be about twenty calculations, vice 56 for the FFT.
The wavelet transform has the ability to identify frequency
(or scale) components, simultaneously with their location(s) in time. Additionally, computations are directly proportional to the length of
the input signal. They require only N multiplications (times a small constant) to convert the waveform. For the previous eight filter bank example,
this would be about twenty calculations, vice 56 for the FFT.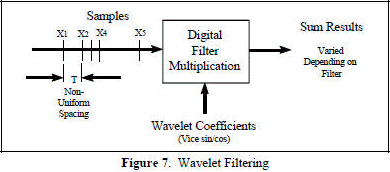 If one further
chooses the best wavelets adapted to the data, or truncates the coefficients below some given threshold, the data is sparsely represented. This
"sparse coding" makes wavelets an excellent tool in the field of data compression. For instance, the FBI uses wavelet coding to store fingerprints.
Hence, the concept of wavelets is to look at a signal at various scales and analyze it with various resolutions.
If one further
chooses the best wavelets adapted to the data, or truncates the coefficients below some given threshold, the data is sparsely represented. This
"sparse coding" makes wavelets an excellent tool in the field of data compression. For instance, the FBI uses wavelet coding to store fingerprints.
Hence, the concept of wavelets is to look at a signal at various scales and analyze it with various resolutions.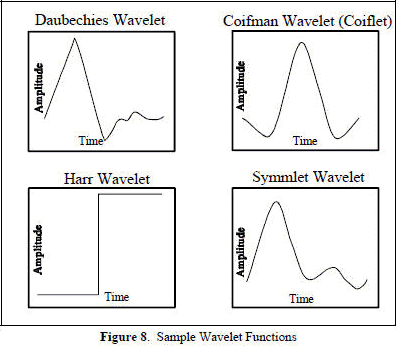 Analyzing Wavelet Functions
Analyzing Wavelet Functions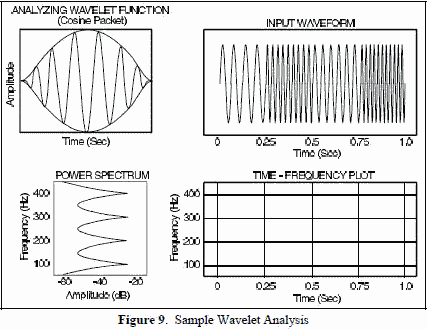 Example 1.
Example 1. Example 2.
Example 2.