Electronic Warfare and Radar Systems Engineering Handbook |
|
ANTENNA INTRODUCTION / BASICS Rules of Thumb: 1. The Gain of an antenna with losses is given by:
2. Gain of rectangular X-Band Aperture G = 1.4 LW Where: Length (L) and Width (W) are in cm
G = d2η Where: d = antenna diameter in cm η = aperture efficiency 4. Gain of an isotropic antenna radiating in a uniform spherical pattern is one (0 dB).
5. Antenna with a 20 degree beamwidth has a 20 dB gain.
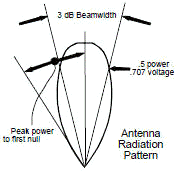
6. 3 dB beamwidth is approximately equal to the angle from the peak of the power to the first null (see figure at right).
7. Parabolic Antenna Beamwidth: Where: BW = antenna beamwidth; λ = wavelength; d = antenna diameter.
The gain or directivity of an antenna is the ratio of the radiation intensity in a given direction to the radiation intensity averaged over all directions. Quite often directivity and gain are used interchangeably. The difference is that directivity neglects antenna losses such as dielectric, resistance, polarization, and VSWR losses. Since these losses in most classes of antennas are usually quite small, the directivity and gain will be approximately equal (disregarding unwanted pattern characteristics). Normalizing a radiation pattern by the integrated total power yields the directivity of the antenna. This concept in shown in equation form by: [1]
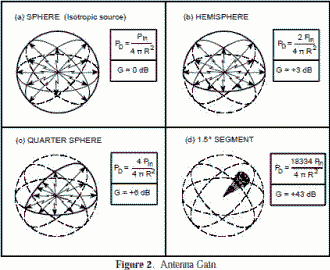
Where D(θ,ф) is the directivity in dB, and the radiation pattern power in a specific direction is Pd(θ,ф), which is normalized by the total integrated radiated power. Another important concept is that when the angle in which the radiation is constrained is reduced, the directive gain goes up. For example, using an isotropic radiating source, the gain would be 0 dB by definition (Figure 2(a)) and the power density (Pd) at any given point would be the power in (Pin) divided by the surface area of the imaginary sphere at a distance R from the source. If the spacial angle was decreased to one hemisphere (Figure 2(b)), the power radiated, Pin, would be the same but the area would be half as much, so the gain would double to 3 dB. Likewise if the angle is a quarter sphere, (Figure 2(c)), the gain would be 6 dB. Figure 2(d) shows a pencil beam. The gain is independent of actual power output and radius (distance) at which measurements are taken.
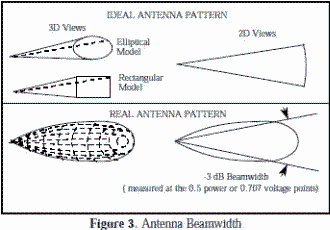
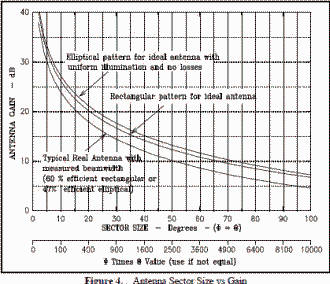
Real antennas are different, however, and do not have an ideal radiation distribution. Energy varies with angular displacement and losses occur due to sidelobes. However, if we can measure the pattern, and determine the beamwidth we can use two (or more) ideal antenna models to approximate a real antenna pattern as shown in Figure 3. Assuming the antenna pattern is uniform, the gain is equal to the area of the isotropic sphere (4πr2) divided by the sector (cross section) area.
It can be shown that: [3]
From this point, two different models are presented: (1) Approximating an antenna pattern using an elliptical area, and (2) Approximating an antenna pattern using a rectangular area.
Approximating the antenna pattern as an elliptical area: [4] The second term in the equation above is very close to equation [3]. For a very directional radar dish with a beamwidth of 1° and an average efficiency of 55%: Ideally: G = 52525, or in dB form: 10 log G =10 log 52525 = 47.2 dB With efficiency taken into account, G = 0.55(52525) = 28888, or in log form: 10 log G = 44.6 dB Approximating the antenna pattern as a rectangular area: The second term in the equation above is identical to equation [3]. For a very directional radar dish with a beamwidth of 1° and an average efficiency of 70%: Ideally (in dB form): 10 log G =10 log 41253 = 46.2 dB. With efficiency taken into account, G = 0.7(41253) = 28877, or in log form: 10 log G = 44.6 dB Comparison between elliptical and rectangular areas for antenna pattern models By using the rectangular model there is a direct correlation between the development of gain in equation [5] and the ideal gain of equation [3]. The elliptical model has about one dB difference from the ideal calculation, but will yield the same real antenna gain when appropriate efficiencies are assumed. The upper plot of Figure 4 shows the gain for an ideal antenna pattern using the elliptical model. The middle plot shows the gain for an ideal antenna using the rectangular model. The lower plot of Figure 4 shows the gain of a typical real antenna (rectangular model using an efficiency of 70%or elliptical model using an efficiency of 47%). Gain as a function of λ: When θ = 0, each wave source in Figure 5 is in phase with one another and a maximum is produced in that direction. Conversely, nulls to either side of the main lobe will occur when the waves radiating from the antenna cancel each other. The first null occurs when there is a phase difference of λ/2 in the wave fronts emanating from the aperture. To aid in visualizing what happens, consider each point in the antenna aperture, from A to C in Figure 5, as a point source of a spherical wave front. If viewed from infinity, the electromagnetic waves from each point interfere with each other, and when, for a particular direction, θ in Figure 5, each wave source has a corresponding point that is one-half wavelength out of phase, a null is produced in that direction due to destructive interference.
Sin θ = λ/L and, in radians, θ = λ/L (for small angles) [7] As the angle off boresight is increased beyond the first null, the intensity of the radiation pattern rises then falls, until the second null is reached. This corresponds to a phase difference of two wavelengths between the left and right edges of the aperture. In this case, the argument proceeds as before, except now the aperture is divided into four segments (point A canceling with a point halfway between A and B, and so on). The angle θ is the angle from the center (maximum) of the radiation pattern to the first null. The null-to-null beam width is 2θ. Generally, we are interested in the half-power (3 dB) beamwidth. It turns out that this beamwidth is approximately one-half of the null-to-null beamwidth, so that: BW3 dB = (½)(2θ) = λ/L [8] Therefore, beamwidth is a function of the antenna dimension “L” and the wavelength of the signal. It can be expressed as follows: Note: for circular antennas, L in the following equations = diameter
Substituting the two variations of equation [9] into equation [3] and since LAz eff times LEl eff = Ae (effective capture area of the antenna), we have:
Note: Equation is approximate since aperture efficiency isn't included as is done later in equation [12]. The efficiency (discussed later) will reduce the gain by a factor of 30-50%, i.e. real gain = .5 to .7 times theoretical gain. Unity Gain Antenna. If a square antenna is visualized and G=1, Ae = λ2/4π. When a dimension is greater than 0.28λ (~¼λ ) it is known as an electrically large antenna, and the antenna will have a gain greater than one (positive gain when expressed in dB). Conversely, when the dimension is less than 0.28λ (~¼λ )(an electrically small antenna), the gain will be less than one (negative gain when expressed in dB). Therefore, a unity gain antenna can be approximated by an aperture that is ¼λ by ¼λ. Beamwidth as a Function of Aperture Length It can be seen from Figure 5, that the wider the antenna aperture (L), the narrower the beamwidth will be for the same λ. Therefore, if you have a rectangular shaped horn antenna, the radiation pattern from the wider side will be narrower than the radiation pattern from the narrow side.
APERTURE EFFICIENCY, η The Antenna Efficiency, η, is a factor which includes all reductions from the maximum gain. η can be expressed as a percentage, or in dB. Several types of "loss" must be accounted for in the efficiency, η: (1) Illumination efficiency which is the ratio of the directivity of the antenna to the directivity of a uniformly illuminated antenna of the same aperture size, (2) Phase error loss or loss due to the fact that the aperture is not a uniform phase surface, (3) Spillover loss (Reflector Antennas) which reflects the energy spilling beyond the edge of the reflector into the back lobes of the antenna, (4) Mismatch (VSWR) loss, derived from the reflection at the feed port due to impedance mismatch (especially important for low frequency antennas), and (5) RF losses between the antenna and the antenna feed port or measurement point.
The aperture efficiency, ηa, is also known as the illumination factor, and includes items (1) and (2) above; it does not result in any loss of power radiated but affects the gain and pattern. It is nominally 0.6-0.8 for a planer array and 0.13 to 0.8 with a nominal value of 0.5 for a parabolic antenna, however η can vary significantly. Other antennas include the spiral (.002-.5), the horn (.002-.8), the double ridge horn (.005-.93), and the conical log spiral (.0017-1.0). Items (3), (4), and (5) above represent RF or power losses which can be measured. The efficiency varies and generally gets lower with wider bandwidths. Also note that the gain equation is optimized for small angles - see derivation of wavelength portion of equation [7]. This explains why efficiency also gets lower for wider beamwidth antennas.
EFFECTIVE CAPTURE AREA Effective capture area (Ae) is the product of the physical aperture area (A) and the aperture efficiency (η) or:
GAIN AS A FUNCTION OF APERTURE EFFICIENCY The Gain of an antenna with losses is given by:
Note that the gain is proportional to the aperture area and inversely proportional to the square of the wavelength. For example, if the frequency is doubled, (half the wavelength), the aperture could be decreased four times to maintain the same gain.
BEAM FACTOR Antenna size and beamwidth are also related by the beam factor defined by: Beam Factor = (D/λ)·(Beamwidth) where D = antenna dimension in wavelengths. The beam factor is approximately invariant with antenna size, but does vary with type of antenna aperture illumination or taper. The beam factor typically varies from 50-70°.
APERTURE ILLUMINATION (TAPER) The aperture illumination or illumination taper is the variation in amplitude across the aperture. This variation can have several effects on the antenna performance: (1) reduction in gain, (2) reduced (lower) sidelobes in most cases, and (3) increased antenna beamwidth and beam factor.
Tapered illumination occurs naturally in reflector antennas due to the feed radiation pattern and the variation in distance from the feed to different portions of the reflector. Phase can also vary across the aperture which also affects the gain, efficiency, and beamwidth.
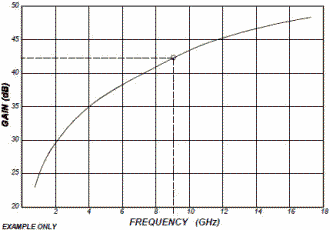
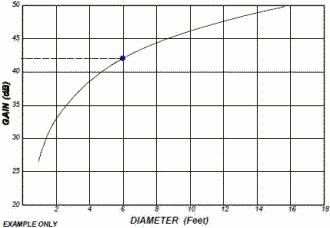
CIRCULAR ANTENNA GAIN Solving equation [12] in dB, for a circular antenna with area πDλ/4, we have: 10 Log G = 20 Log (D/λ) + 10 Log (η) + 9.94 dB ; where D = diameter [13] This data is depicted in the nomograph of Figure 6. For example, a six foot diameter antenna operating at 9 GHz would have approximately 44.7 dB of gain as shown by the dashed line drawn on Figure 6. This gain is for an antenna 100% efficient, and would be 41.7 dB for a typical parabolic antenna (50% efficient). An example of a typical antenna (with losses) showing the variation of gain with frequency is depicted in Figure 7, and the variation of gain with antenna diameter in Figure 8. The circle on the curves in Figure 7 and 8 correspond to the Figure 6 example and yields 42 dB of gain for the
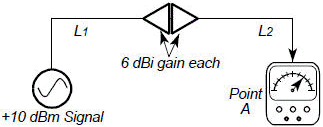
Figure 6. Antenna Gain Nomograph Example Problem: If the two antennas in the drawing are “welded” together, how much power will be measured at point A? (Line loss L1 = L2 = 0.5, and 10log L1 or L2 = 3 dB) Multiple choice: A. 16 dBm b. 28 dBm c. 4 dBm d. 10 dBm e. < 4 dBm
Answer: The antennas do not act as they normally would since the antennas are operating in the near field. They act as inefficient coupling devices resulting in some loss of signal. In addition, since there are no active components, you cannot end up with more power than you started with. The correct answer is “e. < 4 dBm.” 10 dBm - 3 dB - small loss -3 dB = 4 dBm - small loss If the antennas were separated by 5 ft and were in the far field, the antenna gain could be used with space loss formulas to calculate (at 5 GHz): 10 dBm - 3 dB + 6 dB - 50 dB (space loss) + 6 dB -3 dB = -34 dBm (a much smaller signal).
Figure 7. Gain of a Typical 6 Foot Dish Antenna (with Losses) Figure 8. Gain of a Typical Dish at 9 GHz (with Losses) Table of Contents for Electronics Warfare and Radar Engineering Handbook Introduction | Abbreviations | Decibel | Duty Cycle | Doppler Shift | Radar Horizon / Line of Sight | Propagation Time / Resolution | Modulation | Transforms / Wavelets | Antenna Introduction / Basics | Polarization | Radiation Patterns | Frequency / Phase Effects of Antennas | Antenna Near Field | Radiation Hazards | Power Density | One-Way Radar Equation / RF Propagation | Two-Way Radar Equation (Monostatic) | Alternate Two-Way Radar Equation | Two-Way Radar Equation (Bistatic) | Jamming to Signal (J/S) Ratio - Constant Power [Saturated] Jamming | Support Jamming | Radar Cross Section (RCS) | Emission Control (EMCON) | RF Atmospheric Absorption / Ducting | Receiver Sensitivity / Noise | Receiver Types and Characteristics | General Radar Display Types | IFF - Identification - Friend or Foe | Receiver Tests | Signal Sorting Methods and Direction Finding | Voltage Standing Wave Ratio (VSWR) / Reflection Coefficient / Return Loss / Mismatch Loss | Microwave Coaxial Connectors | Power Dividers/Combiner and Directional Couplers | Attenuators / Filters / DC Blocks | Terminations / Dummy Loads | Circulators and Diplexers | Mixers and Frequency Discriminators | Detectors | Microwave Measurements | Microwave Waveguides and Coaxial Cable | Electro-Optics | Laser Safety | Mach Number and Airspeed vs. Altitude Mach Number | EMP/ Aircraft Dimensions | Data Busses | RS-232 Interface | RS-422 Balanced Voltage Interface | RS-485 Interface | IEEE-488 Interface Bus (HP-IB/GP-IB) | MIL-STD-1553 & 1773 Data Bus | This HTML version may be printed but not reproduced on websites. Related Pages on RF Cafe - Antennas - Hardware & Controls - Antennas - Manufacturers & Services - Test Equipment & Calibration - Antenna Measurement - Antenna Introduction / Basics - Near-Field / Far-Field Transition Distance - Intro to Wave Propagation, Transmission Lines, Antennas - Antenna, Electromagnetics & X-mission Line Simulators |
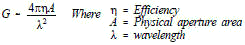

 3.
Gain of Circular X-Band Aperture
3.
Gain of Circular X-Band Aperture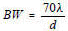
 The
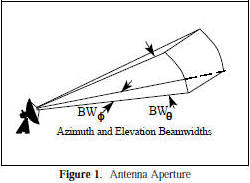
antenna equations which follow relate to Figure 1 as a typical antenna. In Figure 1, BWN is the azimuth beamwidth
and BW2 is the elevation beamwidth. Beamwidth is normally measured at the half-power or -3 dB point of the main
lobe unless otherwise specified. See Glossary.
The
antenna equations which follow relate to Figure 1 as a typical antenna. In Figure 1, BWN is the azimuth beamwidth
and BW2 is the elevation beamwidth. Beamwidth is normally measured at the half-power or -3 dB point of the main
lobe unless otherwise specified. See Glossary.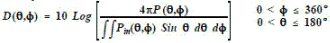
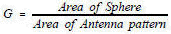 [2]
[2]


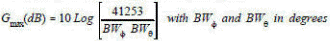
 In
Figure 5, the wave emanating from point A is out of phase with the wave from point B by one-half of a wavelength.
Hence, they cancel. Similarly, a point just to the right of point A cancels with a point just to the right of
point B, and so on across the entire aperture. Therefore, the first null in the radiation pattern is given by:
In
Figure 5, the wave emanating from point A is out of phase with the wave from point B by one-half of a wavelength.
Hence, they cancel. Similarly, a point just to the right of point A cancels with a point just to the right of
point B, and so on across the entire aperture. Therefore, the first null in the radiation pattern is given by: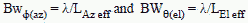 [9]
[9]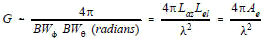 [10]
[10]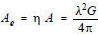 [11]
[11]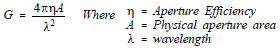 [12]
[12]