Electronic Warfare and Radar Systems Engineering Handbook |
|
RECEIVER SENSITIVITY / NOISE RECEIVER SENSITIVITY Sensitivity in a receiver is normally taken as the minimum input signal (Smin) required to produce a specified output signal having a specified signal-to-noise (S/N) ratio and is defined as the minimum signal-to-noise ratio times the mean noise power, see equation [1]. For a signal impinging on the antenna (system level) sensitivity is known as minimum operational sensitivity (MOS), see equation [2]. Since MOS includes antenna gain, it may be expressed in dBLi (dB referenced to a linear isotropic antenna). When specifying the sensitivity of receivers intended to intercept and process pulse signals, the minimum pulse width at which the specified sensitivity applies must also be stated. See the discussion of post-detection bandwidth (BV) in Section 5-2 for significance of minimum pulse width in the receiver design. Smin = (S/N)minkToB(NF) receiver sensitivity ("black box" performance parameter) [1] or MOS = (S/N)minkToB(NF)/G system sensitivity i.e. the receiver is connected to an antenna [2]
(transmission line loss included with antenna gain) where: S/Nmin = Minimum signal-to-noise ratio needed to process (vice just detect) a signal
NF = Noise figure/factor k = Boltzmann's Constant = 1.38 x 10-23 Joule/°K To = Absolute temperature of the receiver input (°Kelvin) = 290°K B = Receiver Bandwidth (Hz) G = Antenna/system gain We have a lower MOS if temperature, bandwidth, NF, or S/Nmin decreases, or if antenna gain increases. For radar, missile, and EW receivers, sensitivity is usually stated in dBm. For communications and commercial broadcasting receivers, sensitivity is usually stated in micro-volts or dBμv. See Section 4-1. There is no standard definition of sensitivity level. The term minimum operational sensitivity (MOS) can be used in place of Smin at the system level where aircraft installation characteristics are included. The "black box" term minimum detectable signal (MDS) is often used for Smin but can cause confusion because a receiver may be able to detect a signal, but not properly process it. MDS can also be confused with minimum discernable signal, which is frequently used when a human operator is used to interpret the reception results. A human interpretation is also required with minimum visible signal (MVS) and tangential sensitivity (discussed later). To avoid confusion, the terms Smin for "black box" minimum sensitivity and MOS for system minimum sensitivity are used in this section. All receivers are designed for a certain sensitivity level based on requirements. One would not design a receiver with more sensitivity than required because it limits the receiver bandwidth and will require the receiver to process signals it is not interested in. In general, while processing signals, the higher the power level at which the sensitivity is set, the fewer the number of false alarms which will be processed. Simultaneously, the probability of detection of a "good" (low-noise) signal will be decreased. Sensitivity can be defined in two opposite ways, so discussions can frequently be confusing. It can be the ratio of response to input or input to response. In using the first method (most common in receiver discussions and used herein), it will be a negative number (in dBm), with the more negative being "better" sensitivity, e.g. -60 dBm is "better" than -50 dBm sensitivity. If the second method is used, the result will be a positive number, with higher being "better." Therefore the terms low sensitivity or high sensitivity can be very confusing. The terms Smin and MOS avoid confusion.
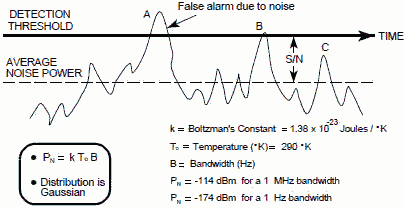
SIGNAL-TO-NOISE (S/N) RATIO The Signal-to-Noise Ratio (S/N) (a.k.a. SNR) in a receiver is the signal power in the receiver divided by the mean noise power of the receiver. All receivers require the signal to exceed the noise by some amount. Usually if the signal power is less than or just equals the noise power it is not detectable. For a signal to be detected, the signal energy plus the noise energy must exceed some threshold value. Therefore, just because N is in the denominator doesn't mean it can be increased to lower the MOS. S/N is a required minimum ratio, if N is increased, then S must also be increased to maintain that threshold. The threshold value is chosen high enough above the mean noise level so that the probability of random noise peaks exceeding the threshold, and causing false alarms, is acceptably low. Figure 1 depicts the concept of required S/N. It can be seen that the signal at time A exceeds the S/N ratio and indicates a false alarm or target. The signal at time B is just at the threshold, and the signal at time C is clearly below it. In the sample, if the temperature is taken as room temperature (To = 290EK), the noise power input is -114 dBm for a one MHz bandwidth. Normally S/Nmin may be set higher than S/N shown in Figure 1 to meet false alarm specifications.
Figure 1. Receiver Noise Power at Room Temperature The acceptable minimum Signal-to-Noise ratio (or think of it as Signal above Noise) for a receiver depends on the intended use of the receiver. For instance, a receiver that had to detect a single radar pulse would probably need a higher minimum S/N than a receiver that could integrate a large number of radar pulses (increasing the total signal energy) for detection with the same probability of false alarms. Receivers with human operators using a video display may function satisfactorily with low minimum S/N because a skilled operator can be very proficient at picking signals out of a noise background. As shown in Table 1, the setting of an acceptable minimum S/N is highly dependant on the required characteristics of the receiver and of the signal.
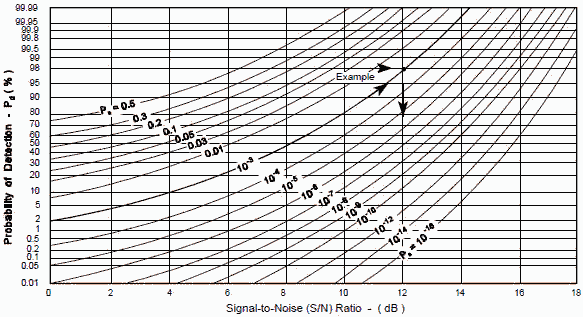
Skilled Operator Auto-Detection TOA, and Frequency Measurements Interferometer Comparison Auto-detection with Amplitude, AOA Phase AOA Amplitude 3 to 8 dB 10 to 14 dB 14 to 18 dB 14 to 18 dB 16 to 24 dB A complete discussion of the subject would require a lengthy dissertation of the probability and statistics of signal detection, which is beyond the scope of this handbook, however a simplified introduction follows. Let's assume that we have a receiver that we want a certain probability of detecting a single pulse with a specified false alarm probability. We can use Figure 2 to determine the required signal-to-noise ratio.
S/N EXAMPLE If we are given that the desired probability of detecting a single pulse (Pd) is 98%, and we want the false alarm rate (Pn) to be no more than 10 , then we can see that S/N must be 12 dB (see Figure 2).
Figure 2. Nomograph of Signal-to-Noise (S/N) Ratio as a Function of Probability of Detection (Pd) and Probability of False Alarm Rate (Pn)
MAXIMUM DETECTION RANGE (ONE-WAY) From Section 4-3, the one way signal strength from a transmitter to a receiver is: For calculations involving receiver sensitivity the "S" can be replaced by Smin. Since Smin = (S/N)min kToB(NF), given by equation [1], the one-way radar equation can be solved for any of the other variables in terms of receiver parameters. In communication, radar, and electronic warfare applications, you might need to solve for the maximum range (Rmax) where a given radar warning receiver could detect a radiated signal with known parameters. We would then combine and rearrange the two equations mentioned to solve for the following one-way equation:
We could use standard room temperature of 290° K as To, but NF would have to be determined as shown later. In this calculation for receiver Rmax determination, Pt , Gt , and λ are radar dependent, while Gr , S/Nmin, NF, and B are receiver dependent factors. Equation [3] relates the maximum detection range to bandwidth (B). The effects of the measurement bandwidth can significantly reduce the energy that can be measured from the peak power applied to the receiver input. Additional bandwidth details are provided in Sections 4-4, 4-7, and in other parts of this section NOISE POWER, kToB
Thermal noise is spread more or less uniformly over the entire frequency spectrum. Therefore the amount of noise appearing in the output of an ideal receiver is proportional to the absolute temperature of the receiver input system (antenna etc) times the bandwidth of the receiver. The factor of proportionality is Boltzmann's Constant. Mean noise power of ideal receiver = kToB = PN (Watts) Mean noise power of a real receiver = (NF)kToB (Watts) The convention for the temperature of To is set by IEEE standard to be 290°K, which is close to ordinary room temperature. So, assuming To = 290°K, and for a bandwidth B = 1 Hz, kToB = 4x10-21 W = -204 dBW = -174 dBm. For any receiver bandwidth, multiply 4x10-21 W by the bandwidth in Hz, or if using dB; 10 log kToB = -174 dBm + 10 Log (actual Bandwidth in Hz) or -114 dBm + 10 Log (actual Bandwidth in MHz) and so on, as shown by the values in Table 2. Typical values for maximum sensitivity of receivers would be: RWR -65 dBm Pulse Radar -94 dBm CW Missile Seeker -138 dBm If antenna contributions are ignored (see note in Table 4) for a CW receiver with a 4 GHz bandwidth, the ideal mean noise power would be -174 dBm + 10 Log(4x109) = -174 dBm + 96 dB = -78 dBm. A skilled operator might only be able to distinguish a signal 3 dB above the noise floor (S/N=3 dB), or -75 dBm. A typical radar receiver would require a S/N of 3 to 10 dB to distinguish the signal from noise, and would require 10 to 20 dB to track. Auto tracking might require a S/N of approximately 25 dB, thus, a receiver may only have sufficient sensitivity to be able to identify targets down to -53 dBm. Actual pulse receiver detection will be further reduced due to sin x/x frequency distribution and the effect of the measurement bandwidth as discussed in Sections 4-4 and 4-7. Integration will increase the S/N since the signal is coherent and the noise is not.
Noise Bandwidth Equivalent Noise Bandwidth (BN) - Set by minimum pulse width or maximum modulation bandwidth needed for the system requirements. A choice which is available to the designer is the relationship of pre- and post-detection bandwidth. Pre-detection bandwidth is denoted by BIF , while post-detection is denoted BV , where V stands for video. The most affordable approach is to set the post-detection filter equal to the reciprocal of the minimum pulse width, then choose the pre-detection passband to be as wide as the background interference environment will allow. Recent studies suggest that pre-detection bandwidths in excess of 100 MHz will allow significant loss of signals due to "pulse-on-pulse" conditions. Equations [4] and [5] provide BN relationships that don't follow the Table 3 rules of thumb.
T For a square law detector: (1) At high (S/N)out, the 1/(S/Nout)
term goes to zero and we have: At low (S/N)out, the 1/(S/Nout) term dominates, and we have:
For a linear detector: (1) H is a hypergeometric (statistical) function of (S/N)in H = 2 for (S/N)in << 1 H = 1 for (S/N)in >> 1 At high (S/N)out, the 1/(S/Nout) term goes to zero and we have: At low (S/N)out, the 1/(S/Nout) term dominates, and we have:
Note (1): From Klipper, Sensitivity of crystal Video Receivers with RF Pre-amplification, The Microwave Journal, August 1965.
TRADITIONAL "RULE OF THUMB" FOR NARROW BANDWIDTHS (Radar Receiver Applications) Required IF Bandwidth For Matched Filter Applications:
Matched filter performance gives maximum probability of detection for a given signal level, but: (1) Requires perfect centering of signal spectrum with filter bandwidth, (2) Time response of matched pulse does not stabilize at a final value, and (3) Out-of-band splatter impulse duration equals minimum pulse width. As a result, EW performance with pulses of unknown frequency and pulse width is poor.
Some authors define BV in terms of the minimum rise time of the detected pulse, i.e., BV = (0.35 to 0.5)/tr min, where tr = rise time. REVISED "RULE OF THUMB" FOR WIDE BANDWIDTHS (Wideband Portion of RWRs)
The pre-detection bandwidth is chosen based upon interference and spurious generation concerns. The post-detection bandwidth is chosen to "match" the minimum pulse width. This allows (1) Half bandwidth mistuning between signal and filter, (2) Half of the minimum pulse width for final value stabilization, and (3) The noise bandwidth to be "matched" to the minimum pulse width. As a result, there is (1) Improved EW performance with pulses of unknown frequency and pulse width, (2) Measurement of in-band, but mistuned pulses, and (3) Rejection of out-of-band pulse splatter.
NOISE FIGURE / FACTOR (NF) Electrical noise is defined as electrical energy of random amplitude, phase, and frequency. It is present in the output of every radio receiver. At the frequencies used by most radars, the noise is generated primarily within the input stages of the receiver system itself (Johnson Noise). These stages are not inherently noisier than others, but noise generated at the input and amplified by the receiver's full gain greatly exceeds the noise generated further along the receiver chain. The noise performance of a receiver is described by a figure of merit called the noise figure (NF). The term noise factor is synonymous, with some authors using the term "factor" for numeric and "figure" when using dB notation. (The notation "Fn" is also sometimes used instead of "NF".) The noise figure is defined as:
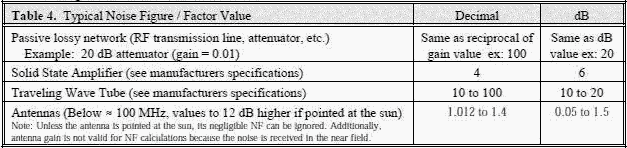
A range of NF values is shown in Table 4.
An ideal receiver generates no noise internally. The only noise in its output is received from external sources. That noise has the same characteristics as the noise resulting from thermal agitation in a conductor. Thermal agitation noise is caused by the continuous random motion of free electrons which are present in every conductor. The amount of motion is proportional to the conductor's temperature above absolute zero. For passive lossy networks, the noise factor equals the loss value for the passive element:
A typical series of cascaded amplifiers is shown in Figure 3.
Figure 3. Noise Factors for Cascaded Amplifiers (NFCA) Loss (negative gain) can be used for the gain value of attenuators or transmission line loss, etc to calculate the noise out of the installation as shown in the following equation:
If the bandwidths of the amplifiers are the same, equation [6] becomes:
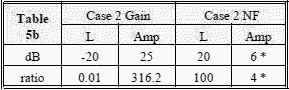
For this example, case 2 has a noise level at the input to the receiver which is 19.7 dB higher than case 1 (calculations follow later).
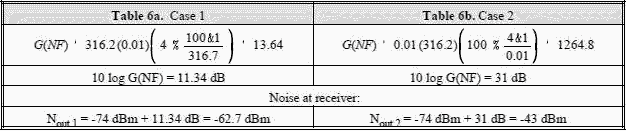
Using equation [3] and the data in Tables 5a and 5b, the noise generated by the RF installation is shown in Tables 6a and 6b (the negligible noise contribution from the antenna is the same in both cases and is not included) (also see notes contained in Table 4):
Nout 2 - Nout 1 = 19.7 dB. The input noise of -74 dBm was calculated using 10 log (kTB), where B = 10 GHz. Note that other tradeoffs must be considered: (1) greater line loss between the antenna and amplifier improves (decreases) VSWR as shown in Section 6-2, and (2) the more input line loss, the higher the input signal can be before causing the pre-amplifier to become saturated (mixing of signals due to a saturated amplifier is addressed in Section 5-7).
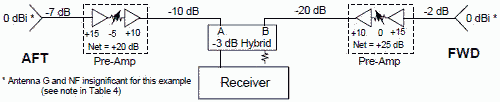
Combining Receive Paths Can Reduce Sensitivity If a single aircraft receiver processes both forward and aft signals as shown in Figure 5, it is desirable o be able to use the receiver's full dynamic range for both directions. Therefore, one needs to balance the gain, so that a signal applied to the aft antenna will reach the receiver at the same level as if it was applied to the forward antenna.
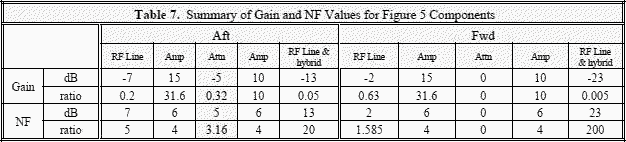
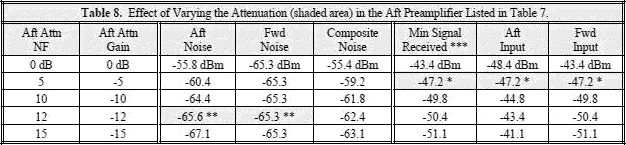
Figure 5. Example of Pre-Amplifier Affecting Overall Gain/Sensitivity Common adjustable preamplifiers can be installed to account for the excessive transmission line loss. In this example, in the forward installation, the level of the signal at the receiver is the same as the level applied to the antenna. Since the aft transmission line has 5 dB less attenuation, that amount is added to the preamplifier attenuator to balance the gain. This works fine for strong signals, but not for weaker signals. Because there is less loss between the aft preamplifier and the receiver, the aft noise dominates and will limit forward sensitivity. If the bandwidth is 2-12 GHz, and if port A of the hybrid is terminated by a perfect 50S load, the forward noise level would be -65.3 dBm. If port B is terminated, the aft noise level would be -60.4 dBm. With both ports connected, the composite noise level would be -59.2 dBm (convert to mw, add, then convert back to dBm). For this example, if the aft preamplifier attenuation value is changed to 12 dB, the gain is no longer balanced (7 dB extra loss aft), but the noise is balanced, i.e. forward = -65.6 dBm, aft = -65.3 dBm, and composite -62.4 dBm. If there were a requirement to see the forward signals at the most sensitive level, extra attenuation could be inserted in the aft preamplifier. This would allow the forward noise level to predominate and result in greater forward sensitivity where it is needed. Calculations are provided in Tables 7 and 8.
Aft NF = 22.79 therefore 10 log NF = 13.58 dB. Input noise level = -74 dBm + 13.58 dB ≈ -60.42 dBm -60.4 dBm Fwd NF = 7.495 therefore 10 log NF = 8.75 dB. Input noise level = -74 dBm + 8.75 dB ≈ -65.25 dBm -65.3 dBm The composite noise level at the receiver = -59.187 dBm ≈ -59.2 dBm
* Gain Balanced ** Noise Balanced *** S/N was set at 12 dB
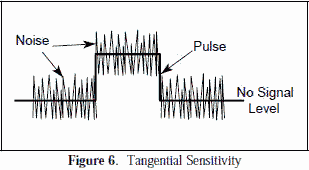
Tangential sensitivity (TSS) is the point where the top of the noise level with no signal applied is level with the bottom of the noise level on a pulse as shown in Figure 6. It can be determined in the laboratory by varying the amplitude of the input pulse until the stated criterion is reached, or by various approximation formulas. The signal power is nominally 8±1 dB above the noise level at the TSS point. TSS depends on the RF bandwidth, the video bandwidth, the noise figure, and the detector characteristic. TSS is generally a characteristic associated with receivers (or RWRs), however the TSS does not necessarily provide a criterion for properly setting the detection threshold. If the threshold is set to TSS, then the false alarm rate is rather high. Radars do not operate at TSS. Most require a more positive S/N for track ( > 10 dB) to reduce false detection on noise spikes.
SENSITIVITY CONCLUSION When all factors effecting system sensitivity are considered, the designer has little flexibility in the choice of receiver parameters. Rather, the performance requirements dictate the limit of sensitivity which can be implemented by the EW receiver. 1. Minimum Signal-to-Noise Ratio (S/N) - Set by the accuracy which you want to measure signal parameters and by the false alarm requirements. 2. Total Receiver Noise Figure (NF) - Set by available technology and system constraints for RF front end performance. 3. Equivalent Noise Bandwidth (BN) - Set by minimum pulse width or maximum modulation bandwidth needed to accomplish the system requirements. A choice which is available to the designer is the relationship of pre- (BIF) and post-detection (BV) bandwidth. The most affordable approach is to set the post-detection filter equal to the reciprocal of the minimum pulse width, then choose the pre-detection passband to be as wide as the background interference environment will allow. Recent studies suggest that pre-detection bandwidths in excess of 100 MHz will allow significant loss of signals due to "pulse-on-pulse" conditions. 4. Antenna Gain (G) - Set by the needed instantaneous FOV needed to support the system time to intercept requirements.
Table of Contents for Electronics Warfare and Radar Engineering Handbook Introduction | Abbreviations | Decibel | Duty Cycle | Doppler Shift | Radar Horizon / Line of Sight | Propagation Time / Resolution | Modulation | Transforms / Wavelets | Antenna Introduction / Basics | Polarization | Radiation Patterns | Frequency / Phase Effects of Antennas | Antenna Near Field | Radiation Hazards | Power Density | One-Way Radar Equation / RF Propagation | Two-Way Radar Equation (Monostatic) | Alternate Two-Way Radar Equation | Two-Way Radar Equation (Bistatic) | Jamming to Signal (J/S) Ratio - Constant Power [Saturated] Jamming | Support Jamming | Radar Cross Section (RCS) | Emission Control (EMCON) | RF Atmospheric Absorption / Ducting | Receiver Sensitivity / Noise | Receiver Types and Characteristics | General Radar Display Types | IFF - Identification - Friend or Foe | Receiver Tests | Signal Sorting Methods and Direction Finding | Voltage Standing Wave Ratio (VSWR) / Reflection Coefficient / Return Loss / Mismatch Loss | Microwave Coaxial Connectors | Power Dividers/Combiner and Directional Couplers | Attenuators / Filters / DC Blocks | Terminations / Dummy Loads | Circulators and Diplexers | Mixers and Frequency Discriminators | Detectors | Microwave Measurements | Microwave Waveguides and Coaxial Cable | Electro-Optics | Laser Safety | Mach Number and Airspeed vs. Altitude Mach Number | EMP/ Aircraft Dimensions | Data Busses | RS-232 Interface | RS-422 Balanced Voltage Interface | RS-485 Interface | IEEE-488 Interface Bus (HP-IB/GP-IB) | MIL-STD-1553 & 1773 Data Bus | This HTML version may be printed but not reproduced on websites. |

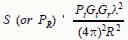
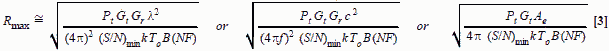

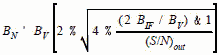 [4]
[4]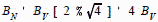
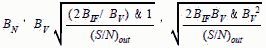
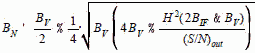 [5]
[5]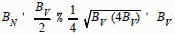
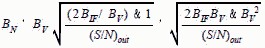
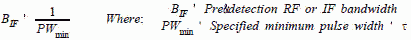
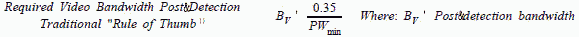
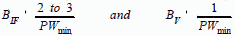
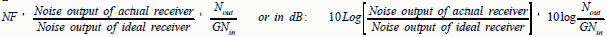
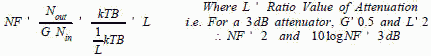

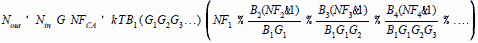 (ratio form)
[6]
(ratio form)
[6]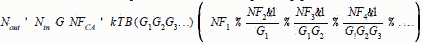 (ratio form) [7]
(ratio form) [7]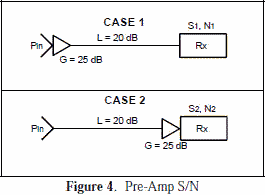 Pre-amplifier Location
Affects Receiver Input Noise As shown in Figure 4, if a 2 to 12 GHz receiver installation doesn't have enough sensitivity, it is best to install
an additional amplifier closer to the antenna (case 1) instead of closer to the receiver (case 2). In both cases, the line loss (L) and the
amplifier gain (G) are the same, so the signal level at the receiver is the same. The noise generated by the passive transmission line when
measured at the receiver is the same in both cases. However, the noise generated inside the amplifier, when measured at the receiver input,
is different.
Pre-amplifier Location
Affects Receiver Input Noise As shown in Figure 4, if a 2 to 12 GHz receiver installation doesn't have enough sensitivity, it is best to install
an additional amplifier closer to the antenna (case 1) instead of closer to the receiver (case 2). In both cases, the line loss (L) and the
amplifier gain (G) are the same, so the signal level at the receiver is the same. The noise generated by the passive transmission line when
measured at the receiver is the same in both cases. However, the noise generated inside the amplifier, when measured at the receiver input,
is different.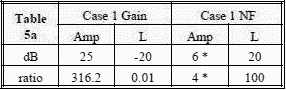
 TANGENTIAL SENSITIVITY
TANGENTIAL SENSITIVITY