Electronic Warfare and Radar Systems Engineering Handbook
|
||
|
Doppler Shift Doppler is the apparent change in wavelength (or frequency) of an electromagnetic or acoustic wave when there is relative movement between the transmitter (or frequency source) and the receiver.
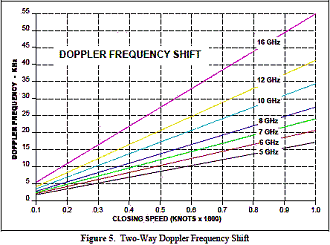
To estimate fD at other frequencies, multiply these by:
How do we know the universe is expanding? Answer: The color of light from distant stars is shifted to red (see Section 7-1: higher 8 or lower frequency means Doppler shift is stretched, i.e. expanding). A memory aid might be that the lights from a car (going away) at night are red (tail lights)!
* Transmitter in motion * Reflector in motion * Receiver in motion * All three For a closing relative velocity:* Wave is compressed * Frequency is increased For an opening relative velocity:* Wave is stretched * Frequency is decreased To compute Doppler frequency we note that velocity is range rate; V = dr/dt
When the 2nd peak reaches the target, the target has advanced according to its velocity (vt) (point b), and the first reflected peak has traveled toward the radar by an amount that is less than the original wavelength by the same amount (vt) (point c). As the 2nd peak is reflected, the wavelength of the reflected wave is 2(vt) less than the original wavelength (point d). The distance the wave travels is twice the target range. The reflected phase lags transmitted phase by 2x the round trip time. For a fixed target the received phase will differ from the transmitted phase by a constant phase shift. For a moving target the received phase will differ by a changing phase shift. For the closing target shown in Figure 3, the received phase is advancing with respect to the transmitted phase and appears as a higher frequency.
For the following equations (except radar mapping), we assume the radar and target are moving directly toward one another in order to simplify calculations (if this is not the case, use the velocity component of one in the direction of the other in the formulas). For the case of a moving reflector, Doppler frequency is proportional to 2x the transmitted frequency: Higher rf = higher Doppler shift fD = (2 x VTarget)(f/c) Likewise, it can be shown that for other cases, the following relationships hold:
fD = 2(VRadar + VTarget)(f/c) For the case of a semi-active missile receiving signals (Also "all three moving") fD = (VRadar + 2VTarget +VMissile)(f/c) For the airplane radar with a ground target (radar mapping) or vice versa. fD = 2(VRadar Cosθ Cosф)(f/c), Where 2 and N are the radar scan azimuth and depression angles. For a ground based radar with airborne target - same as previous using target track crossing angle and ground radar elevation angle. For the ES/ESM/RWR case where only the target or receiver is moving (One-way Doppler measurements) fD = VReceiver or Target (f/c) Note: See Figure 4 if radar and target are not moving directly towards or away from one another.
Sample Problems: (1) If a ground radar operating at 10 GHz is tracking an airplane flying at a speed of 500 km/hr tangential to it (crossing pattern) at a distance of 10 km, what is the Doppler shift of the returning signal? Answer: Since the closing velocity is zero, the Doppler is also zero. (2) If the same aircraft turns directly toward the ground radar, what is the Doppler shift of the returning signal? Answer: 500 km/hr = 270 kts from Section 2-1. From Figure 4 we see that the Doppler frequency is about 9.2 kHz. (3) Given that a ground radar operating at 7 GHz is Doppler tracking an aircraft 20 km away (slant range) which is flying directly toward it at an altitude of 20,000 ft and a speed of 800 ft/sec, what amount of VGPO switch would be required of the aircraft jammer to deceive (pull) the radar to a zero Doppler return? Answer: We use the second equation from the bottom of page 2-6.3 which is essentially the same for this application except a ground based radar is tracking an airplane target (versus an airplane during ground mapping), so for our application we use a positive elevation angle instead of a negative (depression) angle. fD = 2(Vr Cos θ Cos ф)(f/c), where θ is the aircraft track crossing angle and ф is the radar elevation angle. Since the aircraft is flying directly at the radar, 2 = θ°; the aircraft altitude = 20,000 ft = 6,096 meters. Using the angle equation in Section 2-1, sin ф = x/r = altitude / slant range, so: ф = sin-1 (altitude/slant range) = sin-1 (6,096 m / 20,000 m) = 17.7° FD = 2(800 ft/sec Cos θ° Cos 17.7°)(7x10 Hz9 / 9.8357 x 109 ft/sec) = 10,845 Hz
Table of Contents for Electronics Warfare and Radar Engineering Handbook Introduction | Abbreviations | Decibel | Duty Cycle | Doppler Shift | Radar Horizon / Line of Sight | Propagation Time / Resolution | Modulation | Transforms / Wavelets | Antenna Introduction / Basics | Polarization | Radiation Patterns | Frequency / Phase Effects of Antennas | Antenna Near Field | Radiation Hazards | Power Density | One-Way Radar Equation / RF Propagation | Two-Way Radar Equation (Monostatic) | Alternate Two-Way Radar Equation | Two-Way Radar Equation (Bistatic) | Jamming to Signal (J/S) Ratio - Constant Power [Saturated] Jamming | Support Jamming | Radar Cross Section (RCS) | Emission Control (EMCON) | RF Atmospheric Absorption / Ducting | Receiver Sensitivity / Noise | Receiver Types and Characteristics | General Radar Display Types | IFF - Identification - Friend or Foe | Receiver Tests | Signal Sorting Methods and Direction Finding | Voltage Standing Wave Ratio (VSWR) / Reflection Coefficient / Return Loss / Mismatch Loss | Microwave Coaxial Connectors | Power Dividers/Combiner and Directional Couplers | Attenuators / Filters / DC Blocks | Terminations / Dummy Loads | Circulators and Diplexers | Mixers and Frequency Discriminators | Detectors | Microwave Measurements | Microwave Waveguides and Coaxial Cable | Electro-Optics | Laser Safety | Mach Number and Airspeed vs. Altitude Mach Number | EMP/ Aircraft Dimensions | Data Busses | RS-232 Interface | RS-422 Balanced Voltage Interface | RS-485 Interface | IEEE-488 Interface Bus (HP-IB/GP-IB) | MIL-STD-1553 & 1773 Data Bus | This HTML version may be printed but not reproduced on websites. Related Pages on RF Cafe - Introduction to Radar (Air University) - Radar Equation, 2-Way (another) - Radar Techniques - Primer (1945 QST) - RF Cafe Quiz #7 - Radar Principles - EW/Radar Handbook - Doppler Shift - Identification Friend or Foe (IFF) |
||
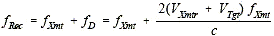
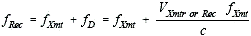
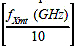
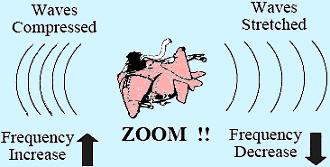 The Doppler effect is shown in Figure 1. In
everyday life this effect is commonly noticeable when a whistling train or police
siren passes you. Audio Doppler is depicted, however Doppler can also affect the
frequency of a radar carrier wave, the PRF of a pulse radar signal, or even light
waves causing a shift of color to the observer.
The Doppler effect is shown in Figure 1. In
everyday life this effect is commonly noticeable when a whistling train or police
siren passes you. Audio Doppler is depicted, however Doppler can also affect the
frequency of a radar carrier wave, the PRF of a pulse radar signal, or even light
waves causing a shift of color to the observer.
 For
the reflector in motion case, You can see the wave compression effect in Figure
3 when the transmitted wave peaks are one wavelength apart. When the first peak
reaches the target, they are still one wavelength apart (point a).
For
the reflector in motion case, You can see the wave compression effect in Figure
3 when the transmitted wave peaks are one wavelength apart. When the first peak
reaches the target, they are still one wavelength apart (point a).
 For an airplane radar
with an airplane target (The "all three moving" case)
For an airplane radar
with an airplane target (The "all three moving" case)