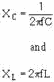NEETS Module 9 − Introduction to Wave− Generation and Wave−Shaping
Pages i,
1−1,
1−11,
1−21,
1−31,
1−41,
2−1,
2−11,
2−21,
2−31,
3−1,
3−11,
3−21,
3−31,
3−41,
3−51,
4−1,
4−11,
4−21,
4−31,
4−41,
4−51, Index
| - |
Matter, Energy,
and Direct Current |
| - |
Alternating Current and Transformers |
| - |
Circuit Protection, Control, and Measurement |
| - |
Electrical Conductors, Wiring Techniques,
and Schematic Reading |
| - |
Generators and Motors |
| - |
Electronic Emission, Tubes, and Power Supplies |
| - |
Solid-State Devices and Power Supplies |
| - |
Amplifiers |
| - |
Wave-Generation and Wave-Shaping Circuits |
| - |
Wave Propagation, Transmission Lines, and
Antennas |
| - |
Microwave Principles |
| - |
Modulation Principles |
| - |
Introduction to Number Systems and Logic Circuits |
| - |
- Introduction to Microelectronics |
| - |
Principles of Synchros, Servos, and Gyros |
| - |
Introduction to Test Equipment |
| - |
Radio-Frequency Communications Principles |
| - |
Radar Principles |
| - |
The Technician's Handbook, Master Glossary |
| - |
Test Methods and Practices |
| - |
Introduction to Digital Computers |
| - |
Magnetic Recording |
| - |
Introduction to Fiber Optics |
| Note: Navy Electricity and Electronics Training
Series (NEETS) content is U.S. Navy property in the public domain. |
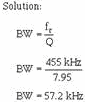
The Q of the circuit can be determined by transposing the formula for bandwidth to:
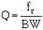
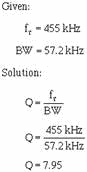
To find the Q of the circuit using the information found in the last example problem:
Q-12. What is the relationship of the coil to the resistance of a circuit with high "Q"?
Q-13. What is the band of frequencies called that is included between the two points at which current falls to
70 percent of its maximum value in a resonant circuit?
FILTERS In many practical applications of complex circuits, various combinations of direct, low-frequency,
audio-frequency, and radio-frequency currents may exist. It is frequently necessary to have a means for separating
these component currents at any desired point. An electrical device for accomplishing this separation is called a
FILTER. A filter circuit consists of inductance, capacitance, and resistance used singularly or in
combination, depending upon the purpose. It may be designed so that it will separate alternating current from
direct current, or so that it will separate alternating current of one frequency (or a band of frequencies) from
other alternating currents of different frequencies.
1-31
The use of resistance by itself in filter circuits does not provide any filtering action, because it
opposes the flow of any current regardless of its frequency. What it does, when connected in series or parallel
with an inductor or capacitor, is to decrease the "sharpness," or selectivity, of the filter. Hence, in some
particular application, resistance might be used in conjunction with inductance or capacitance to provide
filtering action over a wider band of frequencies. Filter circuits may be divided into four general types:
Low-PASS, High-PASS, Bandpass, and Band-REJECT filters. Electronic circuits often have currents of
different frequencies. The reason is that a source produces current with the same frequency as the applied
voltage. As an example, the AC signal input to an audio amplifier can have high- and low-audio frequencies; the
input to an RF amplifier can have a wide range of radio frequencies. In such applications where the
current has different frequency components, it is usually necessary for the filter either to accept or reject one
frequency or a group of frequencies. The electronic filter that can pass on the higher-frequency components to a
load or to the next circuit is known as a High-PASS filter. a Low-PASS filter can be used to pass on
lower-frequency components. Before discussing filters further, we will review and apply some basic
principles of the frequency- response characteristics of the capacitor and the inductor. Recall the basic formula
for capacitive reactance and inductive reactance:
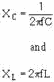 Assume any given value of L and C. If we increase the applied frequency, XC decreases and XL
increases. If we increase the frequency enough, the capacitor acts as a short and the inductor acts as an open. Of
course, the opposite is also true. Decreasing frequency causes XC to increase and XL to
decrease. Here again, if we make a large enough change, XC acts as an open and XL
acts as a short. Figure 1-13 gives a pictorial representation of these two basic components and how they respond
to low and high frequencies.
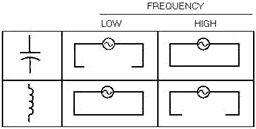
Figure 1-13. - Effect of frequency on capacitive and inductive reactance. 1-32
If we apply these same principles to simple circuits, such as the ones in figure 1-14, they affect
input signals as shown. For example, in view (A) of the figure, a low frequency is blocked by the capacitor which
acts as an open and at a high frequency the capacitor acts as a short. By studying the figure, it is easy to see
how the various components will react in different configurations with a change in frequency.
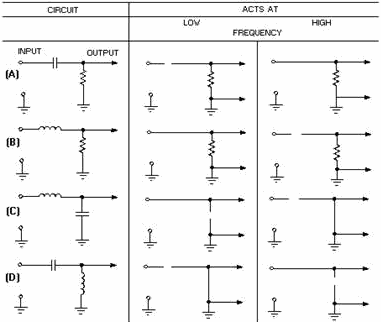
Figure 1-14. - Reaction to circuit by change in frequency. As mentioned before, high-pass and low-pass filters pass the specific frequencies for which circuits
are designed. There can be a great deal of confusion when talking about high-pass, low-pass,
discrimination, attenuation, and frequency cutoff, unless the terms are clearly understood. Since these terms are used widely throughout electronics texts and references, you should have a clear understanding before proceeding
further.
· High-PASS FILTER. a high-pass filter passes on a majority of the high frequencies to the next
circuit and rejects or attenuates the lower frequencies. Sometimes it is called a low-frequency discriminator or
low-frequency attenuator.
· Low-PASS FILTER. a low-pass filter passes on a majority of the low frequencies to the next circuit and rejects
or attenuates the higher frequencies. Sometimes it is called a high-frequency discriminator or high-frequency
attenuator.
1-33
· DIsCRIMINATION. The ability of the filter circuit to distinguish between high and low frequencies and to
eliminate or reject the unwanted frequencies.
· ATTENUATION. The ability of the filter circuit to reduce
the amplitude of the unwanted frequencies below the level of the desired output frequency.
· Frequency CUTofF (fco). The frequency at which the filter circuit changes from the point of
rejecting the unwanted frequencies to the point of passing the desired frequency; OR the point at which the filter
circuit changes from the point of passing the desired frequency to the point of rejecting the undesired
frequencies.
Low-PASS FILTER A low-pass filter passes all currents having a frequency below a
specified frequency, while opposing all currents having a frequency above this specified frequency. This action is
illustrated in its ideal form in view (A) of figure 1-15. At frequency cutoff, known as fc the current
decreases from maximum to zero. At all frequencies above fc the filter presents infinite opposition
and there is no current. However, this sharp division between no opposition and full opposition is impossible to
attain. a more practical graph of the current is shown in view (B), where the filter gradually builds up
opposition as the cutoff frequency (f) is approached. Notice that the filter cannot completely block current above
the cutoff frequency.
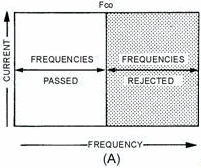
Figure 1-15A. - Low-pass filter.
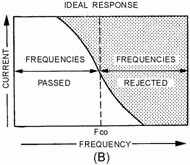
Figure 1-15B. - Low-pass filter.
1-34
View (A) of figure 1-16 shows the electrical construction of a low-pass filter with an inductor
inserted in series with one side of a line carrying both low and high frequencies. The opposition offered by the
reactance will be small at the lower frequencies and great at the higher frequencies. In order to divert the
undesired high frequencies back to the source, a capacitor must be added across the line to bypass the higher
frequencies around the load, as shown in view (B).
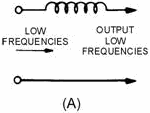
Figure 1-16A. - Components of a simple low-pass filter.
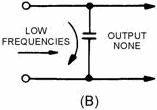
Figure 1-16B. - Components of a simple low-pass filter.
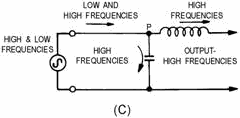
Figure 1-16C. - Components of a simple low-pass filter. The capacitance of the capacitor must be such that its reactance will offer little opposition to
frequencies above a definite value, and great opposition to frequencies below this value. By combining the series
inductance and bypass capacitance, as shown in view (C), the simplest type of low-pass filter is obtained. At
point P, a much higher opposition is offered to the low frequencies by the capacitor than by the inductor, and
most of the low-frequency current takes the path of least opposition. On the other hand,
1-35
the least amount of opposition is offered to the high frequencies by the capacitor, and most of the
high- frequency energy returns to the source through the capacitor. High-PASS FILTER
a high-pass filter circuit passes all currents having a frequency higher than a specified frequency, while
opposing all currents having a frequency lower than its specified frequency. This is illustrated in figure 1-17. a
capacitor that is used in series with the source of both high and low frequencies, as shown in view (A) of figure
1-18, will respond differently to high-frequency, low-frequency, and direct currents. It will offer little
opposition to the passage of high-frequency currents, great opposition to the passage of low-frequency currents,
and completely block direct currents. The value of the capacitor must be chosen so that it allows the passage of
all currents having frequencies above the desired value, and opposes those having frequencies below the desired
value. Then, in order to shunt the undesired low-frequency currents back to the source, an inductor is used, as
shown in view (B). This inductor must have a value that will allow it to pass currents having frequencies below
the frequency cutoff point, and reject currents having frequencies above the frequency cutoff point, thus forcing
them to pass through the capacitor. By combining inductance and capacitance, as shown in view (C), you obtain the
simplest type of high-pass filter. At point P most of the high-frequency energy is passed on to the load by the
capacitor, and most of the low-frequency energy is shunted back to the source through the inductor.
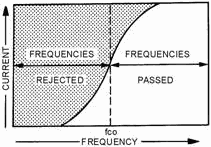
Figure 1-17. - High-pass filter response curve.
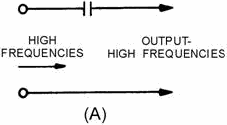
Figure 1-18A. - Components of a simple high-pass filter.
1-36
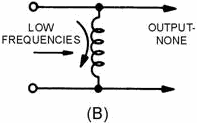
Figure 1-18B. - Components of a simple high-pass filter.
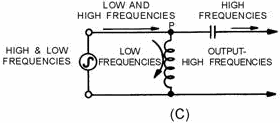
Figure 1-18C. - Components of a simple high-pass filter. RESONANT Circuits AS FILTERS Resonant circuits can be made to serve as
filters in a manner similar to the action of individual capacitors and inductors. As you know, the series-LC
circuit offers minimum opposition to currents that have frequencies at or near the resonant frequency, and maximum
opposition to currents of all other frequencies. You also know that a parallel-LC circuit offers a very
high impedance to currents that have frequencies at or near the resonant frequency, and a relatively low impedance
to currents of all other frequencies. If you use these two basic concepts, the Bandpass and Band-REJECT
filters can be constructed. The bandpass filter and the band-reject filter are two common types of filters that use resonant circuits. Bandpass Filter A bandpass filter passes a narrow band of
frequencies through a circuit and attenuates all other frequencies that are higher or lower than the desired band
of frequencies. This is shown in figure 1-19 where the greatest current exists at the center frequency (fr).
Frequencies below resonance (f1) and frequencies above resonance (f2) drop off rapidly and
are rejected.
1-37
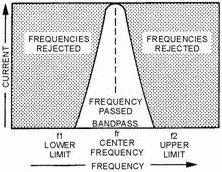
Figure 1-19. - Bandpass filter response curve. In the circuit of figure 1-20, view (A), the series-LC circuit replaces the inductor of figure 1-16,
view (A), and acts as a Bandpass filter. It passes currents having frequencies at or near its resonant frequency,
and opposes the passage of all currents having frequencies outside this band.
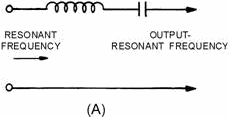
Figure 1-20A. - Components of a simple bandpass filter. Thus, in the circuit of figure 1-20, view (B), the parallel-LC circuit replaces the capacitor of figure
1- 16, view (B). If this circuit is tuned to the same frequency as the series-LC circuit, it will provide a path
for all currents having frequencies outside the limits of the frequency band passed by the series-resonant
circuit. The simplest type of bandpass filter is formed by connecting the two LC circuits as shown in figure 1-20,
view (C). The upper and lower frequency limits of the filter action are filter cutoff points.
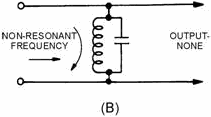
Figure 1-20B. - Components of a simple bandpass filter. 1-38
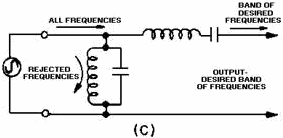
Figure 1-20C. - Components of a simple bandpass filter. Band-Reject Filter A band-reject filter circuit is used to block the passage of
current for a narrow band of frequencies, while allowing current to flow at all frequencies above or below this
band. This type of filter is also known as a Band-SUPPRESSION or Band-STOP filter. The way it responds is shown by
the response curve of figure 1-21. Since the purpose of the band-reject filter is directly opposite to that of a
bandpass filter, the relative positions of the resonant circuits in the filter are interchanged. The parallel-LC
circuit shown in figure 1-22, view (A), replaces the capacitor of figure 1-18, view (A). It acts as a band-reject
filter, blocking the passage of currents having frequencies at or near resonant frequency and passing all currents
having frequencies outside this band. The series-LC circuit shown in figure 1-22, view (B), replaces the inductor
of figure 1-18, view (B). If this series circuit is tuned, to the same frequency as the parallel circuit, it acts
as a bypass for the band of rejected frequencies. Then, the simplest type of band- reject filter is obtained by
connecting the two circuits as shown in figure 1-22, view (C).
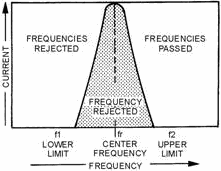
Figure 1-21. - Band-reject filter response curve. 1-39
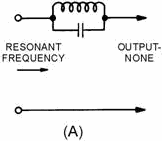
Figure 1-22A. - Components of a simple band-reject filter.
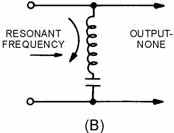
Figure 1-22B. - Components of a simple band-reject filter.
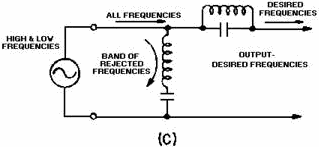
Figure 1-22C. - Components of a simple band-reject filter. Q-14. What is the device called that will separate alternating current from direct current, or that
will separate alternating current of one frequency from other alternating currents of different frequencies?
Q-15. What are the four general types of filters?
1-40
|