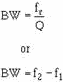Navy Electricity and Electronics Training Series (NEETS)
Module 9 - Introduction to Wave- Generation and Wave-Shaping
Chapter 1:  Pages 1-21 through 1-30

frequency selection to be accomplished in a different manner. It gives the circuit different characteristics. The first of these characteristics is the ability to store energy.
 
The Characteristics of a Typical Parallel-Resonant Circuit
 
Look at figure 1-11. In this circuit, as in other parallel circuits, the voltage is the same across the inductor and capacitor. The currents through the components vary inversely with their reactances in accordance with Ohm's law. The total current drawn by the circuit is the vector sum of the two individual component currents. Finally, these two currents, IL  and IC, are 180 degrees out of phase because the effects of L and C are opposite. There is not a single fact new to you in the above. It is all based on what you have learned previously about parallel AC circuits that contain L and C.
 

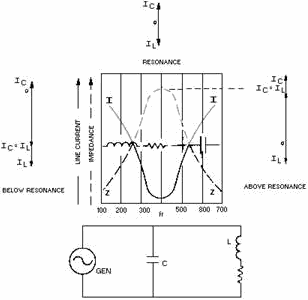
Figure 1-11. - Curves of impedance and current in an RLC parallel-resonant circuit.

 
Now, at resonance, X_L is still equal to X_C. Therefore, I_L  must equal I_C. Remember, the voltage is the same; the reactances are equal; therefore, according to Ohm's law, the currents must be equal. But, don't forget, even though the currents are equal, they are still opposites. That is, if the current is flowing "up" in the capacitor, it is flowing "down" in the coil, and vice versa. In effect, while the one component draws current, the other returns it to the source. The net effect of this "give and take action" is that zero current is drawn from the source at resonance. The two currents yield a total current of zero amperes because they are exactly equal and opposite at resonance.
 
A circuit that is completed and has a voltage applied, but has zero current, must have an INFINITE IMPEDANCE (apply Ohm's law - any voltage divided by zero yields infinity).
 
 

1-21

By now you know that we have just ignored our old friend resistance from previous discussions. In an actual circuit, at resonance, the currents will not quite counteract each other because each component will have different resistance. This resistance is kept extremely low, but it is still there. The result is that a relatively small current flows from the source at resonance instead of zero current. Therefore, a basic characteristic of a practical parallel-LC circuit is that, at resonance, the circuit has MAXIMUM impedance which results in MINIMUM current from the source. This current is often called line current. This is shown by the peak of the waveform for impedance and the valley for the line current, both
occurring at f_r  the frequency of resonance in figure 1-11.
 
There is little difference between the circuit pulsed by the battery in figure 1-8 that oscillated at its resonant (or natural) frequency, and the circuit we have just discussed. The equal and opposite currents in the two components are the same as the currents that charged and discharged the capacitor through the coil.
 
For a given source voltage, the current oscillating between the reactive parts will be stronger at the resonant frequency of the circuit than at any other frequency. At frequencies below resonance, capacitive current will decrease; above the resonant frequency, inductive current will decrease. Therefore, the oscillating current (or circulating current, as it is sometimes called), being the lesser of the two reactive currents, will be maximum at resonance.
 
If you remember, the basic resonant circuit produced a "damped" wave. A steady amplitude wave was produced by giving the circuit energy that would keep it going. To do this, the energy had to be at the same frequency as the resonant frequency of the circuit.
 
So, if the resonant frequency is "timed" right, then all other frequencies are "out of time" and produce waves that tend to buck each other. Such frequencies cannot produce strong oscillating currents.
 
In our typical parallel-resonant (LC) circuit, the line current is minimum (because the impedance is maximum). At the same time, the internal oscillating current in the tank is maximum. Oscillating current may be several hundred times as great as line current at resonance.
 
In any case, this circuit reacts differently to the resonant frequency than it does to all other frequencies. This makes it an effective frequency selector.
 
Summary of Resonance
 
Both series- and parallel-LC circuits discriminate between the resonant frequency and all other frequencies by balancing an inductive reactance against an equal capacitive reactance.
 
In series, these reactances create a very low impedance. In parallel, they create a very high impedance. These characteristics govern how and where designers use resonant circuits. A low- impedance requirement would require a series-resonant circuit. A high-impedance requirement would require the designer to use a parallel-resonant circuit.
 
Tuning a Band of Frequencies
 
Our resonant circuits so far have been tuned to a single frequency - the resonant frequency. This is fine if only one frequency is required. However, there are hundreds of stations on many different frequencies.
 
Therefore, if we go back to our original application, that of tuning to different radio stations, our resonant circuits are not practical. The reason is because a tuner for each frequency would be required and this is not practical.
 
 

1-22

What is a practical solution to this problem? The answer is simple. Make either the capacitor or the inductor variable. Remember, changing either L or C changes the resonant frequency.
 
Now you know what has been happening all of these years when you "pushed" the button or "turned" the dial. You have been changing the L or C in the tuned circuits by the amount necessary to adjust the tuner to resonate at the desired frequency. No matter how complex a unit, if it has LC tuners, the tuners obey these basic laws.
 
Q-9.   What is the term for the number of times per second that tank circuit energy is either stored in the inductor or capacitor?
 
Q-10.   In a parallel-resonant circuit, what is the relationship between impedance and current? Q-11.   When is line current minimum in a parallel-LC circuit?
 

RESONANT CIRCUITS AS FILTER CIRCUITS

 
 The principle of series- or parallel-resonant circuits have many applications in radio, television, communications, and the various other electronic fields throughout the Navy. As you have seen, by making the capacitance or inductance variable, the frequency at which a circuit will resonate can be controlled.
 
In addition to station selecting or tuning, resonant circuits can separate currents of certain frequencies from those of other frequencies.
 
Circuits in which resonant circuits are used to do this are called FILTER CIRCUITS.
 
If we can select the proper values of resistors, inductors, or capacitors, a FILTER NETWORK, or "frequency selector," can be produced which offers little opposition to one frequency, while BLOCKING or ATTENUATING other frequencies. A filter network can also be designed that will "pass" a band of frequencies and "reject" all other frequencies.
 
Most electronic circuits require the use of filters in one form or another. You have already studied several in modules 6, 7, and 8 of the NEETS.
 
One example of a filter being applied is in a rectifier circuit. As you know, an alternating voltage is changed by the rectifier to a direct current. However, the DC voltage is not pure; it is still pulsating and fluctuating. In other words, the signal still has an AC component in addition to the DC voltage. By feeding the signal through simple filter networks, the AC component is reduced. The remaining DC is as pure as the designers require.
 
Bypass capacitors, which you have already studied, are part of filter networks that, in effect, bypass, or shunt, unwanted AC components to ground.
 
THE IDEA OF "Q"
 
Several times in this chapter, we have discussed "ideal" or theoretically perfect circuits. In each case, you found that resistance kept our circuits from being perfect. You also found that low resistance in tuners was better than high resistance. Now you will learn about a factor that, in effect, measures just how close to perfect a tuner or tuner component can be. This same factor affects BANDWIDTH and SELECTIVITY. It can be used in figuring voltage across a coil or capacitor in a series-resonant circuit and the amount of circulating (tank) current in a parallel-resonant circuit. This factor is very important
 
 

1-23

and useful to designers. Technicians should have some knowledge of the factor because it affects so many things. The factor is known as Q. Some say it stands for quality (or merit). The higher the Q, the better the circuit; the lower the losses (I²R), the closer the circuit is to being perfect.
 
Having studied the first part of this chapter, you should not be surprised to learn that resistance (R) has a great effect on this figure of merit or quality.
 
Q Is a Ratio
 
Q is really very simple to understand if you think back to the tuned-circuit principles just covered. Inductance and capacitance are in all tuners. Resistance is an impurity that causes losses. Therefore, components that provide the reactance with a minimum of resistance are "purer" (more perfect) than those with higher resistance. The actual measure of this purity, merit, or quality must include the two basic quantities, X and R.
 
The ratio
 

 
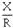
does the job for us. Let's take a look at it and see just why it measures quality.
 
First, if a perfect circuit has zero resistance, then our ratio should give a very high value of Q to reflect the high quality of the circuit. Does it?
 
Assume any value for X and a zero value for R.
 
Then:
 

 
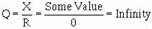
Remember, any value divided by zero equals infinity. Thus, our ratio is infinitely high for a theoretically perfect circuit.
 
With components of higher resistance, the Q is reduced. Dividing by a larger number always yields a smaller quantity. Thus, lower quality components produce a lower Q. Q, then, is a direct and accurate measure of the quality of an LC circuit.
 
Q is just a ratio. It is always just a number - no units. The higher the number, the "better" the circuit. Later as you get into more practical circuits, you may find that low Q may be desirable to provide certain characteristics. For now, consider that higher is better.
 
Because capacitors have much, much less resistance in them than inductors, the Q of a circuit is very often expressed as the Q of the coil or:
 

 
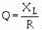
The answer you get from using this formula is very near correct for most purposes. Basically, the Q of a capacitor is so high that it does not limit the Q of the circuit in any practical way. For that reason, the technician may ignore it.
 
 

1-24

The Q of a Coil
 
Q is a feature that is designed into a coil. When the coil is used within the frequency range for which it is designed, Q is relatively constant. In this sense, it is a physical characteristic.
 
Inductance is a result of the physical makeup of a coil - number of turns, core, type of winding, etc. Inductance governs reactance at a given frequency. Resistance is inherent in the length, size, and material of the wire. Therefore, the Q of a coil is mostly dependent on physical characteristics.
 
Values of Q that are in the hundreds are very practical and often found in typical equipment.
 
Application of Q
 
For the most part, Q is the concern of designers, not technicians. Therefore, the chances of you having to figure the Q of a coil are remote. However, it is important for you to know some circuit relationships that are affected by Q.
 
Q Relationships in Series Circuits
 
Q can be used to determine the "gain" of series-resonant circuits. Gain refers to the fact that at resonance, the voltage drop across the reactances are greater than the applied voltage. Remember, when we applied Ohm's law in a series-resonant circuit, it gave us the following characteristics:
 
·    Low impedance, high current.
 
·    High current; high voltage across the comparatively high reactances.
 
This high voltage is usable where little power is required, such as in driving the grid of a vacuum tube or the gate of a field effect transistor (F.E.T.). The gain of a properly designed series-resonant circuit may be as great or greater than the amplification within the amplifier itself. The gain is a function of Q, as shown in the following example:
 

E = the input voltage to the tuned circuit
 
E_L = the voltage drop across the coil at resonance Q.
 
Q = the Q of the coil.
 
Then:
 
         E_L = EQ

If the Q of the coil were 100, then the gain would be 100; that is, the voltage of the coil would be 100 times that of the input voltage to the series circuit.
 
Resistance affects the resonance curve of a series circuit in two ways - the lower the resistance, the higher the current; also, the lower the resistance, the sharper the curve. Because low resistance causes high Q, these two facts are usually expressed as functions of Q. That is, the higher the Q, the higher and sharper the curve and the more selective the circuit.
 
The lower the Q (because of higher resistance), the lower the current curve; therefore, the broader the curve, the less selective the circuit. A summary of the major characteristics of series RLC-circuits at resonance is given in table 1-1.
 
 

1-25

Table 1-1. - Major Characteristics of Series RLC Circuits at Resonance

 
Q Relationships in a Parallel-Resonant Circuit
 
There is no voltage gain in a parallel-resonant circuit because voltage is the same across all parts of a parallel circuit. However, Q helps give us a measure of the current that circulates in the tank.
 
 

1-26

Given:
 

I_LINE = current drawn from the source
 
I_L = current through the coil (or circulating current
 
Q = the Q of the coil
 
Then:
 
     I_L = I_LINE Q

 
Again, if the Q were 100, the circulating current would be 100 times the value of the line current. This may help explain why some of the wire sizes are very large in high-power amplifying circuits.
 
The impedance curve of a parallel-resonant circuit is also affected by the Q of the circuit in a manner similar to the current curve of a series circuit. The Q of the circuit determines how much the impedance is increased across the parallel-LC circuit. (Z = Q x X_L)
 
The higher the Q, the greater the impedance at resonance and the sharper the curve. The lower the Q, the lower impedance at resonance; therefore, the broader the curve, the less selective the circuit. The major characteristics of parallel-RLC circuits at resonance are given in table 1-2.
 
 

1-27

 Table 1-2. - Major Characteristics of Parallel RLC Circuits at Resonance

 
Summary of Q
 
The ratio that is called Q is a measure of the quality of resonant circuits and circuit components. Basically, the value of Q is an inverse function of electrical power dissipated through circuit resistance. Q is the ratio of the power stored in the reactive components to the power dissipated in the resistance. That is, high power loss is low Q; low power loss is high Q.
 
Circuit designers provide the proper Q. As a technician, you should know what can change Q and what quantities in a circuit are affected by such a change.
 
 

1-28

BANDWIDTH

 
If circuit Q is low, the gain of the circuit at resonance is relatively small. The circuit does not discriminate sharply (reject the unwanted frequencies) between the resonant frequency and the frequencies on either side of resonance, as shown by the curve in figure 1-12, view (A). The range of frequencies included between the two frequencies (426.4 kHz and 483.6 kHz in this example) at which the current drops to 70 percent of its maximum value at resonance is called the BANDWIDTH of the circuit.
 

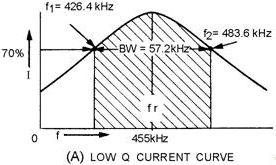
Figure 1-12A. - Bandwidth for high- and low-Q series circuit. LOW Q CURRENT CURVE.

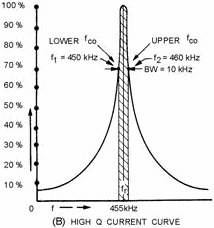
Figure 1-12B. - Bandwidth for high- and low-Q series circuit. HIGH Q CURRENT CURVE.

 
It is often necessary to state the band of frequencies that a circuit will pass. The following standard has been set up: the limiting frequencies are those at either side of resonance at which the curve falls to a point of .707 (approximately 70 percent) of the maximum value. This point is called the HALF-POWER point. Note that in figure 1-12, the series-resonant circuit has two half-power points, one above and one
 
 

1-29

below the resonant frequency point. The two points are designated upper frequency cutoff (fco) and lower frequency cutoff (f_co) or simply f₁  and f₂. The range of frequencies between these two points comprises the bandwidth. Views (A) and (B) of figure 1-12 illustrate the bandwidths for low- and high-Q resonant circuits. The bandwidth may be determined by use of the following formulas:
 

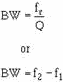
Where:
 
BW = bandwidth of a circuit in units of frequency
 
f_r = resonant frequency
 
f₂ = the upper cutoff frequency
 
f₁ = the lower cutoff frequency

 
For example, by applying the formula we can determine the bandwidth for the curve shown in figure 1-12, view (A).
 

Solution:
 
    BW= f₂ - f₁
 
    BW = 483.6 kHz - 426.4 kHz
 
    BW = 57.2 kHz

 
If the Q of the circuit represented by the curve in figure 1-12, view (B), is 45.5, what would be the bandwidth?

Solution:

 
If Q equals 7.95 for the low-Q circuit as in view (A) of figure 1-12, we can check our original calculation of the bandwidth.
 
 

1-30

NEETS Table of Contents

• Introduction to Matter, Energy, and Direct Current
• Introduction to Alternating Current and Transformers
• Introduction to Circuit Protection, Control, and Measurement
• Introduction to Electrical Conductors, Wiring Techniques, and Schematic Reading
• Introduction to Generators and Motors
• Introduction to Electronic Emission, Tubes, and Power Supplies
• Introduction to Solid-State Devices and Power Supplies
• Introduction to Amplifiers
• Introduction to Wave-Generation and Wave-Shaping Circuits
• Introduction to Wave Propagation, Transmission Lines, and Antennas
• Microwave Principles
• Modulation Principles
• Introduction to Number Systems and Logic Circuits
• Introduction to Microelectronics
• Principles of Synchros, Servos, and Gyros
• Introduction to Test Equipment
• Radio-Frequency Communications Principles
• Radar Principles
• The Technician's Handbook, Master Glossary
• Test Methods and Practices
• Introduction to Digital Computers
• Magnetic Recording
• Introduction to Fiber Optics