Module 9 - Introduction to Wave-Generation and Wave-Shaping
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
NEETS Module 9 − Introduction to Wave− Generation and Wave−Shaping Pages i, 1−1, 1−11, 1−21, 1−31, 1−41, 2−1, 2−11, 2−21, 2−31, 3−1, 3−11, 3−21, 3−31, 3−41, 3−51, 4−1, 4−11, 4−21, 4−31, 4−41, 4−51, Index
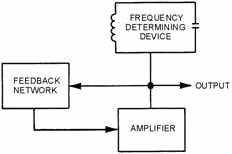
Chapter 1 Oscillators Learning Objectives Upon completion of this chapter you will be able to: 1. List the two broad classifications of oscillators (wave generators). 2. Identify the three frequency-determining devices for sine-wave oscillators. 3. Describe the differences between series-fed and shunt-fed oscillators. 4. Explain how the crystal is equivalent to the series and parallel LC circuit. 5. Identify the Armstrong oscillator. 6. Identify the Hartley oscillator. 7. Identify the Colpitts oscillator. 8. Identify the resistive-capacitive oscillator. 9. Determine the frequency of a resistive-capacitive oscillator. 10. Explain the operation of a pulsed oscillator. 11. Determine how many cycles are present in the output of a pulsed oscillator. 12. Explain how frequency multiplication takes place. Introduction WAVE GENERATORS play a prominent role in the field of electronics. They generate signals from a few hertz to several gigahertz (109 hertz). Modern wave generators use many different circuits and generate such outputs as SINUSOIDAL, SQUARE, RECTANGULAR, SAWTOOTH, and TRAPEZOIDAL waveshapes. These waveshapes serve many useful purposes in the electronic circuits you will be studying. For example, they are used extensively throughout the television receiver to reproduce both picture and sound. One type of wave generator is known as an Oscillator. An oscillator can be regarded as an amplifier which provides its own input signal. Oscillators are classified according to the waveshapes they produce and the requirements needed for them to produce oscillations. Classification of Oscillators (GENERATORS) Wave generators can be classified into two broad categories according to their output waveshapes, SINUSOIDAL and NONSINUSOIDAL. 2-1 Sinusoidal Oscillators A sinusoidal oscillator produces a sine-wave output signal. Ideally, the output signal is of constant amplitude with no variation in frequency. Actually, something less than this is usually obtained. The degree to which the ideal is approached depends upon such factors as class of amplifier operation, amplifier characteristics, frequency stability, and amplitude stability. Sine-wave generators produce signals ranging from low audio frequencies to ultrahigh radio and microwave frequencies. Many low-frequency generators use resistors and capacitors to form their frequency-determining networks and are referred to as RC Oscillators. They are widely used in the audio-frequency range. Another type of sine-wave generator uses inductors and capacitors for its frequency-determining network. This type is known as the LC Oscillator. LC oscillators, which use tank circuits, are commonly used for the higher radio frequencies. They are not suitable for use as extremely low-frequency oscillators because the inductors and capacitors would be large in size, heavy, and costly to manufacture. a third type of sine-wave generator is the Crystal-Controlled Oscillator. The crystal- controlled oscillator provides excellent frequency stability and is used from the middle of the audio range through the radio frequency range. Nonsinusoidal Oscillators Nonsinusoidal oscillators generate complex waveforms, such as square, rectangular, trigger, sawtooth, or trapezoidal. Because their outputs are generally characterized by a sudden change, or relaxation, they are often referred to as RELAXATION Oscillators. The signal frequency of these oscillators is usually governed by the charge or discharge time of a capacitor in series with a resistor. Some types, however, contain inductors that affect the output frequency. Thus, like sinusoidal oscillators, both RC and LC networks are used for determining the frequency of oscillation. Within this category of nonsinusoidal oscillators are MULTIVIBRATORS, BlockING Oscillators, SAWTOOTH GENERATORS, and TRAPEZOIDAL GENERATORS. The Basic Oscillator An oscillator can be thought of as an amplifier that provides itself (through feedback) with an input signal. By definition, it is a nonrotating device for producing alternating current, the output frequency of which is determined by the characteristics of the device. The primary purpose of an oscillator is to generate a given waveform at a constant peak amplitude and specific frequency and to maintain this waveform within certain limits of amplitude and frequency. An oscillator must provide amplification. Amplification of signal power occurs from input to output. In an oscillator, a portion of the output is fed back to sustain the input, as shown in figure 2-1. Enough power must be fed back to the input circuit for the oscillator to drive itself as does a signal generator. To cause the oscillator to be self-driven, the feedback signal must also be
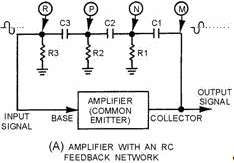
Figure 2-1. - Basic oscillator block diagram. 2-2 Regenerative (positive). Regenerative signals must have enough power to compensate for circuit losses and to maintain oscillations. Since a practical oscillator must oscillate at a predetermined frequency, a Frequency- Determining DEVICE (FDD), sometimes referred to as a Frequency-Determining Network (FDN), is needed. This device acts as a filter, allowing only the desired frequency to pass. Without a frequency-determining device, the stage will oscillate in a random manner, and a constant frequency will not be maintained. Before discussing oscillators further, let's review the requirements for an oscillator. First, amplification is required to provide the necessary gain for the signal. Second, sufficient regenerative feedback is required to sustain oscillations. Third, a frequency-determining device is needed to maintain the desired output frequency. The basic oscillator requirements, in addition to the application, determine the type of oscillator to be used. Let's consider some factors that account for the complexity and unique characteristics of oscillators. Virtually every piece of equipment that uses an oscillator has two stability requirements, Amplitude STABILITY and Frequency STABILITY. Amplitude stability refers to the ability of the oscillator to maintain a constant amplitude in the output waveform. The more constant the amplitude of the output waveform, the better the amplitude stability. Frequency stability refers to the ability of the oscillator to maintain its operating frequency. The less the oscillator varies from its operating frequency, the better the frequency stability. A constant frequency and amplitude can be achieved by taking extreme care to prevent variations in Load, BIAS, and COMPONENT Characteristics. Load variations can greatly affect the amplitude and frequency stability of the output of an oscillator. Therefore, maintaining the load as constant as possible is necessary to ensure a stable output. As you should know from your study of transistor biasing, bias variations affect the operating point of the transistor. These variations may alter the amplification capabilities of the oscillator circuits as well. a well-regulated power supply and a bias-stabilizing circuit are required to ensure a constant, uniform signal output. As a result of changing temperature and humidity conditions, the value or characteristics of components such as capacitors, resistors, and transistors can change. The changes in these components also cause changes in amplitude and frequency. Output power is another consideration in the use of oscillators. Generally speaking, high power is obtained at some sacrifice to stability. When both requirements are to be met, a low-power, stable oscillator can be followed by a higher-power BUFFER Amplifier. The buffer provides isolation between the oscillator and the load to prevent changes in the load from affecting the oscillator. If the oscillator stage must develop high power, efficiency becomes important. Many oscillators use class C bias to increase efficiency. Other types of oscillators may use class a bias when a high efficiency is not required but distortion must be kept at a minimum. Other classes of bias may also be used with certain oscillators. SINE-WAVE Oscillator RC networks, LC tanks, and crystals may appear in sine-wave oscillator circuits. An amplifier can be made into a sine-wave oscillator by providing regenerative feedback through an RC network. 2-3 RC Network Figure 2-2, view (A), shows the block diagram of an amplifier with an RC network through which regenerative feedback is provided. The RC network also acts as the frequency-determining device. View (B) shows a vector analysis of the signal E at various points in the circuit.
Figure 2-2A. - RC oscillator. Amplifier WITH and RC Feedback Network.
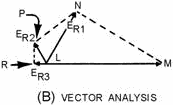
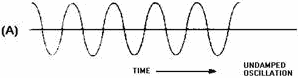
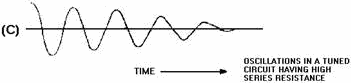
Figure 2-2B. - RC oscillator. VECTOR ANALYSIs To analyze the operation of the circuit in view (A), assume that the amplifier is a common-emitter configuration. The signal on the collector (M) is 180 degrees out of phase with the signal (input) on the base (R). For the circuit to produce regenerative feedback, the RC network must provide a 180-degree phase shift of the collector signal. When power is applied to the circuit, a noise voltage (noise contains many different frequencies) will appear on the collector. This noise signal is represented by vector LM in view (B). As the signal couples through C1 and across R1 (view (A)), a phase shift occurs. The voltage across R1 (ER1), represented by vector LN, has been shifted in phase (about 60 degrees) and reduced in amplitude. The signal at point N (view (A)) is then coupled to the next RC section (R2 and C2). Using the same size resistor and capacitor as before will cause another 60-degree phase shift to take place. The signal at point P is the voltage across R2, represented by vector LP. Now the signal at point P has been shifted about 120 degrees and its amplitude is reduced still further. The same actions occur for the last section (R3 and C3). This signal experiences another 60-degree phase shift and has further amplitude reduction. The signal at point R (ER3) has been shifted 180 degrees and is represented by vector LR. Notice that point R is the input to the base of the common-emitter amplifier. Also, vector LR shows that the signal on the base is regenerative (aiding the circuit operation). This meets the regenerative feedback requirement. An exact 60-degree phase shift per stage is not required, but the sum of the three phase shifts must equal 180 degrees. 2-4 For a given RC network, only one frequency of the initial noise signal will be shifted exactly 180 degrees. In other words, the network is frequency selective. Therefore, the RC network is the frequency- determining device since the lengths of the vectors and their phase relationships depend on frequency. The frequency of oscillations is governed by the values of resistance and capacitance in these sections. Variable resistors and capacitors may be used to provide tuning in the feedback network to allow for minor variations in phase shift. For an RC phase-shift oscillator, the amplifier is biased for class a operation to minimize distortion of the wave or signal. LC Network Some sine-wave oscillators use resonant circuits consisting of inductance and capacitance. For example, recall the tank circuit in which a resonant circuit stores energy alternately in the inductor and capacitor, producing a sine wave. You studied this action of the tank circuit in chapter 1. If there were absolutely no internal resistances in a tank circuit, oscillations would continue indefinitely, as shown in figure 2-3, view (A). Each resonant circuit does, however, contain some resistance which dissipates power. This power loss causes the amplitude to decrease, as shown in views (B) and (C). The reduction of amplitude in an oscillator circuit is referred to as DAMPING. Damping is caused by both tank and load resistances. The larger the tank resistance, the greater the amount of damping. Loading the tank causes the same effect as increasing the internal resistance of the tank. The effect of this damping can be overcome by applying regenerative feedback.
Figure 2-3A. - Effects of damping.
Figure 2-3B. - Effects of damping.
Figure 2-3C. - Effects of damping. 2-5 Figure 2-4 shows a block diagram of a typical LC oscillator. Notice that the oscillator contains the three basic requirements for sustained oscillations: amplification, a frequency-determining device, and regenerative feedback.
Figure 2-4. - LC oscillator. The amplifier supplies energy to begin what is known as the FLYWHEEL EFFECT. The flywheel effect is the maintenance of oscillations in a circuit in the intervals between pulses of excitation energy. Recall that in chapter 1 the tank circuit alternately stored energy in the inductor and capacitor. The LC network provides initial oscillations. a portion of the output of the LC network is then returned to the input of the amplifier through the regenerative-feedback network to sustain the oscillations. When a tank circuit is used to develop oscillations in an oscillator, the output frequency of the oscillator is primarily the resonant frequency of the tank circuit and can be found by the formula:
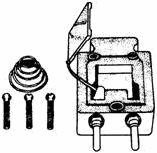
Crystals Another frequency-determining device is the Crystal. The crystal may be used with a tank circuit, or it may perform alone. Crystals exhibit a characteristic known as the PIEZOELECTRIC EFFECT. The piezoelectric effect is the property of a crystal by which mechanical forces produce electrical charges and, conversely, electrical charges produce mechanical forces. This effect is a form of oscillation similar to the flywheel effect of a tank circuit. The piezoelectric effect can be seen in a number of crystal substances. The most important of these are the minerals quartz and Rochelle salt. Although quartz does not exhibit the piezoelectric effect to the degree that Rochelle salt does, quartz is used for frequency control in oscillators because of its greater mechanical strength. Another mineral, tourmaline, is physically strong like quartz; but because it is more expensive, it is not used extensively as an FDD. This discussion will deal only with the quartz crystal. The crystals used in oscillator circuits are thin sheets, or wafers, cut from natural or synthetic quartz and ground to a specific thickness to obtain the desired resonant frequency. The crystals are mounted in holders, which support them physically and provide electrodes by which voltage is applied. The holder must allow the crystals freedom for vibration. There are many different types of holders. One type is shown in figure 2-5. 2-6
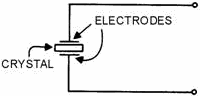
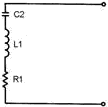
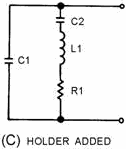
Figure 2-5. - Crystal holder. The frequency for which a crystal is ground is referred to as the NATURAL RESONANT Frequency of the crystal. Voltage applied to the crystal produces mechanical vibrations which, in turn, produce an output voltage at the natural resonant frequency of the crystal. a vibrating crystal can be represented by an equivalent electrical circuit composed of capacitance, inductance, and resistance. Figure 2-6, view (A), illustrates the symbol of a crystal; view (B) shows an equivalent circuit for the crystal. View (C) shows an equivalent circuit for the crystal and the holder; C1 represents the capacitance between the metal plates of the holder.
Figure 2-6A. - Crystal symbol and equivalent circuits. SYMBOL
Figure 2-6B. - Crystal symbol and equivalent circuits. EQUIVALENT Circuit. 2-7
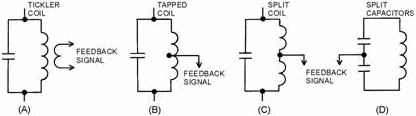
Figure 2-6C. - Crystal symbol and equivalent circuits. HOLDER ADDED The Q (discussed in chapter 1) of a crystal is many times greater than that of an LC tank circuit. The high Q is present because the resistance in the crystal is extremely small. Commercially produced crystals range in Q from 5,000 to 30,000. The high Q causes the frequency stability to be much greater than that of an ordinary LC tank circuit. This is the reason a crystal is used in many sine-wave generator circuits. Q-1. What are the two classifications of wave generators according to their output waveshapes? Q-2. What are the three networks used for frequency-determining devices? Q-3. What is another name for nonsinusoidal oscillators? Q-4. What is a nonrotating device that produces alternating current? Q-5. What are the three requirements necessary for oscillations to exist in a circuit? SOLID-STATE LC Oscillators As you have just studied, a basic oscillator can be broken down into three main sections: a frequency-determining device, an amplifier, and a feedback circuit. The frequency-determining device in an LC oscillator is usually an LC tank circuit. Although the tank circuit is normally found in the input circuit of an oscillator (both electron tube and transistor), it sometimes appears in the output circuit. The differences in magnitude of plate and collector currents and shunting impedances are considerations in the designed locations of such tank circuits. In both solid-state and electron tube circuits, oscillations take place in the tuned circuit. Both the electron tube and the transistor function primarily as electrical valves that amplify and automatically deliver to the input circuit the proper amount of energy to sustain oscillations. In both tube and transistor oscillators, the feedback circuit couples energy of the proper amount and of the correct phase from the output to the input circuit to sustain oscillations. Feedback Let's review what you have studied up to this point concerning feedback. Feedback is the process of transferring energy from a high-level point in a system to a low-level point in a system. This means transferring energy from the output of an amplifier back to its input. If the output feedback signal opposes the input signal, the signal is Degenerative or Negative Feedback. However, if the feedback aids the input signal, the feedback is Regenerative or Positive Feedback. Regenerative or 2-8 positive feedback is one of the requirements to sustain oscillations in an oscillator. This feedback can be applied in any of several ways to produce a practical oscillator circuit. TYPES of Feedback Chapter 1 described the resonant or tank circuit and how a sinusoidal signal is generated by the action of an inductor and a capacitor. The feedback signal is coupled from this circuit by either of two means. The first method is to take some of the energy from the inductor. This can be done by any one of the three ways shown in figure 2-7, views (A), (B), and (C). When an oscillator uses a TICKLER COIL, as shown in view (A), it is referred to as an ARMSTRONG Oscillator. When an oscillator uses a tapped coil (view (B)) or a split coil (view (C)), it is referred to as a HARTLEY Oscillator. The second method of coupling the feedback signal is to use two capacitors in the tank circuit and tap the feedback signal between them. This is shown in view (D). An oscillator using this method is referred to as a COLPITTS Oscillator. Each of these particular oscillators is named after the person who originally designed them.
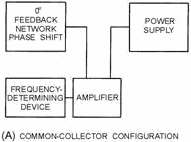
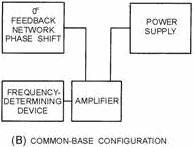
Figure 2-7. - Feedback signals. Configuration of Oscillators Any of the three basic amplifier configurations (common collector, common base, or common emitter) described in NEETS, Module 7, Introduction to Solid-State Devices and Power Supplies, Chapter 2, may be used for the oscillator circuit. However, certain considerations in the application of the circuit, such as the operating frequency and output power required, usually determine which of the three configurations is to be used. The three basic configurations are shown in figure 2-8, views (A), (B), and (C).
Figure 2-8A. - Basic configurations. Common-Collector Configuration 2-9
Figure 2-8B. - Basic configurations. Common-Base Configuration.
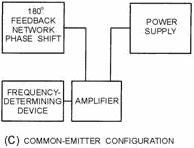
Figure 2-8C. - Basic configurations. Common-Emitter Configuration. Common-Collector Configuration Since there is no phase reversal between the input and output circuits of a common-collector configuration, the feedback network does not need to provide a phase shift. However, since the voltage gain is less than unity and the power gain is low, the common-collector configuration is very seldom used in oscillator circuits. Common-Base Configuration The power gain and voltage gain of the common-base configuration are high enough to give satisfactory operation in an oscillator circuit. The wide range between the input resistance and the output resistance make impedance matching slightly harder to achieve in the common-base circuit than in the common-emitter circuit. An advantage of the common-base configuration is that it exhibits better high- frequency response than does the common-emitter configuration. Common-Emitter Configuration The common-emitter configuration has high power gain and is used in low-frequency applications. For the energy which is fed back from the output to be in phase with the energy at the input, the feedback network of a common-emitter oscillator must provide a phase shift of approximately 180 degrees. An 2-10
|
||||||||||||||||||||||||||||||||||||||||||||||||||