Navy Electricity and Electronics Training Series (NEETS)
Module 9 - Introduction to Wave- Generation and Wave-Shaping
Chapter 1:  Pages 1-11 through 1-20

 
Now, apply Ohm's law for AC circuits:
 

 
Don't be confused by this high value of current. Our perfect, but impossible, circuit has no opposition to current. Therefore, current flow will be extremely high. The important points here are that AT RESONANCE, impedance is VERY LOW, and the resulting current will be comparatively HIGH.
 
If we apply Ohm's law to the individual reactances, we can figure relative values of voltage across each reactance.
 

E_L = I x X_L

E_C = I x X_C

 
These are reactive voltages that you have studied previously. The voltage across each reactance will be comparatively high. A comparatively high current times 2580 ohms yields a high voltage. At any given instant, this voltage will be of opposite polarity because the reactances are opposite in effect. E_L + E_C  = zero volts
 

WARNING
 
THE INDIVIDUAL VOLTAGES MAY REACH QUITE HIGH VALUES. ALTHOUGH LITTLE POWER IS PRESENT, THE VOLTAGE IS REAL AND CARE SHOULD BE TAKEN IN WORKING WITH IT.

 
Let's summarize our findings so far. In a series-LC circuit with a resonant-frequency voltage applied, the following conditions exist:
 
·   X_L and X_C  are equal and subtract to zero.
 
·   Resultant reactance is zero ohms.
 
·   Impedance (Z) is reduced to a MINIMUM value.
 
·   With minimum Z, current is MAXIMUM for a given voltage.
 
·   Maximum current causes maximum voltage drops across the individual reactances.
 
All of the above follow in sequence from the fact that X_L = X_C  at the resonant frequency.
 
 

1-11

How the Ideal Series-LC Circuit Respond to a Frequency Below Resonance (100 kHz)
 
    Given:

L = 2mH (2 x 10^-3H)
C = 300pF (300 x 10^-12F)
f_r = 205 kHz (at resonant frequency)
 
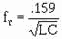
X_L = 1260 ohms (rounded off) (at 100 kHz)
X_C = 5300 ohms (rounded off) (at 100kHz)
ES = 10 volts (at 100kHz)
        (as in the previous analysis, you are given values
        that are possible for you to computer. If you do the
        computations, remember that most values are rounded off.)

 
First, note that X_L and X_C  are no longer equal. X_C  is larger than it was at resonance; X_L is smaller. By applying the formulas you have learned, you know that a lower frequency produces a higher capacitive reactance and a lower inductive reactance. The reactances subtract but do not cancel (X_L - X_C  = 1260 -5300 = 4040 ohms (capacitive)). At an input frequency of 100 kHz, the circuit (still resonant to 205 kHz)has a net reactance of 4040 ohms. In our theoretically perfect circuit, the total opposition (Z) is equal to X, or 4040 ohms.
 
As before, let's apply Ohm's law to the new conditions.
 

The voltage drops across the reactances are as follows:
 

E_L = I x X_L
E_L = .0025 A x 1260 Ω
E_L = 3 volts (approximately)
E_C = I x X_C
E_C = .0025 A x 5300 Ω
E_C = 13 volts (approximately)   

1-12

In summary, in a series-LC circuit with a source voltage that is below the resonant frequency (100 kHz in the example), the resultant reactance (X), and therefore impedance, is higher than at resonance. In addition current is lower, and the voltage drops across the reactances are lower. All of the above follow in sequence due to the fact that X_C  is greater than X_L at any frequency lower than the resonant frequency.
 
How the Ideal Series-LC Circuit Responds to a Frequency Above Resonance (300 kHz)
 
    Given:
 

L = 2mH (2 x 10^-3H)
C = 300pF (300 x 10^-12F)
f_r = 205 kHz (at resonant frequency)
X_L = 3770 ohms (rounded off) (at 300kHz)
X_C = 1770 ohms (rounded off) (at 300 kHz)
E_S = 10 volts (at 300 kHz)
 

Again, X_L and X_C  are not equal. This time, X_L is larger than X_C. (If you don't know why, apply the formulas and review the past several pages.) The resultant reactance is 2000 ohms (X_L - X_C  = 3770 - 1770 = 2000 ohms.) Therefore, the resultant reactance (X), or the impedance of our perfect circuit at 300 kHz, is 2000 ohms.
 
By applying Ohm's law as before:
 

I = 5 milliamperes
E_L = 19 volts (rounded off)
E_C = 9 volts (rounded off)

 
In summary, in a series-LC circuit with a source voltage that is above the resonant frequency (300 kHz in this example), impedance is higher than at resonance, current is lower, and the voltage drops across the reactances are lower. All of the above follow in sequence from the fact that X_L is greater than X_C  at any frequency higher than the resonant frequency.
 
Summary of the Response of the Ideal Series-LC Circuit to Frequencies Above, Below, and at Resonance
 
The ideal series-resonant circuit has zero impedance. The impedance increases for frequencies higher and lower than the resonant frequency. The impedance characteristic of the ideal series-resonant circuit results because resultant reactance is zero ohms at resonance and ONLY at resonance. All other frequencies provide a resultant reactance greater than zero.
 
Zero impedance at resonance allows maximum current. All other frequencies have a reduced current because of the increased impedance. The voltage across the reactance is greatest at resonance because voltage drop is directly proportional to current. All discrimination between frequencies results from the fact that X_L and X_C  completely counteract ONLY at the resonant frequency.
 
 

1-13

How the Typical Series-LC Circuit Differs From the Ideal
 
As you learned much earlier in this series, resistance is always present in practical electrical circuits; it is impossible to eliminate. A typical series-LC circuit, then, has R as well as L and C.
 
If our perfect (ideal) circuit has zero resistance, and a typical circuit has "some" resistance, then a circuit with a very small resistance is closer to being perfect than one that has a large resistance. Let's list what happens in a series-resonant circuit because resistance is present. This is not new to you - just a review of what you have learned previously.
 
In a series-resonant circuit that is basically L and C, but that contains "some" R, the following statements are true:
 
·   X_L, X_C, and R components are all present and can be shown on a vector diagram, each at right angles with the resistance vector (baseline).
 
·   At resonance, the resultant reactance is zero ohms. Thus, at resonance, The circuit impedance equals only the resistance (R). The circuit impedance can never be less than R because the original resistance will always be present in the circuit.
 
·   At resonance, a practical series-RLC circuit ALWAYS has MINIMUM impedance. The actual value of impedance is that of the resistance present in the circuit (Z = R).
 
Now, if the designers do their very best (and they do) to keep the value of resistance in a practical series-RLC circuit LOW, then we can still get a fairly high current at resonance. The current is NOT "infinitely" high as in our ideal circuit, but is still higher than at any other frequency. The curve and vector relationships for the practical circuit are shown in figure 1-7.
 
 

1-14

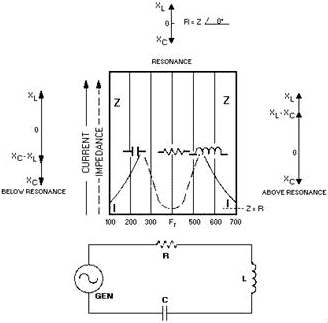
Figure 1-7. - Curves of impedance and current in an RLC series resonant circuit.

 
Note that the impedance curve does not reach zero at its minimum point. The vectors above and below resonance show that the phase shift of the circuit at these frequencies is less than 90 degrees because of the resistance.
 
The horizontal width of the curve is a measure of how well the circuit will pick out (discriminate) the one desired frequency. The width is called BANDWIDTH, and the ability to discriminate between frequencies is known as SELECTIVITY. Both of these characteristics are affected by resistance. Lower resistance allows narrower bandwidth, which is the same as saying the circuit has better selectivity. Resistance, then, is an unwanted quantity that cannot be eliminated but can be kept to a minimum by the circuit designers.
 
More on bandwidth, selectivity, and measuring the effects of resistance in resonant circuits will follow the discussion of parallel resonance.
 
Q-3.   State the formula for resonant frequency.
 
Q-4.   If the inductor and capacitor values are increased, what happens to the resonant frequency?
 
Q-5.   In an "ideal" resonant circuit, what is the relationship between impedance and current?
 
Q-6.   In a series-RLC circuit, what is the condition of the circuit if there is high impedance, low current, and low reactance voltages?
 
 

1-15

How the Parallel-LC Circuit Stores Energy
 
A parallel-LC circuit is often called a TANK CIRCUIT because it can store energy much as a tank stores liquid. It has the ability to take energy fed to it from a power source, store this energy alternately in the inductor and capacitor, and produce an output which is a continuous AC wave. You can understand how this is accomplished by carefully studying the sequence of events shown in figure 1-8. You must thoroughly understand the capacitor and inductor action in this figure before you proceed further in the study of parallel-resonant circuits.
 
In each view of figure 1-8, the waveform is of the charging and discharging CAPACITOR VOLTAGE. In view (A), the switch has been moved to position C. The DC voltage is applied across the capacitor, and the capacitor charges to the potential of the battery.
 

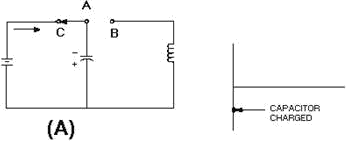
Figure 1-8A. - Capacitor and inductor action in a tank circuit.

 
In view (B), moving the switch to the right completes the circuit from the capacitor to the inductor and places the inductor in series with the capacitor. This furnishes a path for the excess electrons on the upper plate of the capacitor to flow to the lower plate, and thus starts neutralizing the capacitor charge. As these electrons flow through the coil, a magnetic field is built up around the coil. The energy which was first stored by the electrostatic field of the capacitor is now stored in the electromagnetic field of the inductor.
 

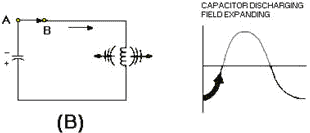
Figure 1-8B. - Capacitor and inductor action in a tank circuit.

1-16

View (C) shows the capacitor discharged and a maximum magnetic field around the coil. The energy originally stored in the capacitor is now stored entirely in the magnetic field of the coil.
 

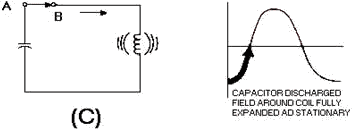
Figure 1-8C. - Capacitor and inductor action in a tank circuit.

 
Since the capacitor is now completely discharged, the magnetic field surrounding the coil starts to collapse. This induces a voltage in the coil which causes the current to continue flowing in the same direction and charges the capacitor again. This time the capacitor charges to the opposite polarity, view (D).
 

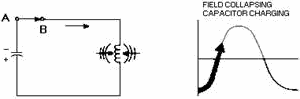
Figure 1-8D. - Capacitor and inductor action in a tank circuit.

 
In view (E), the magnetic field has completely collapsed, and the capacitor has become charged with the opposite polarity. All of the energy is again stored in the capacitor.
 
 

1-17

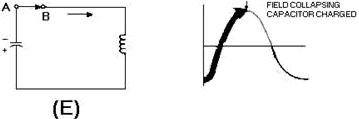
Figure 1-8E. - Capacitor and inductor action in a tank circuit.

 
 In view (F), the capacitor now discharges back through the coil. This discharge current causes the magnetic field to build up again around the coil.
 

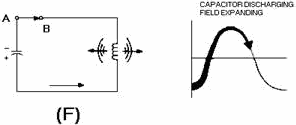
Figure 1-8F. - Capacitor and inductor action in a tank circuit.

 
In view (G), the capacitor is completely discharged. The magnetic field is again at maximum.
 

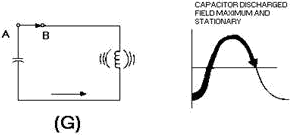
Figure 1-8G. - Capacitor and inductor action in a tank circuit.

1-18

In view (H), with the capacitor completely discharged, the magnetic field again starts collapsing. The induced voltage from the coil maintains current flowing toward the upper plate of the capacitor.
 

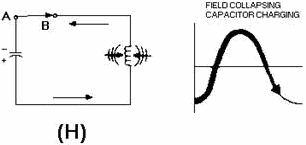
Figure 1-8H. - Capacitor and inductor action in a tank circuit.

 
In view (I), by the time the magnetic field has completely collapsed, the capacitor is again charged with the same polarity as it had in view (A). The energy is again stored in the capacitor, and the cycle is ready to start again.
 

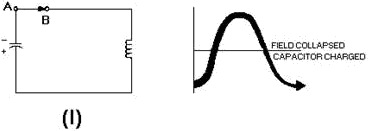
Figure 1-8I. - Capacitor and inductor action in a tank circuit.

 
The number of times per second that these events in figure 1-8 take place is called NATURAL FREQUENCY or RESONANT FREQUENCY of the circuit. Such a circuit is said to oscillate at its resonant frequency.
 
It might seem that these oscillations could go on forever. You know better, however, if you apply what you have already learned about electric circuits.
 
This circuit, as all others, has some resistance. Even the relatively small resistance of the coil and the connecting wires cause energy to be dissipated in the form of heat (I2R loss). The heat loss in the circuit resistance causes the charge on the capacitor to be less for each subsequent cycle. The result is a DAMPED WAVE, as shown in figure 1-9. The charging and discharging action will continue until all of the energy has been radiated or dissipated as heat.
 
 

1-19

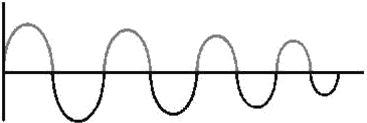
Figure 1-9. - Damped wave.

 
If it were possible to have a circuit with absolutely no resistance, there would be no heat loss, and the oscillations would tend to continue indefinitely. You have already learned that tuned circuits are designed to have very little resistance. Reducing I2R losses is still another reason for having low resistance.
 
A "perfect" tuned circuit would produce the continuous sine wave shown in figure 1-10. Its frequency would be that of the circuit.
 

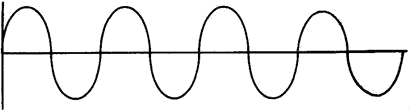
Figure 1-10. - Sine wave-resonant frequency.

 
Because we don't have perfection, another way of causing a circuit to oscillate indefinitely would be to apply a continuous AC or pulsing source to the circuit. If the source is at the resonant frequency of the circuit, the circuit will oscillate as long as the source is applied.
 
The reasons why the circuit in figure 1-8 oscillates at the resonant frequency have to do with the characteristics of resonant circuits. The discussion of parallel resonance will not be as detailed as that for series resonance because the idea of resonance is the same for both circuits. Certain characteristics differ as a result of L and C being in parallel rather than in series. These differences will be emphasized.
 
Q-7.   When the capacitor is completely discharged, where is the energy of the tank circuit stored?
 
Q-8.   When the magnetic field of the inductor is completely collapsed, where is the energy of the tank circuit stored?
 
PARALLEL RESONANCE
 
Much of what you have learned about resonance and series-LC circuits can be applied directly to parallel-LC circuits. The purpose of the two circuits is the same - to select a specific frequency and reject all others. XL still equals XC  at resonance. Because the inductor and capacitor are in parallel, however, the circuit has the basic characteristics of an AC parallel circuit. The parallel hookup causes
 
 

1-20

NEETS Table of Contents

• Introduction to Matter, Energy, and Direct Current
• Introduction to Alternating Current and Transformers
• Introduction to Circuit Protection, Control, and Measurement
• Introduction to Electrical Conductors, Wiring Techniques, and Schematic Reading
• Introduction to Generators and Motors
• Introduction to Electronic Emission, Tubes, and Power Supplies
• Introduction to Solid-State Devices and Power Supplies
• Introduction to Amplifiers
• Introduction to Wave-Generation and Wave-Shaping Circuits
• Introduction to Wave Propagation, Transmission Lines, and Antennas
• Microwave Principles
• Modulation Principles
• Introduction to Number Systems and Logic Circuits
• Introduction to Microelectronics
• Principles of Synchros, Servos, and Gyros
• Introduction to Test Equipment
• Radio-Frequency Communications Principles
• Radar Principles
• The Technician's Handbook, Master Glossary
• Test Methods and Practices
• Introduction to Digital Computers
• Magnetic Recording
• Introduction to Fiber Optics