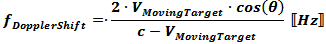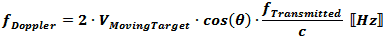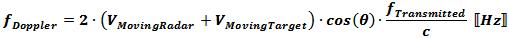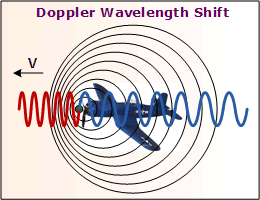
|
 Doppler shift is an apparent change in frequency
(and, correspondingly, wavelength) due to the relative motion of two objects. Per
the lower right drawing, the wavefront of the moving object is compressed and shortens
the wavelength in that region (increases frequency) and lengthens the wavelength
(decreases frequency) in the region behind it. As shown in the upper right drawing,
either one or both of the objects may be moving with respect to the ground.
Radar systems exploit the Doppler shift to provide an indication of relative
speed. When the two objects are approaching each other (closing), the Doppler shift
causes a shortening of wavelength (increase in frequency). When the two objects
are receding from each other (opening), the Doppler shift causes a lengthening of
wavelength (decrease in frequency).
For a Doppler radar system to measure speed, an accurate measurement of the original
transmitted frequency and the reflected return frequency is required. The difference
in the two frequencies is the termed the Doppler frequency shift, and is a direct
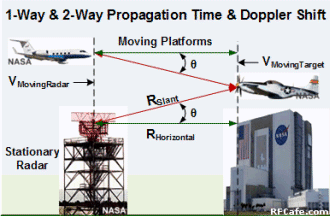
indication of the object's speed as indicated in the equations below. The measured
speed is relative to a straight line directly from the radar to the target (RHorizontal)
- not its speed relative to the ground (RSlant). To calculate
ground speed, the target's height relative to the radar antenna must be known, and
that can be inferred from the elevation angle of the antenna (known as boresight
angle, θ).
Note that the angle shown (θ) is for elevation differences only. If there
is also an azimuthal angle, it must be factored into the equation as cos (α),
where 'α' is the azimuth angle relative to the radar antenna boresight direction.
RHorizontal = RSlant
* cos θ.
In the following equations, distance can be expressed in any convenient units
as long as they are consistent for both 'V' and 'c,' that is, km/hr, mi/hr, cm/week,
furlongs/fortnight, etc. Use positive velocity (+) when the target is moving away
from the radar and negative (-) when moving toward. 'c' is the speed of light.
fTransmitted should have units of Hz since the Doppler shift
is usually no more than a few kHz.
Note: When using these formulas, be sure to keep dimensional
units consistent; i.e., do not mix kHz with MHz, mm with inches, etc. It is safer
to use base units (e.g., Hz, m) for calculation, then convert result to desired
units.
Here is information on propagation time,
radar equation, and
path loss.
Radar Doppler Frequency Shift Equation
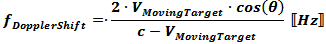
This equation applies generally to any value of VMovingTarget; however,
for VMovingTarget <<
c, VMovingTarget
- c →
c and the equation simplifies to the ones shown below.
Note: The factor of 2 in the equation is due to a Doppler
shift occurring both for the incident and reflected wave. When
calculating Doppler shift
from an emitter, such as light from a star or from a satellite, replace 2 with 1.
Example 1: An airplane moving at Mach 1 along the antenna boresight of a
10 GHz radar creates a Doppler shift of 22.87 kHz.
Example 2: The
SCR-270 radar in use at Pearl Harbor during the Japanese attack
on December 7, 1941, operated at 106 MHz and an
A6M Zero
attack aircraft had a diving speed of around 400 mi/hr. That corresponds to a Doppler
shift of a mere 633 Hz.
Fixed Radar with Moving Target
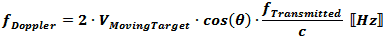
where VMovingTarget is relative to the stationary radar.
Moving Radar with Moving Target
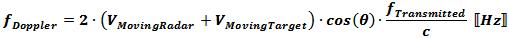
where VMovingRadar and VMovingTarget are relative to a
fixed point on the ground.
You might also want to check out the
Doppler Shift section
of the Electronic Warfare and Radar Systems Engineering Handbook.
|
