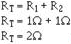Module 8 - Introduction to Amplifiers
Pages i,
1-1,
1-11,
1-21,
1-31,
2-1,
2-11,
2-21,
2-31,
3-1,
3-11,
3-21,
3-31,
3-41,
3-51,
3-61,
AI-1,
Index
| - |
Matter, Energy,
and Direct Current |
| - |
Alternating Current and Transformers |
| - |
Circuit Protection, Control, and Measurement |
| - |
Electrical Conductors, Wiring Techniques,
and Schematic Reading |
| - |
Generators and Motors |
| - |
Electronic Emission, Tubes, and Power Supplies |
| - |
Solid-State Devices and Power Supplies |
| - |
Amplifiers |
| - |
Wave-Generation and Wave-Shaping Circuits |
| - |
Wave Propagation, Transmission Lines, and
Antennas |
| - |
Microwave Principles |
| - |
Modulation Principles |
| - |
Introduction to Number Systems and Logic Circuits |
| - |
- Introduction to Microelectronics |
| - |
Principles of Synchros, Servos, and Gyros |
| - |
Introduction to Test Equipment |
| - |
Radio-Frequency Communications Principles |
| - |
Radar Principles |
| - |
The Technician's Handbook, Master Glossary |
| - |
Test Methods and Practices |
| - |
Introduction to Digital Computers |
| - |
Magnetic Recording |
| - |
Introduction to Fiber Optics |
| Note: Navy Electricity and Electronics Training
Series (NEETS) content is U.S. Navy property in the public domain. |
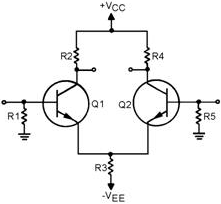
Figure 3-6. - Differential amplifier.
Even though this circuit is designed to have two inputs and two outputs, it is
not necessary to use both inputs and both outputs. (Remember, a differential amplifier
was defined as having two possible inputs and two possible outputs.) a differential
amplifier can be connected as a single-input, single-output device; a single-input,
differential-output device; or a differential-input, differential-output device.
Q-1. How many inputs and outputs are possible with a differential
amplifier?
Q-2. What two transistor amplifier configurations are combined in
the single-transistor, two-input, single-output difference amplifier?
Q-3. If the two input signals of a difference amplifier are in phase
and equal in amplitude, what will the output signal be?
Q-4. If the two input signals to a difference amplifier are equal
in amplitude and 180 degrees out of phase, what will the output signal be?
Q-5. If only one input signal is used with a difference amplifier,
what will the output signal be?
Q-6. If the two input signals to a difference amplifier are equal
in amplitude but neither in phase nor 180 degrees out of phase, what will the output
signal be?
Single-Input, Single-Output, Differential Amplifier
Figure 3-7 shows a differential amplifier with one input (the base of Q1) and
one output (the collector of Q2). The second input (the base of Q2) is grounded
and the second output (the collector of Q1) is not used.
3-11

Figure 3-7. - Single-input, single-output differential amplifier.
When the input signal developed by R1 goes positive, the current through Q1 increases.
This increased current causes a positive-going signal at the top of R3. This signal
is felt on the emitter of Q2. Since the base of Q2 is grounded, the current through
Q2 decreases with a positive-going signal on the emitter. This decreased current
causes less voltage drop across R4. Therefore, the voltage at the bottom of R4 increases
and a positive-going signal is felt at the output.
When the input signal developed by R1 goes negative, the current through Q1 decreases.
This decreased current causes a negative-going signal at the top of R3. This signal
is felt on the emitter of Q2. When the emitter of Q2 goes negative, the current
through Q2 increases. This increased current causes more of a voltage drop across
R4. Therefore, the voltage at the bottom of R4 decreases and a negative- going signal
is felt at the output.
This single-input, single-output, differential amplifier is very similar to a
single-transistor amplifier as far as input and output signals are concerned. This use of a differential amplifier does provide amplification of a.c. or d.c. signals
but does not take full advantage of the characteristics of a differential amplifier.
Single-Input, Differential-Output, Differential Amplifier
In chapter one of this module you were shown several phase splitters. You should
remember that a phase splitter provides two outputs from a single input. These two
outputs are 180 degrees out of phase with each other. The single-input, differential-output,
differential amplifier will do the same thing.
Figure 3-8 shows a differential amplifier with one input (the base of Q1) and
two outputs (the collectors of Q1 and Q2). One output is in phase with the input
signal, and the other output is 180 degrees out of phase with the input signal.
The outputs are differential outputs.
3-12

Figure 3-8. - Single-input, differential-output differential amplifier.
This circuit's operation is the same as for the single-input, single-output differential
amplifier just described. However, another output is obtained from the bottom of
R2. As the input signal goes positive, thus causing increased current through Q1,
R2 has a greater voltage drop. The output signal at the bottom of R2 therefore is
negative going. a negative-going input signal will decrease current and reverse
the polarities of both output signals.
Now you see how a differential amplifier can produce two amplified, differential
output signals from a single-input signal. One further point of interest about this
configuration is that if a combined output signal is taken between outputs number
one and two, this single output will be twice the amplitude of the individual outputs.
In other words, you can double the gain of the differential amplifier (single output)
by taking the output signal between the two output terminals. This single-output
signal will be in phase with the input signal. This is shown by the phantom signal
above R5 (the phantom resistor connected between outputs number one and two would
be used to develop this signal).
Differential-Input, Differential-Output, Differential Amplifier
When a differential amplifier is connected with a differential input and a differential
output, the full potential of the circuit is used. Figure 3-9 shows a differential
amplifier with this type of configuration (differential-input, differential-output).
3-13

Figure 3-9. - Differential-input, differential-output differential amplifier.
Normally, this configuration uses two input signals that are 180 degrees out
of phase. This causes the difference (differential) signal to be twice as large
as either input alone. (This is just like the two-input, single-output difference
amplifier with input signals that are 180 degrees out of phase.)
Output number one is a signal that is in phase with input number two, and output
number two is a signal that is in phase with input number one. The amplitude of
each output signal is the input signal multiplied by the gain of the amplifier.
With 180-degree-out-of-phase input signals, each output signal is greater in amplitude
than either input signal by a factor of the gain of the amplifier.
When an output signal is taken between the two output terminals of the amplifier
(as shown by the phantom connections, resistor, and signal), the combined output
signal is twice as great in amplitude as either signal at output number one or output
number two. (This is because output number one and output number two are 180 degrees
out of phase with each other.) When the input signals are 180 degrees out of phase,
the amplitude of the combined output signal is equal to the amplitude of one input
signal multiplied by two times the gain of the amplifier.
When the input signals are not 180 degrees out of phase, the combined output
signal taken across output one and output two is similar to the output that you
were shown for the two-input, single-output, difference amplifier. The differential
amplifier can have two outputs (180 degrees out of phase with each other), or the
outputs can be combined as shown in figure 3-9.
In answering Q7 through Q9 use the following information: All input signals are
sine waves with a peak-to-peak amplitude of 10 millivolts. The gain of the differential
amplifier is 10.
Q-7. If the differential amplifier is configured with a single input
and a single output, what will the peak-to-peak amplitude of the output signal be?
3-14
Q-8. If the differential amplifier is configured with a single input
and differential outputs, what will the output signals be?
Q-9. If the single-input, differential-output, differential amplifier
has an output signal taken between the two output terminals, what will the peak-to-peak
amplitude of this combined output be?
In answering Q10 through Q14 use the following information: a differential amplifier
is configured with a differential input and a differential output. All input signals
are sine waves with a peak-to-peak amplitude of 10 millivolts. The gain of the differential
amplifier is 10.
Q-10. If the input signals are in phase, what will be the peak-to-peak
amplitude of the output signals?
Q-11. If the input signals are 180 degrees out of phase with each
other, what will be the peak-to-peak amplitude of the output signals?
Q-12. If the input signals are 180 degrees out of phase with each
other, what will the phase relationship be between (a) the output signals and (b)
the input and output signals?
Q-13. If the input signals are 180 degrees out of phase with each
other and a combined output is taken between the two output terminals, what will
the amplitude of the combined output signal be?
Q-14. If the input signals are 90 degrees out of phase with each
other and a combined output is taken between the two output terminals, (a) what
will the peak-to-peak amplitude of the combined output signal be, and (b) will the
combined output signal be a sine wave?
Operational Amplifiers
An Operational Amplifier (OP AMP) is an amplifier which is designed to be used
with other circuit components to perform either computing functions (addition, subtraction)
or some type of transfer operation, such as filtering. Operational amplifiers are
usually high-gain amplifiers with the amount of gain determined by feedback.
Operational amplifiers have been in use for some time. They were originally developed
for analog (non-digital) computers and used to perform mathematical functions. Operational
amplifiers were not used in other devices very much because they were expensive
and more complicated than other circuits.
Today many devices use operational amplifiers. Operational amplifiers are used
as d.c. amplifiers, a.c. amplifiers, comparators, oscillators (which are covered
in NEETS, Module 9), filter circuits, and many other applications. The reason for
this widespread use of the operational amplifier is that it is a very versatile
and efficient device. As an integrated circuit (chip) the operational amplifier
has become an inexpensive and readily available "building block" for many devices.
In fact, an operational amplifier in integrated circuit form is no more expensive
than a good transistor.
Characteristics of an Operational Amplifier
The schematic symbols for an operational amplifier are shown in figure 3-10.
View (A) shows the power supply requirements while view (B) shows only the input
and output terminals. An operational amplifier is a special type of high-gain, d.c.
amplifier. To be classified as an operational amplifier, the circuit must have certain
characteristics. The three most important characteristics of an operational amplifier
are:
3-15
1. Very high gain
2. Very high input impedance
3. Very low output impedance
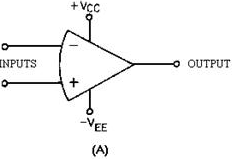
Figure 3-10A. - Schematic symbols of an operational amplifier.
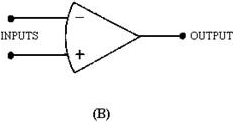
Figure 3-10B. - Schematic symbols of an operational amplifier.
Since no single amplifier stage can provide all these characteristics well enough
to be considered an operational amplifier, various amplifier stages are connected
together. The total circuit made up of these individual stages is called an operational
amplifier. This circuit (the operational amplifier) can be made up of individual
components (transistors, resistors, capacitors, etc.), but the most common form
of the operational amplifier is an integrated circuit. The integrated circuit (chip)
will contain the various stages
of the operational amplifier and can be treated and used as if it were a single
stage.
Block Diagram of an Operational Amplifier
Figure 3-11 is a block diagram of an operational amplifier. Notice that there
are three stages within the operational amplifier.
3-16

Figure 3-11. - Block diagram of an operational amplifier.
The input stage is a differential amplifier. The differential amplifier used
as an input stage provides differential inputs and a frequency response down to
d.c. Special techniques are used to provide the high input impedance necessary for
the operational amplifier.
The second stage is a high-gain voltage amplifier. This stage may be made from
several transistors to provide high gain. a typical operational amplifier could
have a voltage gain of 200,000. Most of this gain comes from the voltage amplifier
stage.
The final stage of the OP AMP is an output amplifier. The output amplifier provides
low output impedance. The actual circuit used could be an emitter follower. The
output stage should allow the operational amplifier to deliver several milliamperes
to a load.
Notice that the operational amplifier has a positive power supply (+VCC)
and a negative power supply (-V EE). This arrangement enables the operational amplifier
to produce either a positive or a negative output.
The two input terminals are labeled "inverting input" (-) and "noninverting input"
(+). The operational amplifier can be used with three different input conditions
(modes). With differential inputs (first mode), both input terminals are used and
two input signals which are 180 degrees out of phase with each other are used. This
produces an output signal that is in phase with the signal on the noninverting input.
If the noninverting input is grounded and a signal is applied to the inverting input
(second mode), the output signal will be 180 degrees out of phase with the input
signal (and one-half the amplitude of the first mode output). If the inverting input
is grounded and a signal is applied to the noninverting input (third mode), the
output signal will be in phase with the input signal (and one-half the amplitude
of the first mode output).
Q-15. What are the three requirements for an operational amplifier?
3-17
Q-16. What is the most commonly used form of the operational amplifier?
Q-17. Draw the schematic symbol for an operational amplifier.
Q-18. Label the parts of the operational amplifier shown in figure
3-12.

Figure 3-12. - Operational amplifier.
Closed-Loop Operation of an Operational Amplifier
Operational amplifiers can have either a closed-loop operation or an open-loop
operation. The operation (closed-loop or open-loop) is determined by whether or
not feedback is used. Without feedback the operational amplifier has an open-loop
operation. This open-loop operation is practical only when the operational amplifier
is used as a comparator (a circuit which compares two input signals or compares
an input signal to some fixed level of voltage). As an amplifier, the open-loop
operation is not practical because the very high gain of the operational amplifier
creates poor stability. (Noise and other unwanted signals are amplified so much
in open-loop operation that the operational amplifier is usually not used in this
way.) Therefore, most operational amplifiers are used with feedback (closed-loop
operation).
Operational amplifiers are used with degenerative (or negative) feedback which
reduces the gain of the operational amplifier but greatly increases the stability
of the circuit. In the closed-loop configuration, the output signal is applied back
to one of the input terminals. This feedback is always degenerative (negative).
In other words, the feedback signal always opposes the effects of the original input
signal. One result of degenerative feedback is that the inverting and noninverting
inputs to the operational amplifier will be kept at the same potential.
Closed-loop circuits can be of the inverting configuration or noninverting configuration.
Since the inverting configuration is used more often than the noninverting configuration,
the inverting configuration will be shown first.
Inverting Configuration
Figure 3-13 shows an operational amplifier in a closed-loop, inverting configuration.
Resistor R2 is used to feed part of the output signal back to the input of the operational
amplifier.
3-18

Figure 3-13. - Inverting configuration.
At this point it is important to keep in mind the difference between the entire
circuit (or operational circuit) and the operational amplifier. The operational
amplifier is represented by the triangle-like symbol while the operational circuit
includes the resistors and any other components as well as the operational amplifier.
In other words, the input to the circuit is shown in figure 3-13, but the signal
at the inverting input of the operational amplifier is determined by the feedback
signal as well as by the circuit input signal.
As you can see in figure 3-13, the output signal is 180 degrees out of phase
with the input signal. The feedback signal is a portion of the output signal and,
therefore, also 180 degrees out of phase with the
input signal. Whenever the input signal goes positive, the output signal and
the feedback signal go negative. The result of this is that the inverting input
to the operational amplifier is always very close to 0 volts with this configuration.
In fact, with the noninverting input grounded, the voltage at the inverting input
to the operational amplifier is so small compared to other voltages in the circuit
that it is considered to be VIRTUAL Ground. (Remember, in a closed-loop operation
the inverting and noninverting inputs are at the same potential.)
Virtual ground is a point in a circuit which is at ground potential (0 volts)
but is NOT connected to ground. Figure 3-14, (view A) (view B) and (view C), shows
an example of several circuits with points at virtual ground.

Figure 3-14A. - Virtual ground circuits.
3-19

Figure 3-14B. - Virtual ground circuits.
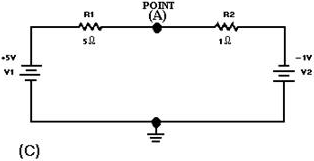
Figure 3-14C. - Virtual ground circuits.
In view (A), V1 (the left-hand battery) supplies +10 volts to the circuit while
V2 (the right-hand battery) supplies -10 volts to the circuit. The total difference
in potential in the circuit is 20 volts.
The total resistance of the circuit can be calculated:
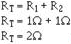
Now that the total resistance is known, the circuit current can be calculated:
3-20
|