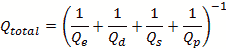Sunshine Design Engineering Services
Joe Cahak, RF engineer and owner of Sunshine Design Engineering Services, just sent me another paper
he has authored on the subject of determining the quality factor ("Q") of rectangular and cylindrical
cavities. Before you decide to skip reading this article because the topic might seem too esoteric,
Joe does much more than present formulas and tables. He also includes a tale of the research needed
to cull and vet the many, often conflicting, opinions of which formulas are correct. Ultimately, a decision
was made to select formulas that most closely matched empirically determined (measured) values from
published data. If Mr. John T. Frye was still writing
Carl & Jerry adventures for Popular Electronics,, this might make a good
story line.
See list of all of Joe's articles at bottom of page.
Searching for the Q
By Joseph L. Cahak
Copyright 2014 Sunshine Design Engineering Services
What is Q? Q, or Quality factor, is the measure of the ability of a cavity or other resonant structure
to have and hold energy. Another description is the center frequency of a resonant circuit divided by
the 3 dB Bandwidth.
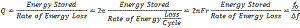
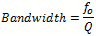
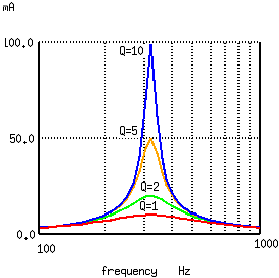
Figure 1 - Bandwidth vs Q of resonant circuit courtesy
AllAboutCircuits.com
The search for the Q began after I got an email from an engineer at a filter manufacturer. He had
purchased my RF Calculator and desired
to see if I could add the calculation for rectangular and cylindrical cavities with their Q. His company
had something they used internally and he sent me their code to look at. No documentation or details
about how to use it was included. So, it wasn't much use, other than to review and see if it matched
anything I found; it did somewhat. His calculation was one of the five for the rectangular prism case
where the mode orders l, m & n are all non zero.
With this article I would like to tell you a story of one of my recent development projects for an
addition to my RF Calculator product.
I hope you will forgive my indulgence in telling it. I am a consulting RF/Microwave Test Engineer with
process automation and application development as specialties. I design, build and program automated
test systems. I also do some application development for myself and for sale. I have been in the RF/Microwave
business for 30 years collecting reference literature all along. I have a rather large collection of
engineering books, notes, articles and digital content. The formulas cover the gamut from RF, microwave,
astronomy, physics, math, chemistry, electronics, programming and lots more. Having the formulas at
hand and easy to use and understand is key to making them useful. Lugging all the books around is not
an option, nor is trying to correctly recalling them all by memory.
Over the years I worked in BASIC, Pascal, Fortran, HP Basic, HT Basic, QBasic then Visual Basic 3
thru 6, Borland C and Microsoft C, VB.net, C# and now LabVIEW. The question with software libraries
for sale is what language makes it marketable? There are so many different programming environments
out there today that targeting a specific language or programming environment is a difficult decision.
The programming environments of choice have gone thru many changes over the years. My choice for these
calculator applications was a light weight Windows program in Visual Basic. It is easy to program and
install and the Windows executable still works on Windows 7 and 8. For more modern RF Test development
I program more with LabVIEW now and compile libraries (DLL) and as LabVIEW Libraries. I am considering
going to the mobile platform for the applications, but haven't been able to afford the development tools
yet.
About 15 years ago I started collating the best formulas in my
RF Calculator program. I also developed
a rather useful astronomy calculation product called AstroCalculator and an astrophotography and optics calculator called
OptiCalculator. The calculators were initially
developed for my use. I am always on the hunt to find new formulas and features to add to my calculators.
RFCalculator had a cavity resonance section, but it was incomplete. It had a rectangular cavity with
partial dielectric fill (PCB) and cylindrical cases that needed work and did not perform the Q calculations.
The more general solutions for the cylindrical and rectangular prism cases was always preferred, but
I saw a lot of work and time to resolve and understand all the information and glean a solution. Life's
conditions had to be ripe for the effort. I had some employment uncertainties for a couple of months,
so I used the time off to do some special projects while looking for more employment. It was good challenging
mental work and kept me occupied and purposed. I had to complete the complex and S-parameter library
and functions first. I was able to complete all that sizable effort and finish a salable LabVIEW and
C language DLL library to sell for the libraries. I could now tackle the Q.
Research for the effort began with a reference search to see what material I could come up with.
In the old days searching meant at the book stores, libraries with index cards, books, magazines and
microfilm. All of them were very time consuming and book purchases were very expensive. Today, a literature
search with the Internet takes only seconds. This is a tremendous resource for the paper-challenged
(remote locations w/o books). Going to the library or bookstore used to be easy and cheap, but now with
living in the backcountry, distance costs a lot. So, I now order new or used books from Amazon for pennies
to dimes on a dollar for some very good used reference books. With Amazon, I found if I added the expensive
ones to my wish list, I would see the occasional used deals that allowed me to purchase the odd book
for my library for less. I had to be quick for these short flash gems of bound paper. They usually go
fast. Just yesterday I was able to finally purchase the Microwave Filters, Impedance-Matching Networks,
and Coupling Structures book by Matthaei, Jones and Young for $49.99 instead of the usual $119.
My Internet searches not only scan for book or article titles, but also content in them. eBay, Google,
Amazon and a slew of companies now deal in used books and a lot of classic technical books that are
coming available for very cheap prices as libraries dump their old books. I use this extensively now
to grow my engineering and science reference library. The public loss is my gain.
I purchased what reference books I could afford. Many of my engineering friend's libraries were scoured
and book loans were secured. The search was on to find the general solution for Q of rectangular prisms
and cylinders and almost no avenue was left unturned. Initial searches thru the microwave reference
books were fair, but showed many poor and incomplete examples for Q formulas that did not cover all
the cases for TE and TM modes, so the search continued.
For the rectangular prism resonant cavity the coordinates for x, y and z is a-length, b-width and
d-height. Other authors use different dimensional symbols and this can confuse novices (like me) on
the topic due to many using mode orders (l, m, n) or (m, n, L) and then l for height (Pozar). It quickly
gets very confusing. In addition to the dimensions of the cavity a few other things must be determined
to perform all the calculations leading up to the Q formulas. We need the type of metal or other surface
(like the earth for instance in the spherical case). I also use the metric system of measurements. Matthaei,
Jones and Young's book or MJY, as I will refer to it, uses English inch units and also fixes a constant
instead of showing the full formulation. Pozar's book has one formula each for the rectangular and cylindrical
case. They did not compute well at many instances outside his singular examples. Other books showed
a blithering array of variations of the coordinate systems and formulas. Most authors' examples were
singular and poorly expounded in most cases, almost as if offhanded, disappointing to be sure.
I kept gathering my reference materials and looking it over occasionally when I was bored, usually
when the weather was bad or it got dark early in winter. I kept trying Google searches to see what I
could find and discovered that search phrases could bring big differences in the search results. I was
also finding a lot of protected content on the MTT, Journal of Applied Physics and many other more obscure
sites and other references too numerous to mention. They only showed partial content if any.
One day while Web searching, I finally stumbled on the first of the Bell System Technical Journal
or BSTJ notes in the references. I had been using Cavity Resonance Q and Microwave Cavity Q in my searches
to no avail. I then tried a different variation on search string and used Microwave Cavity Testing and
there was a paper from “BSTJ” and had volume numbers on them. The two papers had the same Applied Physics
Journal table of formulas, see figure 1. I found out later that these papers were from Bell System Technical
Journal and that they had the tables, formulas and charts that helped a lot. I now had at least three
independent references for the full general Q methods to use for the various mode cases. Several of
the links to this and other referenced papers are only available to subscribers. I happen to find a
site or so that had the PDF copies available. I also found several related references from the same
Bell Systems Technical Journal which I was also able to find copies of.
These references had the same copy of the table of cavities and there reference formulas. Rectangular
had 5 total cases, the cylindrical had three cases and the coaxial has three cases. I was seeing cross
agreement with MJY for the rectangular and Collin's formulas for cylindrical. I also found a reference
to the full tables in the Microwave Engineer's Handbook Volume 1. The coaxial case was where the only
difference occurred. Also the BSTJ had the full formulation and in metric units, so the formulas had
no constants other than expected physical constants.
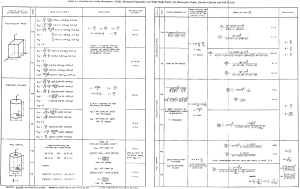
Figure 2 - Cavity Formulas
The next step was to work up the formulas and test them. I used
Mathematica for the formulation and testing. It was easy to enter the formulas and
test them. I made some changes to the variables to help me cross over to several authors' formulas simultaneously.
They needed to be tested over the range of typical values. I was successful at this stage and was starting
to notice trends in the values calculated and whether they were consistent over TM/TE modes and modal
states. All the most significant resonant cases were run for testing the Q formulas against each other,
and results were gathered. I still had the problem of determining how could I better test my values
to know if the ranges I was seeing were reasonable? I had just a few examples from the books and articles
to go by, but wanted better data. The MJY reference gives the Q as a compound function. The charts are
difficult to interpret. Re-reading thru all the references again I found some statements in Collin's
book “Foundations of Microwave Engineering”. He gave the expected range for cylindrical cavity as 10000
to 40000 with wavelengths in the 3cm range as having optimal Q. He also gave a 3x3x3cm cube in copper
Q as 12700. My calculations produced 12734.3 (see Figure 2). I was beginning to have some level of confidence
in the calculations.
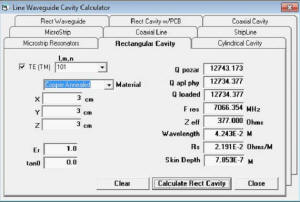
Figure 3 - 3x3x3 cm Rectangular Cavity
After all the formulas had been tested in Mathematica, I next performed the coding and testing in
my RF Calculator program. I had to work out an interface for the mode options and present them in a
easy to understand and use format. This also required looking further into the TE and TM modes and the
most commonly used modal orders so I could bring some containment to the interface, yet provide a wide
selection. I also had to allow the user to select between the surface material and the tangent loss
and dielectric constant.
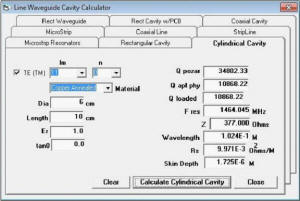
Figure 4 – Rectangular Cavity screen
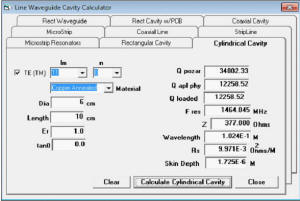
Figure 5 – Cylindrical Cavity screen
As can be seen in the screenshots answers are provided to a number of cavity values like the wavelength,
sheet resistivity, characteristic impedance and the skin depth along with the loaded and unloaded cavity
Q, resonant frequency and both the Applied Physics value for Q from BSTJ and the Pozar value for Q.
Loaded Q uses the formula 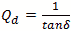 for the Q of the dielectric in the cavity.
Adding this in parallel with the cavity Q produces the total Q.
for the Q of the dielectric in the cavity.
Adding this in parallel with the cavity Q produces the total Q.
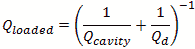
Rectangular Prism Cavity
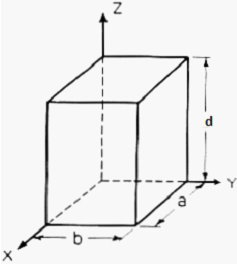
Figure 6 - Rectangular Prism Cavity
The formulas for the power are complex integrals of three dimensions. For the electric field the
formula is
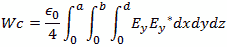
Or for the magnetic fields
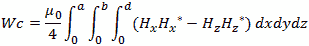
For the rate of loss or just “loss” we use the skin depth calculated below
Resistivity of copper is ρ=5813000 mhos/meter or S/m.
μo =4π10-7 H/meter
Characteristic impedance Z or 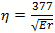 Ohms
Ohms
Sheet resistivity or 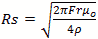 Ohms/Square
Ohms/Square
Skin depth or 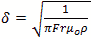 cm
cm
We calculate by defining the coordinates, dimensions, modes and mode orders x=a; y=b and z=d.
The corresponding mode orders are l, m and n for the x, y and z axis and a, b and d length. We are calculating
for a half cycle or half wavelength.
The definitions used for the calculation 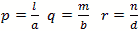
Wavelength or 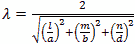 cm
cm
Resonant Frequency 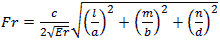 Hz
Hz
For TE mode order l, m > 0
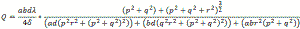
For TE mode order l = 0
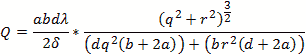
For TE mode order m = 0
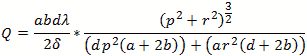
For TM mode order n > 0
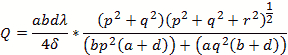
For TM mode order n = 0
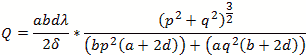
Rectangular Modes Table
The table shows the various rectangular cavity modes and mode orders as functions of the dimensions
and frequency.
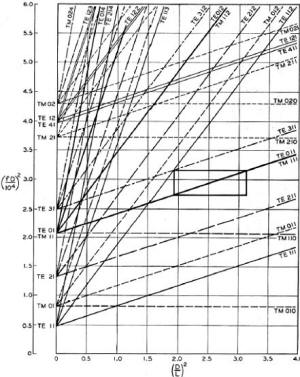
Figure 7 - Rectangular Cavity Models Chart
Cylindrical Cavity
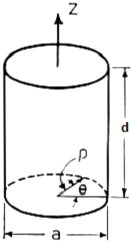
Figure 8 - Cylindrical Cavity
The formula for the cylindrical cylinder power is a complex integral of 3 dimensions.
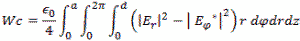
For the rate of loss or “loss” we use the skin depth calculated below
Resistivity of copper is ρ=5813000 mhos/meter or S/m
μo =4π10-7 H/meter
Characteristic impedance Z or 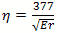 Ohms
Ohms
Sheet resistivity or 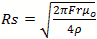 Ohms/Square
Ohms/Square
Skin depth or 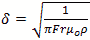 cm
cm
We again calculate using the coordinate, dimensional mode and mode order definitions. The diameter=a
and the height or z=d.
The corresponding mode orders are l, m and n for the x, y and z axis and a diameter and d length.
The l and m mode orders are not addressed the same for cylindrical cavities. For these, the zero order
Bessel J0 for the TM modes and first derivative (prime) Bessel Jp0 are used for the TE modes. These
Bessel zero values can be looked up in mathematical tables. See table in figure 8. In this case the
J0 and Jp0 values are interspersed and marked by the E or M mode and the mode order from lowest order
out to 180th order.
For TE mode
The definitions used for the calculation
Wavelength or 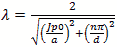 cm
cm
Resonant frequency 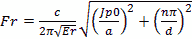 Hz
Hz
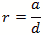
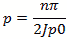
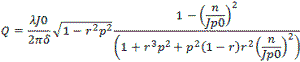
For TM mode
The definitions used for the calculation
Wavelength or 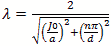
Resonant frequency 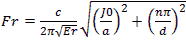
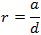
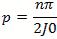
when mode order n>0
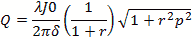
when mode order n=0
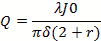
Cylindrical Modes Table of Bessel Functions
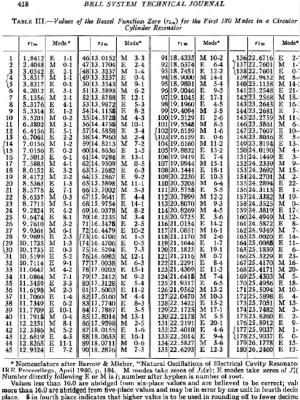
Figure 9 - Cylindrical Modes Table of Bessel Functions
Corrections for Q
Q is a complex thing and is comprised not only of the power storage/loss mechanism Qe , but also
by other effects. Dielectric materials used for cavity fill can cause a power loss resulting in
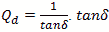 is the dielectric tangent loss. Another
Q factor is the surface roughness Qs and finally Qp is any perturbations to the geometry
such as a small aperture and electric probe wire. These addition Q factors are summed by the parallel
sum method.
is the dielectric tangent loss. Another
Q factor is the surface roughness Qs and finally Qp is any perturbations to the geometry
such as a small aperture and electric probe wire. These addition Q factors are summed by the parallel
sum method.
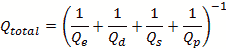
Coaxial, Spherical and other Cases
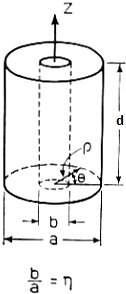
Figure 10 – Coaxial Cylinder
The coaxial cylinder case can be seen in the BSTJ documents and is quite lengthy. I have not yet
tackled that or the spherical and elliptical cases. In the article “Redefining the Kelvin” an elliptical cavity was used to get a very accurate value
for the Kelvin and Boltzmann's constant (k). For the spherical cavity case, in
Lecture Notes 10.5 they discuss the Earth's spherical resonance with Lightening
stimulation. The reader can pursue further studies in these areas if they desire. Maybe the next long
bout of extended time off and bad weather I will tackle the coaxial and spherical Q cases. For now I
am satisfied having resolved the rectangular and cylindrical cases to add to my calculator functions.
I would like to thank you the reader for allowing my indulgence with “Searching for the Q”.
References
Links
Books
- Fields and Waves in Communication Electronics; Ramo, Whinnery and Van Duzer; Wiley; iSBN
- Foundations of Microwave Engineering; Collin;Wiley; ISBN: 978-81-265-1528-8
- Microwave Engineering; Ishi; Harcourt, Brace and Jovanovich; ISBN: 0-15-558658-0
- Microwave Engineering; David M Pozar; Wiley; ISBN: 9971-51-263-7
- Microwave Engineers Handbook; Artech House; ISBN:0-89006-002-9
- Microwave Engineering and Applications; Om P. Gandhi;Pergamon Press; ISBN: 0-08-025588-4
- ARRL UHF/Microwave Experimenters Manual; ARRL; 0-87259-312-6
- Microwave Filters, Impedance-Matching Networks, and Coupling Structures, Matthaei, Jones and Young
Papers and/or Articles
- Package Resonance and Field Leakage, R. N. Simons
- Techniques Engineers the Cavity Resonance in Microstrip housing design; Edwin F. Johnson; Pacific
Monolithics; MSN & CT Feb 1987
- Predict Resonance of Shielded PCBs, Vinash Sharma; Microwaves & RF July 2007 and Aug 2007
- Design Guidelines for Microwave Cavities; Triquint Product Application Note March 2002
- EEstimation of Q-factors and Resonant Frequencies; IEEE Trans on Microwave Theory and Tech. Vol51
No. 3 March 2003
Featuring: Test Automation Services, RF Calculator
and S-Parameter Library (DLL & LLB)




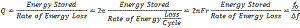
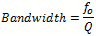





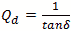 for the Q of the dielectric in the cavity.
Adding this in parallel with the cavity Q produces the total Q.
for the Q of the dielectric in the cavity.
Adding this in parallel with the cavity Q produces the total Q.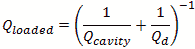

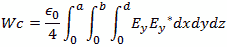
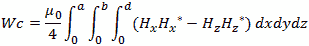
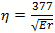 Ohms
Ohms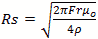 Ohms/Square
Ohms/Square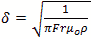 cm
cm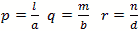
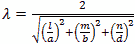 cm
cm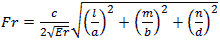 Hz
Hz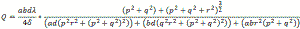
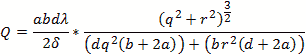
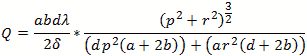
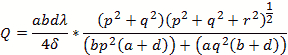
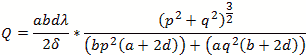


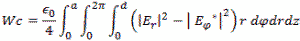
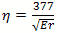 Ohms
Ohms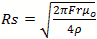 Ohms/Square
Ohms/Square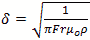 cm
cm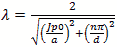 cm
cm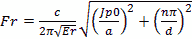 Hz
Hz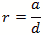
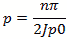
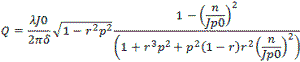
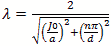
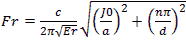
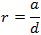
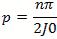
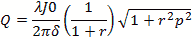
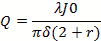

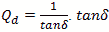 is the dielectric tangent loss. Another
Q factor is the surface roughness Qs and finally Qp is any perturbations to the geometry
such as a small aperture and electric probe wire. These addition Q factors are summed by the parallel
sum method.
is the dielectric tangent loss. Another
Q factor is the surface roughness Qs and finally Qp is any perturbations to the geometry
such as a small aperture and electric probe wire. These addition Q factors are summed by the parallel
sum method.