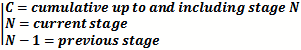
Graph of P1dB, IP2, IP3, and Saturation
See cascade calculations for NF, IP2,
IP3, and P1dB.
|
When operating within the linear region of a component, gain through that component is constant for a given frequency.
As the input signal is increased in power, a point is reached where the power of the signal at the output is not
amplified by the same amount as the smaller signal. At the point where the input signal is amplified by an amount
1 dB less than the small signal gain, the 1 dB Compression Point has been reached. A rapid decrease in gain will
be experienced after the 1 dB compression point is reached. If the input power is increased to an extreme value,
the component will be destroyed.
P1dBoutput = P1dBinput + (Gain - 1) dBm
Passive, nonlinear components such as diodes also exhibit 1 dB compression points. Indeed, it is the nonlinear
active transistors that cause the 1 dB compression point to exist in amplifiers. Of course, a power level can be
reached in any device that will eventually destroy it.
A common rule of thumb for the relationship between the 3rd-order intercept point (IP3) and the 1 dB compression
point (P1dB) is 10 to 12 dB. Many software packages allow the user to enter a fixed level for the P1dB to be below
the IP3. For instance, if a fixed level of 12 dB below IP3 is used and the IP3 for the device is +30 dBm, then the
P1dB would be +18 dBm.
 In
order to test the theory, IP3 and P1dB values from 53 randomly chosen amplifiers and mixers were entered into an
Excel spreadsheet (see
table below and resulting graph to the right). The parts represent a cross-section of silicon and GaAs,
FETs, BJTs, and diodes, connectorized and surface mount devices. A mean average and standard deviation was calculated
for the sample. In
order to test the theory, IP3 and P1dB values from 53 randomly chosen amplifiers and mixers were entered into an
Excel spreadsheet (see
table below and resulting graph to the right). The parts represent a cross-section of silicon and GaAs,
FETs, BJTs, and diodes, connectorized and surface mount devices. A mean average and standard deviation was calculated
for the sample.
As it turns out, the mean is 11.7 dB with a standard deviation of 2.9 dB, so about 68% of the sample has P1dB
values that fall between 8.8 dB and 14.6 dB below the IP3 values. What that means is that the long-lived rule of
thumb is a pretty good one. A more useful exercise might be to separate the samples into silicon and GaAs to obtain
unique (or maybe not) means and standard deviations for each.
An interesting sidebar is that where available, the IP2 values were also noted. As can be seen in the chart,
the relationship between IP2 and P1dB is not nearly as consistent.
Of equal motivation for the investigation was the desire to confirm or discredit the use of the noise figure
and IP3 type of cascade formula for use in cascading component P1dB values. As discussed elsewhere, the equation
for tracking a component from its linear operating region into its nonlinear region is highly dependent on the entire
circuit structure, and one model is not sufficient to cover all instances. Indeed, the more sophisticated (pronounced
“very expensive”) system simulators provide the ability to describe a polynomial equation that fits the curve of
the measured device. Carrying the calculation through many stages is calculation intensive. Some simulators exploit
the rule of thumb of IP3 versus P1dB tracking and simply apply the IP3 cascade equation to P1dB. As with other shortcuts,
as long as the user is aware of the approximation and can live with it, it's a beautiful thing.

Click here to view an example of a cascaded system. |
Calculating the cascaded values for 1 dB compression point (P1dB) for the system
budget requires use of ratios for gain and power levels for P1dB (do not use dB and dBm values,
respectively). The standard format for indicating decibel values is to use upper case letters; i.e.,
P1dB for units of dBm. The standard format for indicating power values is to use lower case letters; i.e.,
p1db for units of mW.Conversions: p1db = 10P1dB/10 ↔ P1dB
(dB) = 10 * log10 (p1db)
where p1db has units of mW and P1dB has units of dBm

A Typical Chain of Cascaded Components
|
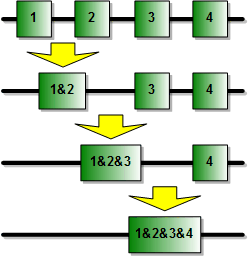
Combining 2 Stages at a Time for Calculations
|
Cascading of 1 dB Compression points is not a straightforward process, since the curve followed from linear operation
into saturation is dependent upon the circuit characteristics. A precise calculation requires knowing the equation
of the input/output power transfer curve of each device, which is typically a high-order polynomial that would be
very difficult both to ascertain and also to apply mathematically. A well-known rule-of-thumb is to subtract 10 to 15
dB to the IP3 value to estimate the P1dB value. To test that theory, I looked at the published values of IP3 and
P1dB for some common devices and calculated the difference between IP3 and P1dB (see table below). A sample of 53
devices resulted in a mean difference of 11.7 dB, with a standard deviation of 2.9 dB. That is pretty
good agreement with the rule-of-thumb.
Accordingly, a reasonable estimate of the cascaded P1dB value is to either apply the
cascaded IP3 equation directly to each device's P1dB value, or to simply calculate the actual cascaded IP3 and
subtract
10 to 15 dB to the result and declare that to be the cascaded P1dB. Note that this estimate only holds when none
of the stages in the cascade are normally operating outside of the linear region.
This equation gives the method for calculating cascaded output p1db
(op1db) values based on the equation for oip3 and gain of each stage. When using the
formula in a software program or in a spreadsheet, it is more convenient and efficient to calculate each successive
cascaded stage with the one preceding it using the following format, per the drawing (above-right).

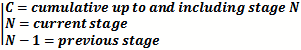

These formulas are used to convert back and forth between input- and output-referenced P1dB values:
P1dBOutput = P1dBInput + (Gain - 1) dBm
P1dBInput = P1dBOutput - (Gain - 1) dBm
The following table of values was used to create the chart shown near the top of the page.
| Amp |
Amplifonix |
2001 |
36 |
32 |
17 |
19 |
15 |
| Amp |
Amplifonix |
8701 |
47 |
35 |
25 |
22 |
10 |
| Amp |
Amplifonix |
5404 |
43 |
33 |
22 |
21 |
11 |
| Amp |
Couger/Teledyne |
A2C5119 |
46 |
33 |
19 |
27 |
14 |
| Amp |
Couger/Teledyne |
A2C4110 |
54 |
34 |
21.5 |
32.5 |
12.5 |
| Amp |
Couger/Teledyne |
A2CP14225 |
54 |
40 |
28 |
26 |
12 |
| Mixer |
Couger/Teledyne |
MC1502 |
35 |
12 |
|
35 |
12 |
| Amp |
Mimix Broadband |
CMM-4000 |
39 |
29.5 |
19 |
|
10.5 |
| Amp |
Mimix Broadband |
CMM-1110 |
31 |
22 |
13 |
|
9 |
| Amp |
M/A-COM |
A101 |
64 |
36 |
23 |
41 |
13 |
| Amp |
M/A-COM |
A231 |
25 |
22 |
10 |
15 |
12 |
| Amp |
M/A-COM |
AM05-0005 |
55 |
37 |
23 |
32 |
14 |
| Amp |
M/A-COM |
SMA411 |
32 |
24 |
10 |
|
14 |
| Mixer |
Polyphase |
IRM0714B |
67 |
15 |
7.6 |
|
7.4 |
| Mixer |
Polyphase |
IRM1925B |
68 |
14 |
8 |
|
6 |
| Mixer |
Amplifonix |
M53T |
|
13 |
3.5 |
|
9.5 |
| Amp |
JCA |
JCA01-301 |
|
20 |
13 |
|
7 |
| Amp |
JCA |
JCS02-332 |
|
33 |
23 |
|
10 |
| Amp |
Mimix Broadband |
XL1005 |
|
24 |
16 |
|
8 |
| Amp |
Technology Distribution |
0600-0007 |
|
25 |
10 |
|
15 |
| Amp |
Technology Distribution |
0600-0025 |
|
20 |
15 |
|
5 |
| Amp |
Technology Distribution |
0600-0024A |
|
30 |
12 |
|
18 |
| Amp |
Stealth Microwave |
SM3436-34HS |
|
47 |
34 |
|
13 |
| Amp |
Stealth Microwave |
SM1925-33 |
|
47 |
33 |
|
14 |
| Amp |
M/A-COM |
MAALSS0045 |
|
32 |
20 |
|
12 |
| Mixer |
M/A-COM |
CSM1-10 |
|
19 |
6 |
|
13 |
| Mixer |
M/A-COM |
M5T |
|
18 |
7 |
|
11 |
| Mixer |
Marki Microwave |
M1-0204L |
|
12 |
2 |
|
10 |
| Mixer |
Marki Microwave |
M1R-0726M |
|
15 |
5 |
|
10 |
| Mixer |
Polyphase |
SSB2425A |
|
19 |
8 |
|
11 |
| Amp |
Triquint |
TGA2512-SM |
|
16 |
6 |
|
10 |
| Mixer |
Triquint |
CMY 210 |
|
24 |
14 |
|
10 |
| Amp |
Miteq |
AFS3-00500200-27P-CT-6 |
|
38 |
27 |
|
11 |
| Amp |
Milliwave |
TMT4-060-180-35-10P-2 |
|
20 |
10 |
|
10 |
| Amp |
Milliwave |
TMT6-500-750-100-5P-5 |
|
14 |
5 |
|
9 |
| Amp |
Milliwave |
AMT4-060-180-40-10P-1 |
|
22 |
15 |
|
7 |
| Amp |
Skyworks |
SKY65013-70LF |
|
29 |
14 |
|
15 |
| Amp |
Skyworks |
SKY65015-92LF |
|
35 |
18 |
|
17 |
| Mixer |
Synergy |
FSM-2 |
|
40 |
23 |
|
17 |
| Mixer |
Synergy |
SGM-2-17 |
|
18 |
10 |
|
8 |
| Amp |
Microwave Technology |
MwT-A989 |
|
39 |
24 |
|
15 |
| Amp |
Hittite |
HMC376LP3 |
|
36 |
21.5 |
|
14.5 |
| Amp |
Hittite |
HMC564 |
|
24 |
12 |
|
12 |
| Mixer |
Hittite |
HMC399MS8 |
|
34 |
24 |
|
10 |
| Amp |
RFIC |
RFISLNA01 |
|
24 |
14 |
|
10 |
| Amp |
RFMD |
NBB-302 |
|
23.5 |
13.7 |
|
9.8 |
| Amp |
RFMD |
RF2878 |
|
29 |
14.4 |
|
14.6 |
| Amp |
NuWaves |
NILNA-GPS |
|
31 |
17 |
|
14 |
| Amp |
MCL |
AMP-15 |
|
22 |
8 |
|
14 |
| Amp |
MCL |
ZFL-500HLN |
|
30 |
16 |
|
14 |
| Amp |
MCL |
ZQL-900LNW |
|
35 |
21 |
|
14 |
| Mixer |
MCL |
MCA-19FLH |
|
25 |
10 |
|
15 |
| Mixer |
MCL |
MCA-1-12GL |
|
9 |
1 |
|
8 |
|
|
|
|
|
Mean |
27.1 |
11.7 |
|
|
|
|
|
StdDev |
8.1 |
2.9 |
|
|
|
|
|
Samples |
10 |
53 |
|