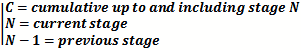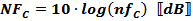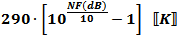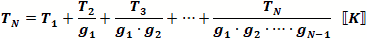|
Noise figure (NF) is the increase in noise power of a device from the input to the output that is greater than
the signal gain. In effect, it is the amount of decrease of the signal-to-noise ratio. Like gain, noise figure can
be expressed either as a ratio or in decibels (dB). Note: NF is not a power level, so
it never has units of dBm.
As the following equation shows, cascaded noise figure is affected most profoundly by the noise figure of components
closest to the input of the system as long as some positive gain exists in the cascade. If only loss exists in the
cascade, then the cascaded noise figure equals the magnitude of the total loss.

Click here to view an example of a cascaded system. |
Calculating the cascaded values for noise figure (NF) for the system budget requires the following operation based
upon ratios for gain and noise figure (do not use decibel values). The standard format for indicating decibel values
is to use upper case letters, i.e., G and NF for units of dB; the standard format for indicating ratio values is
to use lower case letters, i.e., g and nf.
Conversions: nf = 10NF/10 ↔ NF
(dB) = 10 * log10 (nf)
where nf is a unitless ratio and NF has units of dB
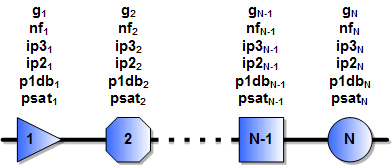
A Typical Chain of Cascaded Components
|

Combining 2 Stages at a Time for Calculations
See cascade calculations for NF, IP2, IP3, and
P1dB.
|
This equation gives the method for calculating cascaded NF (nf) values based on the nf and gain of each stage.
When using the formula in a software program or in a spreadsheet, it is more convenient and efficient to calculate
each successive cascaded stage with the one preceding it using the following format, per the drawing
(above-right).

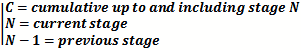
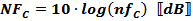
Click here to see Agilent's
App Note 1303 on using a spectrum analyzer to measure noise figure.
Noise Temperature (K) =
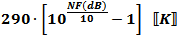
Noise Figure (dB) =

These equations assume a room temperature reference (290 K). If applicable, use whatever
your reference temperature is in place of the 290K shown.
Cascaded Noise Temperature Calculation
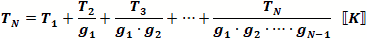
The following table lists a few conversions. See the Noise Power
Calculator online calculator
for calculating other values.
| 0.1 |
7 |
2.1 |
180 |
| 0.2 |
14 |
2.2 |
191 |
| 0.3 |
21 |
2.3 |
202 |
| 0.4 |
28 |
2.4 |
214 |
| 0.5 |
35 |
2.5 |
226 |
| 0.6 |
43 |
2.6 |
238 |
| 0.7 |
51 |
2.7 |
250 |
| 0.8 |
59 |
2.8 |
263 |
| 0.9 |
67 |
2.9 |
275 |
| 1.0 |
75 |
3.0 |
289 |
| 1.1 |
84 |
3.1 |
302 |
| 1.2 |
92 |
3.2 |
316 |
| 1.3 |
101 |
3.3 |
330 |
| 1.4 |
110 |
3.4 |
344 |
| 1.5 |
120 |
3.5 |
359 |
| 1.6 |
129 |
3.6 |
374 |
| 1.7 |
139 |
3.7 |
390 |
| 1.8 |
149 |
3.8 |
406 |
| 1.9 |
159 |
3.9 |
422 |
| 2.0 |
170 |
4.0 |
438 |
|
 |
Related Pages on RF Cafe -
Noise Figure <--> Noise Temperature
Calculator - Noise Power and Voltage -
Cascaded Noise Figure -
Noise Figure Meters & Noise Generators -
Noise Sources
Check
this out - someone referenced this page on
Wikipedia!
|