September 1942 QST
 Table
of Contents Table
of Contents
Wax nostalgic about and learn from the history of early electronics. See articles
from
QST, published December 1915 - present (visit ARRL
for info). All copyrights hereby acknowledged.
|
It's hard for most people alive today
to imagine a time when vacuum tubes were the only means of amplification and
rectification available. The discovery and application of semiconductors as
replacements was a huge step forward for all but the highest power applications
like megawatt power amplifiers. Equally hard to imagine is having to design
circuits without the aide of computers - or at least a digital calculator. Parameter
tables and slide rules were de rigueur for the day. Power supplies in the hundreds
of volts were commonplace and printed circuit boards were a platform of the
future. Point-to-point wiring ruled the day.
Other than for special cases like traveling wave tubes (TWTs) and microwave
magnetrons, there are not many engineers left that design tubes. As with a lot
of the vintage methods and equipment, it is amateur hobbyists who keep the art
of tube circuits alive. The Internet is full of projects and articles on tube
design. I have accumulated a few resources over the years right here on RF Cafe.
NOTE: References to the Handbook in the Assignments are for the ARRL Handbook
of the day. Sorry, I don't have that available.
A Course in Radio Fundamentals
Lessons in Radio Theory for the Amateur By George
Grammer, W1DF
No.4 - Vacuum-Tube Fundamentals

Fig. 1 - Vacuum tube board.
Experiments designed to show comprehensively the operation of the vacuum
tube as an amplifier require a fairly elaborate array of test apparatus. Finding
the gain-frequency characteristic of an audio amplifier, for example, requires
the use of a calibrated source of variable frequency over the audio-frequency
range, plus a calibrated attenuator and means for measuring voltage with readings
independent of frequency, while distortion cannot readily be observed without
an oscilloscope. Such equipment is expensive and satisfactory substitutes cannot
readily be constructed at home.
However, simple experiments designed to show the properties of vacuum tubes
readily can be performed with the gear described in the preceding installments.
As a convenience in setting up apparatus, a tube board such as is shown in Fig. 1
can be added. It consists simply of a baseboard on which is placed a square
piece of Bakelite in which is mounted an ordinary octal socket, connections
being brought out from the socket prongs to machine-screw terminals. This permits
chanting tube connections without soldering. The heater terminals are permanently
connected to a terminal strip mounted at the back of the board; this strip also
has terminals for "B" supply, one negative and two positive. The latter take
care of separate plate and screen voltages when a tetrode or pentode is used.
A push-button mounted on the board provides a means of closing the plate (or
screen) circuit when the milliammeter in the test instrument is being used for
other measurements.
In using the plate power supply with its variable voltage divider it should
be remembered that only a limited current can be taken through the divider taps
for more than very short periods of time. The variable resistor, in particular,
is rated at only a few watts, and if the output current is more than 15 milliamperes
or so the time during which current flows must be kept to a minimum. Since a
reading can be taken in a mat-ter of seconds this is no handicap, but if the
supply is used for continuous output the resistor arm should be set at the end
connected to the transformer center tap (see Fig. 4, p. 65, August QST),
or else a switch should be provided for shorting between the negative output
terminal and the wire connected to the center-tap of the power transformer.
Tube Characteristics
Some amplification of the Handbook material dealing with tube constants may
be helpful in connection with the experimental work. In the paragraph on "Characteristics"
(§ 3-2), for instance, plate resistance is defined as "the ratio, for a fixed
grid voltage, of a small plate voltage change to the plate current change it
effects." This can be written in the form of an equation:

where rp stands for plate resistance, ΔEp for the change
in plate voltage, and ΔIp for the corresponding change in plate current.
The sign Δ indicates that we are concerned not with one value but with the difference
between two values. (In other respects the equation is simply the familiar statement
of Ohm's Law.) The other two constants, amplification factor and mutual conductance,
also can be defined in formulas instead of words:
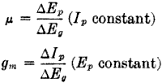
By simple substitution in these formulas it is found that the three constants
are related in this way:

The values of the constants can be found by plotting characteristic curves
and measuring the change which occurs in one quantity when the other is changed
any arbitrary amount. However, this method must be used with some caution when
the characteristic curve does not turn out to be a straight line. If the line
bends, the "constant" is not actually always the same, but varies with the point
on the curve at which it is measured. For example, suppose that Fig. 2
represents a curve showing the variation of plate current as the plate voltage
is varied, and from it we want to determine the plate resistance. We arbitrarily
select A as the point from which to start and, also arbitrarily, decide to make
the plate current change, Ip 2 milliamperes. A 2-milliampere increase
brings us to point B on the curve. Then the corresponding change in plate voltage,
Ep, is the difference between the plate voltages which cause 1 and
3 milliamperes to flow. Thus Ep = 70 - 30 = 40 volts. Then

Suppose that instead of 2 milliamperes for Ip we had selected
1 milliampere. This would bring us to point C on the curve, and now Ep
= 53 - 30 = 23 volts. Substituting these new values in the equation gives us

Because of the curvature of the characteristic the value of the "constant"
rp as measured by this method will depend considerably upon the value
of Δ selected. As the value of Δ is made smaller and smaller the value of the
ratio ΔEp/ΔIp approaches the ratio AD/DE, where the line
FE is drawn tangent to the curve at point A (that is, the line FE touches but
does not intersect the curve at point A). In Fig. 2 this ratio is

which is the value of the plate resistance at point A on the curve. If points
B or C had been selected instead of A as the starting place (point at which
plate resistance is to be determined) different values of plate resistance would
be obtained, since it is obvious that tangents drawn through these points would
not coincide with the tangent EF.

Fig. 2 - Basis for measurement of ΔEp and ΔIp chart.
In determining the values of the tube constants from the curves, therefore,
the preferred procedure is to draw a tangent to the curve at the point at which
the value of the constant is to be measured, and then use the tangent line as
a basis for measurement of ΔEp and ΔIp (or whatever pair
of quantities is represented by the curve).
While there is bound to be some inaccuracy in drawing the tangent, in general
the results will be nearer the truth than if two points on the curve itself
are selected. Of course if the curve is straight the curve and its tangent coincide,
so that in the special case of a straight-line curve points can be taken directly
from the curve.
Caution
In the diagrams of the various setups for the experiments to follow, milliammeters
and volt-meters are indicated where measurements are to be made. If enough separate
instruments are at hand, they may be used as shown. However, if only the single
combination test instrument is available for measuring currents and voltages,
extreme care should be used to see that the proper range is selected before
making voltage measurements. In alternate switching from current to voltage
it is only too easy to leave the range switch on 0-1 ma. when connecting the
instrument across three or four hundred volts - with consequences easy to imagine.
Such an error - bad enough normally - would be practically fatal now, with instrument
replacements or repairs virtually impossible. Watch that range switch!
ASSIGNMENT 11 Study Handbook Sections 3-1 and 3-2,
starting page 42. Perform Exps. 21, 22 and 23.
Questions
1) How does conduction take place in a thermionic vacuum tube?
2) What is the space charge?
3) What is the purpose of the grid in a triode?
4) Name the three fundamental tube characteristics and define them.
5) Why is a "load" necessary if a vacuum tube is to perform useful
work?
6) What are tube characteristic curves?
7) Why is amplification possible with a triode tube?
8) What is meant by the term "interelectrode capacity"?
9) What is the difference between static and dynamic characteristic
curves?
10) In what form is the power supplied to the plate-cathode circuit of a
tube dissipated?
11) What is the purpose of tube ratings?
12) What is meant by the term "plate current cutoff point or"?
13) What is grid bias, and why is it used?
14) Define saturation point.
15) What is rectification?
ASSIGNMENT 12 Study Handbook Sections 3-3 and 3-4,
starting page 44. Perform Exp. 24. Questions 1) Name three
forms which the plate load for a triode amplifier may take.
2) Define voltage amplification; power amplification. What is
the essential difference between amplifiers designed for the two purposes?
3) What determines the choice of operating point for an amplifier?
4) Define plate efficiency. How does it vary with different types
of operation (Class A, B and C)?
5) What is harmonic distortion and how is it caused?
6) Describe Class-A amplifier operation.
7) What is feedback? What is the result of application of positive
feedback? Of negative feedback?
8) How is the input capacity of a triode amplifier affected by
its operating conditions?
9) What is driving power?
10) What is the phase relationship between the alternating voltage applied
to the grid of an amplifier having a resistance load and the amplified voltage
which appears in the plate circuit?
11) What is the effect of the value of load resistance on the amplification
obtainable with a given tube?
12) If a certain power amplifier circuit delivers 3.5 watts when a signal
voltage of 20 peak volts is applied to the grid, what is the power sensitivity
of the amplifier?
13) Describe Class-B amplifier operation.
14) What is the definition of a decibel?
15) If the power level at one point in an amplifier is 0.25 watt and at a
later point is 4 watts, what is the gain in db.?
16) What are the distinguishing characteristics of a Class-C amplifier?
17) What is the difference between parallel and push-pull operation?
18) A certain circuit provides an attenuation of 15 db.
What is the ratio of power levels in the circuit?
19) If a signal of 0.6 volt is applied to an amplifier having a voltage amplification
of 125, what is the output voltage?
20) In a certain amplifier an input voltage of 0.01 volt produces an output
voltage of 50 across 500 ohms. The input resistance of the amplifier is 0.1
megohm. What is the gain of the amplifier in db.?
ASSIGNMENT 13 Study Handbook Sections 3-5 and 3-6,
beginning page 48. Perform Exp. 25.
Questions 1) What is the purpose of the
screen grid in a tetrode or pentode tube intended for use as a radio-frequency
amplifier?
2) Does the shielding afforded by the screen grid have to be
as complete in a tetrode or pentode designed for audio frequency amplification
as in one designed for radio-frequency amplification?
3) Describe secondary emission.
4)How may the effects of secondary emission be reduced in a screen-grid tube?
5) What is the difference between a "variable-µ" and "sharp cut-off
H tube?
6) Why is a mercury-vapor rectifier preferred to a high-vacuum
rectifier when the rectifier tube must handle a con-siderable amount of power?
7) How does a mercury-vapor grid-control rectifier differ from
a high-vacuum triode? Could such a gas triode" be used for amplification in
the ordinary sense of the word?
8) Identify five general types of multipurpose tubes.
9) What is a beam tube?
10) Name the two general types of cathodes used in thermionic vacuum tubes.
11) What is the advantage of the unipotential cathode?
12) What is the purpose of center-tapping the filament supply of a tube whose
cathode is heated by alternating current?
13) A certain r.f. power amplifier requires a negative grid bias of 200 volts
for Class-C operation. The d.c, grid current is to be 16 milliamperes under
operating conditions. If the bias is to be obtained entirely from grid leak
action, what value of grid-leak resistance is required?
14) A triode amplifier requires a negative grid bias of 30 volts, at which
bias the plate current is 45 milliamperes. What value of cathode resistance
will give the required bias? If the amplifier is to be used at audio frequencies
as low as 100 cycles, what value of by-pass capacity should be shunted across
the resistor to minimize negative feed-back?
15) What value of cathode bias resistance should be provided for a 6F6 used
as a Class-A pentode audio amplifier with 250 volts on the plate? (Use published
operating conditions.) What value of by-pass condenser should be used to prevent
negative feed-back at frequencies down to 80 cycles?
16) A push-pull r.f. power amplifier requires 400 volts bias and a d.c, grid
current of 15 milliamperes per tube under rated operating conditions. If 130
volts of fixed bias is to be provided by batteries, what id leak resistance
should be used?
ASSIGNMENT 14 Study Handbook Section 3-7, beginning
page 50. Perform Exp. 26.
Questions 1) How may a vacuum-tube circuit
be made to generate self-sustained oscillations?
2) Can oscillations be set up in a circuit in which the feed-back
is negative?
3) What is negative resistance?
4) Define series feed; parallel feed .
5) Draw two circuits utilizing magnetic feed-back.
6) How can the amount of feed-back be controlled in the Colpitts
circuit?
7) Draw a simple triode crystal oscillator circuit. Which of
the ordinary oscillator circuits does it resemble most closely?
8) Define the plate efficiency of an oscillator.
9) Name four factors which can affect the frequency of oscillation.
10) What is a multivibrator? Name one of the uses for this type of oscillator.
11) How can the effect of plate voltage variations on frequency of oscillation
be minimized?
12) Draw three oscillator circuits with capacity feed-back, and describe
how the feed-back may be controlled in each.
13) What is the usual method of obtaining grid bias in an oscillator circuit?
Why is it used in preference to other methods?
14) How can frequency drift in an oscillator be reduced?
15) A 25-microhenry coil is available for use in an oscillator circuit which
is to operate at approximately 2000 kc, What capacity will be required to tune
the coil?
ASSIGNMENT 15 Study Handbook Sections 3-8 and 3-9,
beginning page 55.
Questions 1) What is a fluorescent screen?
2) Describe the construction and operation of a simple cathode
ray oscilloscope tube. 3) By what methods may an electron beam be
deflected?
4) Define deflection sensitivity.
5) How is the intensity of the fluorescent spot controlled?
6) What is the purpose of the sweep circuit in an oscilloscope?
7) Name two common forms of sweep. What are the advantages and
disadvantages of each?
8) What is an electron gun?
9) Why is it desirable to use amplifiers for the deflection voltages
for a cathode ray tube?
10) Why should the time of the return trace in a linear sweep circuit be
as short as possible?
11) Explain the method by which patterns are formed on the fluorescent screen.
Construct a pattern, using a. linear sweep with return trace time equal to 1/20
of the total time of the sweep cycle, for two cycles of a sine wave applied
to the vertical plates. Construct a pattern, using the same two sine-wave cycles
applied to the vertical plates, but with a single sine wave for the horizontal
sweep. Compare with the linear sweep.
12) Describe the operation of a gas-triode linear sweep generator.
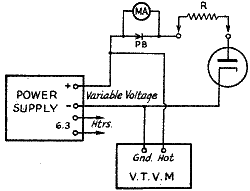
Fig. 3 - Diode circuit arrangement.
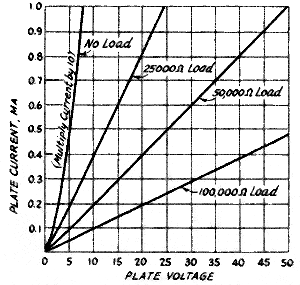
Fig. 4 - Plate current and plate voltage plot.
EXPERIMENT 21
Diode Characteristics
Apparatus: This experiment uses the plate power supply,
tube board, test set, vacuum-tube voltmeter, and three 1- watt resistors, 25,000,
50,000 and 100,000 ohms. The circuit arrangement is shown in Fig. 3. Measurements
must be made of the voltage applied to the tube and the current flowing in its
plate-cathode circuit; the single test instrument can be used for both purposes
by being shifted back and forth for each pair of readings. However, the small
current consumed by the instrument when used as a voltmeter will cause the actual
output voltage to be lower when the voltage is being measured than when the
instrument is shifted to read plate current. Unless a separate voltmeter which
can be left permanently in the circuit is available, it is advisable to use
the v.t. voltmeter, thus avoiding the loading effect. The test instrument is
therefore shifted between the plate circuit of the tube being tested and the
plate circuit of the voltmeter tube.
The tube to be tested may be a 6H6, the diode section of a combination diode-amplifier
tube, or simply a small triode such as the 6J5 with the grid and plate connected
together to act as a single plate.
Procedure: The object of the experiment is to plot characteristic
curves, plate voltage vs. plate current for the tube alone (static characteristic)
and with various values of load resistance in series with the plate circuit
(dynamic characteristics). Starting at zero plate voltage, increase the plate
voltage in small steps, taking plate current readings at each voltage step.
With no load resistor in the circuit, take readings at intervals of voltage
which will give current in-tervals of about 1 milliampere so that enough points
will be secured to give a smooth curve when the points are plotted. In the case
of the 6H6 tube, using one plate and cathode only, one-volt intervals are suitable.
Proceed similarly when the load resistance is inserted in the circuit; in this
case larger voltage intervals (5-volt steps, for instance) can be used.
In using the single test set for all measurements. the push-button should
be closed while the voltage measurement is being made so that the voltage can
be adjusted to the proper value with plate current flowing. If the plate circuit
is not closed at the time the voltage is adjusted, the voltage will drop when
the milliammeter is connected in the plate circuit of the tube to measure plate
current. It is not necessary to make provision for closing the plate circuit
of the v.t.v.m. when the meter is being used elsewhere.
The observed data should be plotted in the fashion shown in Fig. 4,
which gives characteristic curves taken on a 6H6. With no load the current is
quite high, reaching 10 milliamperes with about 7.5 volts applied. Other types
of tubes may give considerably different plate current values without load,
but should approximate the load curves given since the current which flows at
a given voltage is principally determined by the load resistance rather than
the tube. As is to be expected, the current decreases, at a given applied voltage,
as the load resistance is increased.
If the no-load curve is inspected carefully, it will be observed that it
is not a straight line, particularly near the low-voltage end. The lamp in Exp.
10 was another example of a non-linear circuit, although for a different reason.
In the present case, the nonlinearity arises from the fact that the number of
electrons drawn to the plate is not strictly proportional to the voltage applied
between plate and cathode, The d.c. resistance of the diode at any voltage is
equal to that voltage divided by the current which it forces through the tube.
In practice the behavior of the tube when an alternating voltage is applied
is of more interest, in which case the a.c, plate resistance, or resistance
effective to small changes in applied voltage, is important. The value of this
plate resistance is found as described in the introduction to this installment.

Fig. 5 - Triode test circuit.

Fig. 6 - Triode grid voltage vs. plate current.
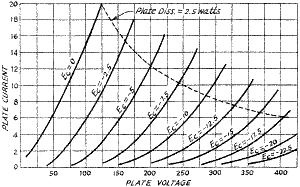
Fig. 7 - Typical grid-voltage plate-current family
taken on a 6J5.
When a load resistance is inserted in the plate circuit the linearity of
the circuit consisting of the resistance and the tube is better than that of
the tube alone. This improvement, which increases as the load resistance is
increased, is because the load resistor tends to reduce the effect of variations
in the resistance of the tube. For example, if the resistance of the tube varies
between 1000 and 3000 ohms with a
certain range of applied voltage the resistance change is 2000 ohms, or an
increase of 200%, using the smaller number as a base, If a 10,000-ohm resistor
is connected in series, the minimum resistance becomes 11,000 ohms and the maximum
resistance 13,000 ohms, so that the increase in resistance is now only 2000/11,000,
or 18%. With 100,000 ohms in series, the increase is from 101,000 to 103,000
ohms, so that the percentage increase is now 2%. In the curves of Fig. 3
the addition of the load resistance makes all the points fall on a line which
is practically straight except at the low voltage end where the tube resistance
has its highest value. The higher the load resistance the less marked does this
slight curvature become.
In taking data it will be observed that a small current flows in the plate
circuit even at zero plate voltage. This
current is the result of the fact that some electrons are emitted from the
cathode with sufficient velocity to reach the plate even though there is no
positive charge on the plate to attract them. For complete cut-off of plate
current
it would be necessary to make the plate a volt or two negative with respect
to the cathode, thus repelling these high energy electrons from the plate. Since
the current in any case is very small - a very small fraction of a milliampere
- it can be neglected in most applications of the tube. However, in flowing
through an external load resistance of high value a volt or two may be developed
across the load, which may need to be taken into account in some cases.
Experiment 22
Triode Static Characteristics Apparatus:
The set-up for this experiment is shown in Fig. 5. Insofar as the plate
circuit of the triode is concerned. the arrangement is practically the same
as that used for diode measurements, :Fig. 3, except that it is possible
to measure plate voltage with the test instrument rather than the v.t. voltmeter.
This is because larger plate voltage steps may be used so that a high range
(500 volts or the nearest provided on the test instrument), which will have
a resistance of a half megohm or so, will give sufficient accuracy for all measurement.
The bias supply is incorporated in the
set-up to provide variable grid bias, and its voltage output also may be
measured by the test instrument on the condition that the voltmeter resistance
is 25,000 ohms or so (25-volt scale). Be sure that the positive output terminal
of the bias supply is connected to the grounded side of the 115-volt line, using
the lamp provided for checking as described in July QST. In using a single instrument
in place of the three indicated, the push-button should be closed each time
the plate voltage is measured so that the voltage will be that existing when
plate current flows. The resistor R shown in Fig. 5 is not needed
in this experiment, so the push-button may be connected directly to the plate.
Procedure: The object of the experiment is to determine the
relationship between plate voltage, plate current and grid voltage of a small
triode. One quantity is held constant throughout a run, the second is varied,
and corresponding measurements of the third are made. A receiving triode such
as the 6J5 is suitable. Three sets of characteristics can be taken; the first,
with the plate voltage held fixed while the behavior of plate current with varying
grid voltage is observed, is called the "grid voltage plate current" characteristic.
When a series of such data is taken with several fixed values of plate voltage,
a "family" of curves results. A typical grid-voltage plate-current family taken
in this way on a 6J5 is shown in Fig. 6. The plate voltage was set at 50-
volt intervals from 50 to 400 volts (the maximum output voltage of the power
supply described in August QST),
enough points being taken at each plate voltage to permit smooth curves to
be drawn. Notice that for each value of plate voltage the curve bends at the
higher values of negative grid voltage (as the plate current decreases toward
the cut-off point) but that the curvature decreases as the grid bias becomes
less negative. The curves eventually straighten out and become practically parallel,
and the distances between the 50-volt intervals also approach equality. The
dashed line shows the value of plate current at which the plate dissipation
(plate voltage multiplied by plate current) is equal to the maximum rated value
for the tube; above this line the plate dissipation is exceeded. The
"plate family," shown plotted from experimental data in Fig. 7, is obtained
by holding the grid bias constant at selected values and measuring the plate
current as the plate voltage is varied. These curves show the same general tendency
to bend when the plate current is near cut-off, and to straighten out at higher
values of plate current. The plate family is frequently more useful than the
set of grid voltage-plate current curves represented by Fig. 6.
When the remaining quantity, plate current, is held constant while the grid
voltage is varied (the plate voltage being adjusted for each value of grid bias
to give the selected value of plate current) the set of curves shown in Fig. 8
results, again plotted from experimental data on a 6J5. These "constant current"
curves show the relative effect of grid voltage and plate voltage on plate current.
The curves are nearly straight lines for all except very small values of plate
current, showing that the amplification factor is practically constant for a
given plate-current value regardless of the plate and grid voltages. The fact
that, with the exception of the curve for a plate current of 0.1 milliampere,
the curves are very nearly parallel indicates that the amplification factor
also is nearly independent of the plate current so long as the latter is not
near the cut-off point.

Fig. 8 - Plate current curves for grid voltage vs.
plate voltage.

Fig. 9 - Variation in µ, rp and gm
as a function of grid bias when the plate voltage is held constant at 250 volts.
The values of amplification factor, µ, plate resistance, rp, and
mutual conductance, gm, can be measured from these three sets of
curves. The mutual conductance, ΔIpΔEg can be found from
the curves of Fig. 6 since these curves show the relationship between grid
voltage and plate current. The plate resistance, ΔIp/ΔEp,
can be measured from the curves of Fig. 7, which relate plate current to
plate voltage for various values of grid bias, while the amplification factor
ΔIpΔEg, can be taken from the curves of Fig. 8.
The method of making these measurements is described in the introduction to
this installment. Since these "constants" are a function of three variables
a large number of graphs would be required to give their behavior even partially
completely, but one special case is shown in Fig. 9. This graph shows the
variation in µ, rp and gm as a function of grid bias when
the plate voltage is held constant at 250 volts, the normal rated operating
voltage for the tube, and is a plot of values measured at 250-volt points on
each of the three sets of curves in Figs. 6, 7 and 8. It is plain that the amplification
factor changes relatively little compared to the changes in the other two quantities.
Increasing negative grid bias causes
the mutual conductance to decrease, which means that the amplification obtainable
from the tube also decreases since amplification is proportional to mutual conductance,
other things being equal. On the other hand, the plate resistance increases
with increasing negative grid bias. As a check on the accuracy of measurement,
the three curves should satisfy the relationship

within reasonable limits of accuracy, for any given value of grid bias. If
published average curves for the type of tube measured are available, it will
be of interest to compare them to the curves determined experimentally. Exact
duplication of the published curves is not to be expected, of course, because
of slight variations in manufacture.
EXPERIMENT 23
Triode Dynamic Operation Apparatus:
Same equipment as for Exp. 22, with the addition of the following resistors:
5000, 10,000, 25,000, 50,000 and 100,000 ohms. Resistors of 1-watt rating will
be satisfactory. Procedure: The object of this experiment
is to plot dynamic grid voltage-plate current characteristics for representative
values of plate load resistance. Using a fixed value of plate-supply voltage,
insert a resistor at R, Fig. 5, and measure the plate current as the grid
bias is varied in steps of 2.5 volts or so. Each time the grid bias is changed,
readjust the plate-supply voltage (measured across the
supply terminals, not from plate to cathode of the tube being investigated)
with the push-button closed so that the voltage under load will be the actual
value selected. The voltage will need to be re-set as the plate current increases,
because of voltage drop in the power supply. When a complete set of data has
been obtained with one value of plate load resistance, change to another value
and take another run. When finished with all values of resistance, plot the
data in the form of curves showing plate current against grid bias.
A typical set of such curves, taken on a 6J5 with the plate voltage constant
at 300, is shown in Fig. 10. As the plate load resistance is made larger
the maximum plate current (at zero grid bias) becomes smaller, as is to be expected.
The plate current cutoff point, however, occurs at approximately the same value
of negative grid bias in each case, since the plate voltage is fixed and at
zero current there is no voltage drop in the load resistor. As in the case of
the diode which was the subject of Exp. 21, increasing the value of load resistance
has the effect of straightening out the curve, so that the curves taken with
high values of load show less bending than curves with no load or small values
of load resistance.
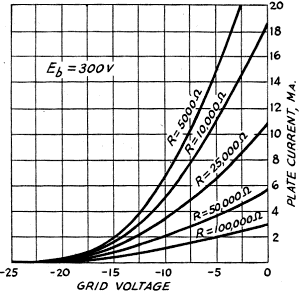
Fig. 10 - 6J5 with the plate voltage constant at 300
volts.

Fig. 11 - Two halves of the plate current cycle are
not exactly the same shape.

Fig. 12 - Current flowing in the plate circuit will
cause a voltage drop across the load resistance.
The effect of the load resistance on the amplification obtainable from the
tube, and also the distortion it introduces, can be found graphically from curves
such as these. In Fig. 11, as an illustration, the curve for R = 10,000
ohms has been plotted singly for the purpose of showing the relationship between
varying grid signal voltage and the corresponding variations in plate current.
An operating point should be chosen somewhere near the middle of the relatively-straight
part of the curve, such that the product of the plate current by the voltage
between plate and cathode
will not exceed the rated plate dissipation of the tube. In Fig. 11
the operating point selected is the point A, at -7.5 volts grid bias, making
the no-signal plate current slightly less than 8 milliamperes. The dashed line
extending downward from A is the axis of grid voltage, and the line extending
to the right is the axis of plate current. On the grid voltage axis a sine wave
is plotted as the assumed signal voltage (the actual shape of the signal wave
is not highly important, but the sine wave is representative of a single frequency)
as a function of time, one complete cycle being represented. In Fig. 11
the signal has a maximum amplitude of 5 volts, so that the instantaneous grid
voltage swings between the limits of -2.5 volts and -12.5 volts about the fixed
grid bias of -7.5 volts. A corresponding time scale is applied to the plate
current axis so that the plate current corresponding to the grid voltage at
a given instant can be plotted.
At zero time (beginning of the cycle) the grid voltage is -7.5 and the plate
current 7.8 ma., approximately, One-eighth cycle later (point B) the grid signal
voltage has risen to 71 % of its maximum value so that the instantaneous grid
voltage is -4 volts. The plate current, C, at that same instant is 12.3 milliamperes,
and this value is plotted at D, one-eighth cycle from zero time on the plate-current
axis. Points for other instants are similarly obtained until enough are plotted
to permit drawing a smooth curve. When the cycle is complete it can be compared
for shape to the original grid signal. As Fig. 11 shows, the two halves
of the plate current cycle are not exactly the same shape, as they were in the
grid signal. This difference in shape represents distortion, and the greater
the difference the more distortion there is present. As is obvious from the
drawing, the distortion is caused by the curvature of the tube characteristic,
since if the characteristic were perfectly straight the plate current would
be proportional to the grid voltage. Plotting similar graphs from dynamic curves
taken with different values of load resistance readily will show the effect
of the load resistance on distortion. The gain of the tube as an amplifier
can also be found from the graph of Fig. 11 or from the curves of Fig. 10.
Referring to Fig. 12, it can be seen that with fixed plate supply voltage,
Eb, the current flowing in the plate circuit will cause a voltage
drop across the load resistance, this drop being equal to IpR, where
Ip is the value of the plate current and R the resistance. The voltage
actually between plate and cathode of the tube is the plate-supply voltage minus
the voltage drop in the resistance. When an a.c. signal is applied to the grid,
the plate current varies at the same frequency, hence a corresponding a.c. voltage
is developed across the load resistor. This a.c, voltage is the useful output
of the tube. The maximum drop in the resistor occurs when the plate current
is maximum, corresponding to the most positive value of instantaneous grid voltage,
and the minimum drop occurs when the plate current is minimum, corresponding
to the most negative value of instantaneous grid voltage. In Fig. 11 these
plate-current values are 14.5 milliamperes for an instantaneous grid voltage
of -2.5, and 3.0 ma, for a grid voltage of -12.5. Since the plate load resistance
is 10,000 ohms, the maximum voltage drop is 0.0145 X 10,000, or 145 volts, and
the minimum drop is 0.003 X 10,000, or 30 volts. The difference, 145 - 30, or
115 volts, is the total change in voltage across the load corresponding to a
total change in grid voltage of 10 volts. Hence the voltage gain is 115/10,
or 11.5. The same information could be obtained from the curves of Fig. 10
by finding the currents corresponding to any chosen change in grid voltage,
and then proceeding as above to find the voltage output. From such information
a curve can be plotted showing the variation of amplification with load resistance.
EXPERIMENT 24
Class-A Amplification Apparatus:
The power supply, bias supply, v.t. voltmeter and tube board are used in this
experiment, together with a potentiometer or volume control and the resistors
specified in Exp. 23. Almost any potentiometer resistance may be used, although
values higher than about 100,000 ohms should be avoided if possible. The circuit
arrangement is shown in Fig. 13. The heater voltage for the tubes is used
as a source of a.c. voltage for the grid of the tube being tested, the value
of voltage applied to the grid being adjusted by means of the potentiometer.
The a.c. voltage in either the grid or plate circuit is measured by the vacuum
tube voltmeter, the input circuit of which is connected to the circuit being
measured through the 0.01-µfd. condenser. This condenser blocks the d.c. voltages
present and permits only the a.c, to be measured. Before performing the experiment
the v.t. voltmeter should be calibrated on a.c, A source of variable a.c, voltage
can most conveniently be obtained by making a slight change in the bias supply
so that its voltage divider can be connected directly across the a.c, line.
Referring to Fig. 2
page 56, July QST, disconnect the top end of R, from the filter and connect
it to the a.c. output terminal. Then proceed to calibrate the voltmeter by the
same method used in making the d.c, calibration, using the 0.01-µfd. blocking
condenser in the "hot" voltmeter lead. Connect the 1-µfd. condenser, C3,
to the cathode of the voltmeter tube (Fig. 6, page 66, August QST). The
calibration will be in terms of r.m.s. voltages, since the test set calibration
is r.m.s. The a.c, calibration will resemble that taken on d.c., except that
the curve above about 40 volts on the high range may show considerable departure
from linearity. If so, use only the linear part of this scale. This effect is
attributable to the fact that with a capacity of only 1 µfd. at C3
the time constant of the circuit is too small at 60 cycles to permit the cathode
bias to build up to a value sufficient to prevent grid current from flowing
at the higher applied voltages. In performing the experiment care should be
taken to keep the maximum voltage to be measured within the linear part of the
high-range curve.

Fig. 13 - Circuit arrangement illustration.
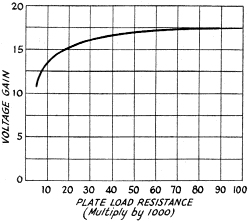
Fig. 14 - Voltage gain and plate load resistance data
plot.

Fig. 15 - Pentode characteristics apparatus experiment.

Table 1 - Plate load resistance in ohms and Output voltage
measurements.
Procedure: The purpose of this experiment is to confirm
by measurement the results of the gain calculations carried out as described
in Exp. 23. Adjust the grid bias (restore the voltage divider connection to
the filter after completing the a.c, calibration) and plate voltage to the values
used in the calculations, using the same tube. These were -7.5 and 300 volts
respectively in our example, using a 6J5. Set the potentiometer so that the
voltage applied to the grid is about 2 volts r.m.s. as measured between grid
and cathode (Fig. 13). Insert a resistor in the plate circuit of the tube
at R, and adjust the plate-supply voltage to the selected value (300 in this
illustration) with plate current flowing (push-button closed). Shift the v.t.v.m.
to the plate circuit and measure the a.c, output voltage, keeping the push-button
closed. Repeat for various values of plate load resistance, using two resistors
in series to make up values intermediate to those available in the single units.
The results of a typical
set of measurements are given below, for 2 volts r.m.s., applied to the grid
in Table 1.
The gain of the amplifier will be equal to the output voltage divided by the
input voltage, or just half (input voltage = 2) the figures above. Plot the
data in the form of a curve, as shown in Fig. 14.
Note that the gain rises 8B the plate load resistance is increased, but eventually
a point is reached where a considerable increase in load resistance causes only
a negligibly small increase in gain. The gain obtainable is proportional to
the amplification factor and also to the ratio of the plate load resistance
to the sum of the plate load resistance and the a.c, plate resistance of the
tube, and when the plate load resistance is large compared to the tube resistance
this ratio changes very slowly. Hence the amplification tends to level off as
the plate load resistance is increased. From the curves of Fig. 9 the
tube plate resistance is seen to be about
7500 ohms. When the plate load resistance is about 5 times the plate resistance,
or approximately 40,000 ohms, the amplification increases very slowly with further
increases in load resistance. Hence a load in the vicinity of 50,000 ohms is
a suitable value for this tube as a resistance-coupled voltage amplifier.
At 10,000 ohms, the value used in the illustration of Exp. 23, the measured
gain is about 13.5 as compared to the calculated value of 11.5. The percentage
difference, while fairly large, is to be expected in view of unavoidable errors
in measurement and in plotting and reading the curves. Also, the resistance
was assumed to be exactly 10,000 ohms in the calculations, while the manufacturing
tolerances on the resistors is 10%. Ohmmeter measurement of the resistor actually
used in the experiment showed the resistance to be on the high side of 10,000
ohms.
EXPERIMENT 2G
Pentode Characteristics
Apparatus: The apparatus set-up used in this experiment
is shown in Fig. 15. The power supply, bias supply, tube board and test
instrument are required. In taking one set of data it is necessary to maintain
the screen grid at constant voltage, preferably the rated value, and for this
purpose a VR-105-30 is substituted in the power supply for the VR-150-30 previously
specified. The tube tested can be a small receiving pentode such as the 6J7.
In making voltage measurements, the highest voltage range on the test instrument
which will permit reasonably accurate reading should be used so that the effects
of volt-age regulation will be minimized. The 500-volt scale for plate voltage
and 25-volt scale for grid voltage will be satisfactory (or nearest equivalent
ranges provided on the actual instrument).

Fig. 16 - 6K7 plate current and plate voltage data
curves.
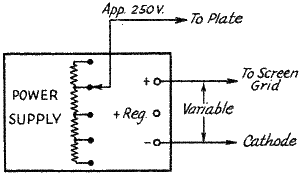
Fig. 17 - Connection of screen grid to the variable
tap on the power supply.
Procedure: In this experiment curves equivalent to those
plotted for the triode (Exp. 22) are to be obtained, for the purpose of determining
the relationships between plate current and grid and plate voltages in a pentode.
It is advisable to take data for the plate-voltage-plate current family first.
Using a 6J7, first set the grid bias at zero and then vary the plate voltage,
taking plate current readings at each value of plate voltage selected. From
a plate voltage of 100 up to the maximum available from the supply (about 400)
50-volt steps will be satisfactory, Below 100 volts it is suggested that readings
be taken at 10, 25, 50 and 75 volts. Each time the plate voltage is adjusted
be sure the push-button in the plate circuit is closed so that the voltage will
be set to the proper value with plate current flowing. When a set of measurements
has been made with zero grid bias, increase the bias to 1 volt negative and
repeat, Continue at 1-volt intervals in bias until a set of measurements has
been taken for -6 volts. At higher bias the plate current will be cut off, or
else so small in value as to be negligible. Plot the data in curves such as
are shown in Fig. 16. Comparing these curves to the equivalent triode
family in Fig. 7 shows a tremendous difference in the behavior of plate
current with varying plate voltage. In the triode case (Fig. 7) the plate
current is very markedly dependent upon the plate voltage. On the other hand,
except for the region of plate voltage lower than the screen voltage, the plate
current of the pentode is practically unaffected by the plate voltage. The curves
begin to droop as the plate voltage is reduced below 100, but the drop-off is
not really marked until the plate voltage is quite low. The fact that the plate
voltage has relatively little effect on plate current while the grid voltage
has a very great effect indicates that the amplification factor, ΔEp/ΔEg,
is very high.
The cause of this behavior is the screen grid. Since the
screen grid is an electrostatic shield, it prevents the electric field set up
by the plate from penetrating to the region occupied by the cathode and control
grid, hence electrons in this region are unaffected by the plate potential.
The control grid. however, has just as much effect on the electron stream as
it does in a triode. Electrons passing through through the control grid are
attracted to the screen because the latter is operated at a positive potential,
but many of them have sufficient velocity to pass between the screen-grid wires
without being caught by the screen grid itself. These electrons then come under
the influence of the electric field set up by the plate, and are attracted to
it, forming the plate current. Since the plate can attract only the electrons
which get through the screen, it is obvious that the plate current will be determined
almost wholly by the screen potential and the structure of the screen grid.
The effect of the screen grid on plate current can be found by holding the plate
voltage at a fixed value and varying the screen voltage (for a fixed value of
grid bias) while observing the plate current. A slight modification of the experimental
set-up of Fig. 15 is necessary. Connect the screen grid to the variable
tap on the power supply as shown in Fig. 17, and tap the plate connection
on the power-supply voltage divider so that the plate voltage will be about
250 volts. The first tap below maximum will be satisfactory. If the plate voltage
varies slightly during a run no harm will be done since the plate current is
only slightly affected by the plate voltage so long as it is appreciably higher
than the screen voltage. Vary the screen voltage in small enough steps so that
smooth, curves can be plotted from the data. Do this for several values of grid-bias
voltage. Typical experimental
curves obtained by this method are shown in Fig. 18, taken on a 6J7. These
curves have essentially the same nature as the curves of Fig. 7, which
is to be expected from the explanation of the operation of the screen-grid tube
given above.

Fig. 18 - 6J7 plate current and screen voltage curves.
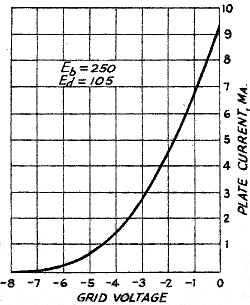
Fig. 19 - Plate current and screen voltage curve.

Fig. 20 - 6J7 oscillator test set-up.
Since the plate voltage has relatively little effect on the plate current,
a single-grid voltage-plate current curve will suffice for practically all plate
voltages above the screen voltage, so long as the latter is not changed. Such
a characteristic can be taken by holding the plate and screen voltages fixed,
reading plate current while varying the grid bias. An experimental curve on
a 6J7 is shown in Fig. 19. Although in the triode case the corresponding
curves (Fig. 6) had to be drawn for several values of plate voltage, in
this case such a series would lie so close together as to merge into one curve,
for all practical purposes. It can be seen, however, . that the curve has the
same general characteristics as those typical of triodes, and if the mutual
conductance is measured it will be found to be approximately the same as for
a triode of the same size. The plate resistance is obviously high, since a large
change in plate voltage is required to make a comparatively small change in
plate current. Both plate resistance and amplification factor are very difficult
to measure with any reasonable accuracy because in each case the ratio of the
two quantities involved is so high that the probable error in measuring the
smaller of the two re-flects a large error in the ratio.
Further experimental work may be done with the tube by plotting a series
of grid voltage-plate current curves for different values of screen voltage.
Also, the effect of secondary emission may be investigated by running a series
of plate voltage-plate current curves, corresponding to those of Fig. 16,
but with the suppressor grid connected to plate instead of cathode. The characteristics
of a variable-µ tube of the same general type, such as the 6K7, also may be
taken and compared to the sharp cut-off 6J7.
EXPERIMENT 26
Oscillator Operation Apparatus:
The power supply, v.t. voltmeter and tube board are needed for this experiment,
together with the additional parts indicated in the diagram of Fig. 20.
The Hartley oscillator circuit is indicated in this diagram, with parallel feed
in both plate and grid circuits. The radio-frequency chokes are 2.5-millihenry
pie-wound units, and the blocking capacities are midget mica condensers. Provision
should be made for changing the grid-leak resistance and for using different
values of load resistance. The 1-watt resistors used in previous experiments
will be satisfactory in both cases.
Procedure: The object of this experiment is to show the
effect of grid-leak resistance on oscillator plate current, grid current, and
r.f. output voltage, the plate voltage being fixed at some convenient value
and other circuit conditions left unchanged. In the circuit of Fig. 20
the tuned circuit is formed by one of the condensers and coils on the circuit
board, the whole 35-turn coil being used with the cathode of the oscillator
tube (a 6J5) tapped on the coil 10 turns from the grid end. The v t. voltmeter
is connected between the cathode and plate of the tube (through the plate blocking
condenser) to measure the r.f. plate voltage. The 1-µfd. by-pass condenser in
the v.t.v.m. cathode circuit (C3) should not be used.
With the plate voltage at some value which prevents excessive plate current,
such as 100 volts, insert a 5000-ohm resistor as a grid leak and measure the
plate current, grid current, and r.f. plate voltage. Adjust the plate voltage
to the chosen value with the plate circuit closed so that the tube draws plate
current. There should be no load on the oscillator on the first run. Change
the grid leak to 10,000 ohms and repeat, then continue with successively higher
values of grid-leak resistance up to 100,000 ohms. Connect a 25,000-ohm resistor
across the v.t.v.m. input circuit as a load and repeat the measurements. Continue
with lower values of load resistance until the circuit refuses to oscillate.
The data may then be plotted in graphical form.
Typical results of such measurements are shown in the curves of Fig. 21.
Curves for no load and for a load of 10,000 ohms are shown for comparison, although
if several values of load resistance are used it would be better to use separate
sheets for each, to avoid confusion. With no load the variation in r.f. output
voltage over the whole range of grid-leak resistance is relatively small. The
plate current is low and decreases somewhat as the grid-leak resistance is increased.
The grid current at the lowest grid-leak resistance is relatively high, but
decreases with increasing grid-leak resistance. The grid bias - product of grid
current by grid-leak resistance - shows comparatively little variation, indicating
the self-regulating properties of the oscillator in this respect; that is "the
grid current regulates itself so as to develop about the same bias over a wide
range of grid resistance,

Fig. 21 - Plate current and output voltage for values
of grid leakage.
When the circuit is loaded the plate current shows a pronounced increase.
This is partly because the load reduces the Q of the tuned circuit, thus lowering
its parallel impedance and hence allowing more plate current to flow, much in
the same way that the plate current increased in the curves of Fig. 10
with lower load resistance for a fixed value of grid bias. At the same time
the r.f. output voltage decreases while the internal voltage drop in the tube
increases. This effect is comparable to the decrease in amplification with lower
load resistance which was observed in Exp. 24. The plate-current increase is
exaggerated in the case of the oscillator because the decrease in r.f. plate
voltage is accompanied by a proportional decrease in r.f. grid voltage, since
the r.f, grid voltage is obtained from the plate circuit. Hence the grid bias
also decreases, if the grid-leak resistance and feed-back coupling are fixed.
With lower grid bias more plate current will flow, and to some extent the amplification
increases so that the r.f. output voltage tends to become greater. Thus two
tendencies working in opposite directions are- present, but with the net result
that there is a decrease in both r.f. output voltage and grid bias and an increase
in plate current. Increasing the value of grid-leak resistance again results
in self-regulating action with respect to grid bias, while r.f. output voltage
and plate current decrease together.
The experiment can be extended by making a similar set of observations with
a new value of feed-back, obtained by changing the position of the cathode tap
on the coil. It is also of interest to compare the operation of the various
oscillator circuits which can be made up from the coils and condensers on the
circuit board.
ANSWERS TO PROBLEMS IN INSTALLMENT 3 If no answer is
given to a question, it is to be found in the appropriate Handbook section or
in the description of the experiment or experiments accompanying that section.
Assignment 8: Q.2 - 10 volts; 500 volts; 500 volts.
Q.6 - 125; 55,000 ohms.
Q.7 - Neglecting internal resistance: 11.4; 39.6 ohms. Including internal
resistance: 10.4; 38.7 ohms.
Q.9-4.55 µh.; 114 µµfd.
Q.10 - The curve should go through the following points:
50 µµfd. - 41.4 µh.
100 µµfd. - 20.7 µh.
150 µµfd. - 13.8 µh.
200 µµfd. - 10.4 µh.
250 µµfd. - 8.3 µh.
Q.11 - The curves should go through the following points:

Q.12 - 3760 kc.
Q.13 - a) 7120 kc.
b) 224. c) 100,000
ohms. d) 224 volts.
e) 1.12 volts; 0.56 amp.; 0.0025 amp.; 224 - Q.
f) 7400 ohms; error = 8.1 % (could be neglected); 160%.
g) Neglecting internal resistance: 0.56 amp.; 0.0312 amp.; 17.9.
Including internal resistance: 0.557 amp.; 0.0338 amp.; 16.5.
Q.14 - 2.99 µh.; 42 µµfd.
Q.18 - Same in both cases.
Q.19 -10 ohms.
Q.20 - 63.3 µµfd.; 157,000 ohms.
Assignment 9: Q.7 - 135 µh.; 3.7 µµfd.; no; 1.35
µh.; 370 µµfd.; tap load down on coil.
 Q.8 - (For a frequency
of 7120 kc.): Q.8 - (For a frequency
of 7120 kc.):
Capacity values for circuit A are maximum, for circuit B minimum; fairly
wide range of values can be used with circuit C.
Assignment 10:
Q.2 - 85.7 meters; 281 feet.
Q.9-450 kc., 4450 kc.; 3901.5 kc., 3898.5 kc.; 1000 cycles, 14,299 kc.
Q.14 - 19 µµfd. or higher.
Q.15 - 32 µfd. or higher.
Q.16 - 1.1 millihenry or higher.
Q. 17 - Yes (47,000 ohms); no (5650 ohms).
Related Pages on RF Cafe - Tube
Base Diagrams - A Course in
Radio Fundamentals-Vacuum Tubes Sep 1942 QST -
Electrons on Parade
Tube Production Video by RCA c.1942 -
NEETS Module 6 - Vacuum Tubes
- Vacuum Tube Vendors
Posted February 1, 2021
(updated from original post on 2/21/2011)
|






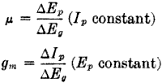

























 Q.8 - (For a frequency
of 7120 kc.):
Q.8 - (For a frequency
of 7120 kc.): 


