After Class: Speaking of Magnetism - Part 1, August 1958 Popular Electronics

For some reason, a lot of people seem to have a harder time grasping the concepts of magnetism than the concepts of electricity. Maybe it is because most of the machines and appliances we are familiar with run off of electricity supplied by the electric utility distribution system - not the magnetism distribution system. The fact that motors, transformers, and relays, which are present in one form or another in every household, office, and factory, are as reliant upon magnetic effects as they are electrical effects is lost on the multitudes. Maybe if we received monthly magnet bills to pay instead of electric bills, there might be more interest in understanding the phenomenon. At the most fundamental level, electric and magnetic circuit equations exist that are nearly the same, but with magnetism terms used rather than electricity terms; i.e., duality. This "Speaking of Magnetism" article in the monthly "After Class" section of the August 1958 issue of Popular Electronics magazine provides an introduction to the topic of magnetism.

The expression "like poles repel and unlike poles attract," repeated often enough, tends to give a theoretical concept a reality it does not possess. You wouldn't think of using a screwdriver to tighten a hex nut just because it works so well on a slotted head. Similarly, the magnetic pole concept - good as it may be for explaining fundamental interactions between permanent magnets - fails miserably when you try to apply it to more complex magnetic phenomena.

The question is: can we do away with magnetic poles altogether? Yes, we can if we wish, but we do not have to go to this extreme. If we think of poles and their interactions merely as "rules of thumb" and use them properly, they can serve as helpful tools. But when we consider basic explanations, let's work exclusively with magnetic fields and lines of force.

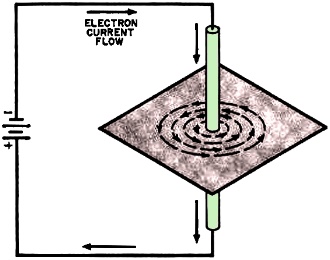
Fig. 1 - The magnetic effect of a current passing down through a vertical wire. Iron filings sprinkled on cardboard sheet trace out the magnetic forces.

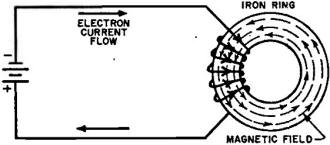
Fig. 2 - The magnetism in a toroid or closed-ring solenoid.

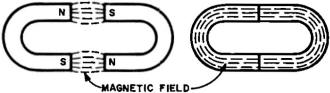
Fig. 3 - Magnetic poles seem to vanish when two U-magnets are brought together this way.

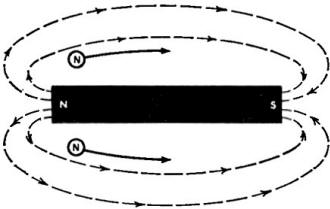
Fig. 4 - Field direction is arbitrarily taken as the direction over which an isolated little N-pole would travel if it were permitted to do so.

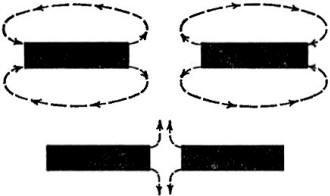
Fig. 5 - Magnetic lines of force behave as if there were a force of mutual repulsion between them; and they act as if they were under tension, fending to contract to the smallest possible length.

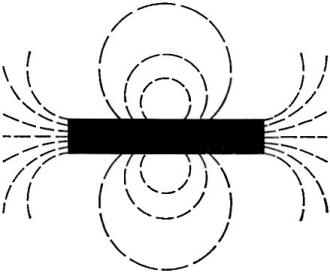
Fig. 6 - When adjacent lines have the same direction, there is a force of repulsion between them that causes repulsion between their parent magnets.

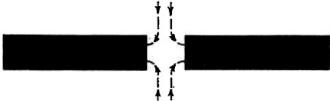
Fig. 7 - The same effect is shown here as in Fig. 6 except that both sets of lines have been reversed in direction by turning them end over end.

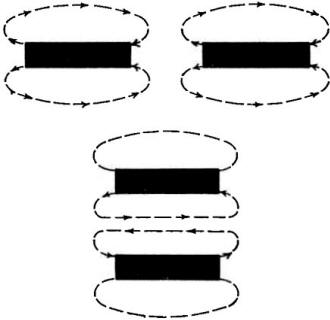
Fig. 8 - Two conditions that result in attraction between magnets. In both cases, the directions of the magnetic lines of force are opposed.

For example, when an electron current flows through a vertical conductor passing through a sheet of cardboard (Fig. 1), iron filings sprinkled on the cardboard form concentric rings around the wire. This magnetism is just as "real" as the magnetism around a bar magnet. Yet, where are the poles?

Or consider a ring of iron magnetized by a coil through which an electron current flows (Fig. 2). A strong magnetic field exists inside the iron core but, again, where are the poles? There just aren't any!

Figure 3 illustrates another good example of the same kind of thing. Two U-magnets separated by a reasonable distance are generally conceded to be polarized individually. Each one has its own N-pole and its own S-pole.

With opposite poles facing each other, we push them together to form a closed ring. If the pole faces are very smooth so that really intimate contact can be established, polar identity completely vanishes and the magnetic field is entirely confined within the metal.

Fundamental Definitions. To help you follow the line of reasoning we are going to develop, and to make possible exact descriptions of magnetic phenomena in terms of fields rather than poles, we will need a few fundamental definitions.

This is a condition of space surrounding a magnet in which magnetic effects can be detected. The shifting of an iron filing when placed near a magnet indicates that the filing is being acted upon by the magnetic field.

Lines of Force. It is convenient to think of magnetic fields as being composed of individual lines of force. Lines of force as such have no real existence; they simply serve as descriptive aids.

The lines of force comprising a field are not in motion if the source of the field is at rest. Yet, because a magnetic compass will always point in a given direction when placed in a field, we arbitrarily define field direction as the path that an isolated N-pole follows under the influence of the magnetic forces. (Notice that we have not completely abandoned the idea of poles since we use an N-pole to establish our arbitrary field direction. When we speak of an N-pole in this sense, we refer to that end of a magnetic compass which points in a northerly direction when it is free to turn.)

N-pole and S-pole. If we have to bring poles into our discussion at all, we should define them exactly. From the description of the direction of a field just given, we can safely define an N-pole as that end of a magnet from which the lines of force emerge into the air; in contrast, an S-pole is then the end into which the lines of force re-enter the magnet. (See Fig. 4.) Such a definition is perfectly consistent with the arbitrarily selected field direction based upon the path of an isolated N-pole under magnetic influence.

The notion of magnetic lines of force is due to the work of Michael Faraday (1791-1867). He thought of these lines as if they were real, and used them to interpret magnetic phenomena. Following his lead, we can see that these lines have some very definite properties.

2. Lines having the same arbitrary direction and lying adjacent to each other repel each other.

3. Lines of force are under tension and, like stretched rubber bands, tend to contract to the shortest possible length.

If these oppositely directed lines originate in two different magnetic bodies, the mutual attraction of the lines results in a mutual attraction of the bodies.

Figure 5 illustrates the first three of these properties. Lines "emerging" from the N-pole begin to spread apart by repulsion as soon as they appear in the air, and there is no tendency for one line to cross any other. The curved lines above and below the magnet resemble inflated balloons seen in cross-section in that they appear to want to contract back into the magnet but cannot do so due to the mutual repulsion between them.

These properties explain simple interactions without any reference to poles at all. First examine the sequence in Fig. 6.

Two magnets separated by a substantial distance are placed so that the lines of force emerge from the two ends closest to each other; these lines follow independent patterns as though they were alone in space. As they are brought close to each other, it is evident that lines having the same direction will be adjacent and that repulsion will take place, not only between the lines of force, but also between the magnets themselves.

Exactly the same effect occurs when we bring the other two poles close to one another as in Fig. 7. Thus, we are not saying that "like poles repel" but we are attributing the interaction to something that occurs in the space between the magnets rather than in the ends of the magnets themselves. This is a fine but important distinction, as you will see.

A second possible condition, as in Fig. 8, is the one in which two magnets are positioned so that oppositely directed lines of force lie adjacent, either with the magnets end-to-end or side-by-side. The fourth property of lines of force tells us that attraction between magnetic lines, and hence attraction between the magnetic bodies, should occur. This explains why "opposite poles attract" without the need for referring to poles at all.

Attraction and Repulsion. You might reasonably comment at this point that nothing we have described by lines of force could not also have been adequately described using the pole concept. In a sense, you would be perfectly right, because the attraction and repulsion of poles is a usable tool in working with these simple and fundamental interactions.

However, we have shown that there are no poles in the magnetic field of a single current-carrying wire (Fig. 1) or in a closed-ring solenoid. Yet, if we place two parallel wires near each other, there will be definite attractions and repulsions depending upon the direction of the currents through them.

If there are no locatable poles, how will you predict the directions of the forces? Again, two pole-less ring solenoids adjacent to one another will also show the presence of magnetic forces. Without specifying pole position, can you predict the attraction or repulsion?

In next month's After Class, we will demonstrate how magnetic fields can be used to describe all interactions, regardless of poles or the absence of poles. As a matter of fact, we will include one phenomenon that forces you to arrive at the wrong conclusion if you use the pole concept but leads you directly to the correct answer if you employ the field idea.

After Class: Speaking of Magnetism - Part 1 August 1958 Popular Electronics

After Class: Speaking of Magnetism - Part 1
August 1958 Popular Electronics