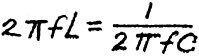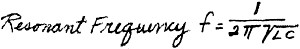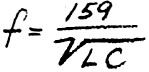May 1961 Popular Electronics
 Table of Contents Table of Contents
Wax nostalgic about and learn from the history of early electronics. See articles
from
Popular Electronics,
published October 1954 - April 1985. All copyrights are hereby acknowledged.
|
Fundamentals of resonant
tank circuits has not changed since they were first investigated more than a century
ago. This "After Class" tutorial that ran in the May 1961 edition of Popular Electronics
is typical of the series where the author speaks as though he was giving an impromptu
lesson to a gathering of students after the scheduled classroom period was over
or, in this instance as though he was having a casual discussion with a friend who
was perplexed by a particular electronics phenomenon. Figures and equations are
often drawn by hand to augment the informal setting rather than being typeset. Here,
"Larry" is amazed by the great performance of his Ham radio with its ability to
filter out adjacent channel interference. Mentor "Ken" takes the opportunity to
explain the mathematics and physics of resonant circuits both to tuning antennas
and for filtering unwanted frequencies while passing desired frequencies.
After Class: Explaining Tuned Circuits
By Saunder Harris, WINXL
Coil and capacitor combinations lie behind every tuned circuit, and some do a
better job than others. Here's the complete story of how they work and why.
Larry was busy listening to the chatter of the 40-meter band on Ken's receiver.
An old hand on the air, Ken watched as his young friend delicately turned the bands
pre ad dial.
"Smooth-operating gadget, isn't it, Larry?"
"You said it, Ken. Boy, the way this thing separates signals is amazing. Listening
to 40 meters on my receiver is like trying to count the noodles while the soup is
being stirred. With this one, not only can you count the noodles, but you can pick
the particular noodle you want out of the soup at any time."
"You're always thinking about eating." Ken shook his head. "Well, Larry, you
can thank the tuned circuits in this baby for separating signals. As a matter of
fact, if it weren't for tuned circuits, you and I would be collecting stamps for
a hobby instead of guiding electrons through wires. There wouldn't be any radio
... or TV for that matter. Some horrible thought, eh ?"
"Now that you've mentioned it, Ken, I've always wondered how receivers separate
one frequency from another - especially two frequencies almost on top of each other."
Larry flipped off the receiver and sat back. "Can you make with some explaining
on the topic, friend?"
"Since you put it so nicely, I'll be glad to. As usual, we'll start off with
some basic facts."
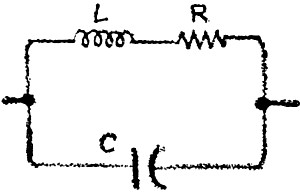
Ken took up paper and pencil as he said, "Tuned circuits in receivers are combinations
of inductance, capacitance, and resistance. These three elements are usually arranged
in a two-leg parallel circuit, like this." He passed the drawing he had made over
to Larry.
Larry studied the drawing for a moment. "So receiver tuned circuits are made
up of coils, capacitors, and resistors ?"
"Not exactly, Larry. Actually," Ken explained, "the resistance is not deliberately
added. It pops up in the circuit because the wire making up the coil, L, and the
connecting leads and solder joints all insert some resistance into the tuned circuit.
We try to avoid unintentional resistance by keeping leads short and making good
solder connections."
"I'm with you so far, but I still don't see how receiver tuned circuits work.
What happens when I turn the tuning knob of a receiver?"
"Let's not get ahead of ourselves, Larry." Ken paused a moment. "Now, one of
the things that makes a tuned circuit possible is the fact that both a coil and
a capacitor oppose the flow of alternating current through them. This opposition
to current flow can be considered as resistance, but in a.c. circuits it's called
reactance.
"As you increase the frequency of an alternating current passing through a capacitor,
it becomes easier for that current to get through - in other words, the capacitive
reactance decreases. For the coil, however, the higher the frequency, the rougher
it is for the current to get through - the inductive reactance increases as the
frequency rises."
Ken paused again to see if everything he had said so far was understood. At a
nod from Larry, he went on.
"The second thing that makes tuned circuits possible is that, unlike pure resistance,
both capacitive and inductive reactances have directional properties. Take a look
at that parallel-tuned circuit I showed you and imagine an alternating current flowing
through it.
"Each element in the circuit will have a current flowing through it, the amount
of current depending on the reactance of the circuit component. The thing to keep
in mind, though, is that the current through the coil will always be opposite in
'polarity' to the current through the capacitor ... "
At this point, Larry yelled, "Whoa up! I'm beginning to get lost!"
 "Relax, the hard part's over now." Ken took
a ruler from the workbench and handed it to Larry. "Here, let's see you balance
this on your finger." "Relax, the hard part's over now." Ken took
a ruler from the workbench and handed it to Larry. "Here, let's see you balance
this on your finger."
Larry took it, looking puzzled. "What has balancing a ruler got to do with tuned
circuits?" He shrugged, "Okay, so I've got it balanced. What happens now?"
"A tuned circuit is very similar to the situation you have with the ruler balanced
on your finger. Can you imagine how you might get a similar electrical balance in
this parallel-tuned circuit?"
Larry frowned; then a big grin suddenly appeared on his face. "Wait a minute!
Suppose I put a voltage of a certain frequency across the circuit. Let's say that
at that frequency the capacitive reactance is greater than the inductive reactance
... "
Ken nodded encouragingly.
"As I raise the frequency, the capaci-tive reactance gets smaller and the in-ductive
reactance gets larger ... "
"Right, Larry! Go on."
"If I keep raising the frequency, I'll eventually reach a point where the capacitive
reactance and the inductive reactance are equal. This part is easy, but what happens
inside the parallel-tuned circuit when we have this electrical balance?"
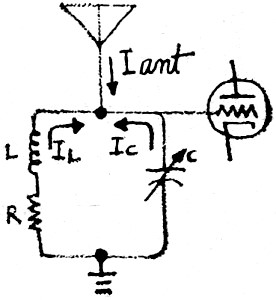
"The frequency at which the capacitive and inductive reactances are equal is
called the resonant frequency. To see what happens inside the parallel-tuned circuit
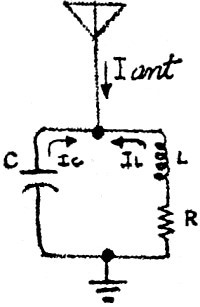
at resonance, look at this diagram, Larry."
"Do you recall Kirchhoff's law about currents that enter and leave any point
in a circuit adding up to zero? Well, at resonance, since the inductive and capacitive
reactances are equal, the currents in L and C are also equal but opposite in phase;
so they add up to zero. Now, if IL and IC add up to zero at
resonance, what is the value for Iant?"
Larry began to think aloud. "Let's see ... the three currents have to add up
to zero. That means IC plus IL plus Iant equals
zero. But at resonance, IC and IL add up to zero, so that
leaves only v to equal zero ... hey, the current from the antenna is zero!"
"Right you are, Larry." Ken sounded pleased. "But let's put that mental solution
of yours down on paper to be sure we have it cold."
"Say, Ken," Larry asked, "if the antenna can't pass any current through the parallel-tuned
circuit at the resonant frequency, then the tuned circuit behaves exactly like an
open circuit. Is that correct?"
"Sure thing - so far you're batting a thousand. Now let's draw the schematic
diagram of a receiver front end, and come to some conclusions." In a moment the
sketch was done.
Ken continued with his explanation. "First off, let's see what happens at the
resonant frequency. The tuned circuit behaves like a very high impedance or high-value
grid resistor at this frequency, and very little of the signal picked up by the
antenna passes to ground through the tuned circuit. Instead, the control grid of
the vacuum-tube stage connected to the top of the tuned circuit sees nearly all
of this signal and amplifies it.
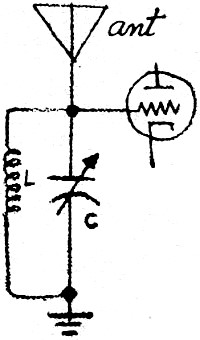 "Other signals picked up by the antenna which
are lower than the resonant frequency do not meet with this high impedance. They
are bypassed to ground through the coil, L, which offers very little impedance.
Hence, the control grid sees no signal developed across the tuned circuit. True,
there is some signal, but it is probably smaller than the noise generated in the
tube and will not be amplified. Signals higher than the resonant frequency are bypassed
to ground because the capacitor, C, offers very little impedance, and again the
control grid receives no useful signal." "Other signals picked up by the antenna which
are lower than the resonant frequency do not meet with this high impedance. They
are bypassed to ground through the coil, L, which offers very little impedance.
Hence, the control grid sees no signal developed across the tuned circuit. True,
there is some signal, but it is probably smaller than the noise generated in the
tube and will not be amplified. Signals higher than the resonant frequency are bypassed
to ground because the capacitor, C, offers very little impedance, and again the
control grid receives no useful signal."
"Fine, Ken, I think I'm beginning to understand. But I noticed that you made
the capacitor in the diagram a variable job ... "
"And with good reason," Ken shot back. "Think a moment. If we use fixed values
for Land C, only one frequency will resonate across this circuit. And ... "
Larry didn't let him finish, but broke in, saying, "Oh, I see! If we couldn't
vary the C, we could only listen to one frequency; and if no station were transmitting
on this frequency, we wouldn't hear anything."
"Right again. So we use a variable capacitor and vary the value of C so we can
pick out the frequency at which we want to resonate the tuned circuit. This way,
we pick the station we want - not let the station find us."
"I get you," said Larry. "Now where do we go from here?"
Well, now that we've tackled tuned circuits in words, I'd like to show you how
they work out in terms of equations for reactances and resonance. That's the best
way to see what's going on."
Larry winced, and Ken laughed at the uncomfortable look on his young friend's
face. "You might as well get the equations down for figuring resonant frequencies,"
he said. "They're handy to know, and you'll need them if you take the General Class
ham exam. I guarantee they're easy to understand."
Ken did some writing, then pushed the paper over so Larry could read it.
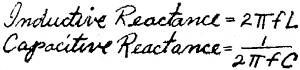 "I'll bet I can figure out how we find the resonant
frequency for a tuned circuit from those two equations. This isn't bad after all,"
Larry admitted. "I'll bet I can figure out how we find the resonant
frequency for a tuned circuit from those two equations. This isn't bad after all,"
Larry admitted.
"Go to it, and good luck," said Ken. "Well, I guess the ƒ in the formulas
stands for the frequency, the C for capacitance in farads, and the L for inductance
in henrys."
"Okay. And ... ?"
"A few minutes ago you mentioned that at the resonant frequency the capacitive
and the inductive reactances are equal. So, if we set each of the reactance formulas
equal to each other, and do a little fancy algebra work, we should get one formula
for the frequency, ƒ, in terms of L and C."
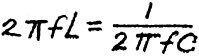
"Nice going, Larry - that's 100% correct." Ken was really pleased. "I'll save
you some brainwork and show you how it works out." He took the scratch paper from
Larry and wrote:
"Now I solve for ƒ by simple algebra and come up with an equation worth
re-membering." Ken wrote down:
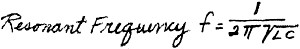
"In this equation, Larry, you must remember that the frequency comes out in cycles
per second. The capacity must be expressed in farads and the inductance in henrys.
You'll get all fouled up if you use the wrong units. Pi (π) is just your old
friend from geometry, 3.14."
"Isn't there any formula in micro-farads and microhenrys we can use, Ken? Changing
all the units around could make an awful mess."
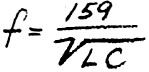
"I'm glad you asked that, Larry. There sure is. Here, let me write it out for
you."
"This formula is real easy to use," said Ken, passing the paper to Larry. "The
capacitance units you substitute for Care micromicrofarads (μμƒ.); the
inductance units you substitute for L are expressed in microhenrys (μh.). These
are the values you'll most likely use in practical work. Your answer then comes
out in megacycles."
"It's all clear now," observed Larry, as he finished studying the equations.
"Say, before we call it a night, Ken, would you do me a favor and explain what
they mean by the Q of a tuned circuit ?"
"I sure will; Q is an important part of any discussion of tuned circuits and
we shouldn't forget to clear up any doubt as to what it means. Do you remember what
you said about the sharp tuning of my receiver a while back?"
"Do I!" replied Larry. "It was terrific."
"It was the Q of the circuit that made it that way. But I cheated before, Larry,"
Ken admitted. "I drew the front end of a receiver showing the tuned circuit without
the resistance. Let's draw it again, and patch up our thinking. At the same time,
you'll get a clear understanding of exactly what Q is." He began to sketch quickly.
 "Before," Ken continued, "we said that at
the resonant frequency the currents IC and IL added up to
zero. This just ain't so. The resistor, R, causes a phase shift in the coil leg
of the tuned circuit. Since this resistance is small, the phase difference between
the currents IC and IL is slightly less than 180 degrees,
and summing up these two currents will not give us zero. A very small current will
be left. Back to friend Kirchhoff ..."
Again Larry interrupted, "I get it!
The sum of the currents entering and leaving anyone point in a circuit must be
zero - so since the sum of IC and IL is a very small current,
a current of equal size but opposite phase must be supplied to the tuned circuit
by the antenna."
"Atta boy, Larry," said Ken beaming.
"Antenna current flows in spite of the fact that the circuit is at resonance.
The tuned circuit, instead of being an open circuit, now exhibits some high resistance.
This will always be the case since we can never get rid of the resistance in the
coil or at soldered connections. But we can keep the resistance down to some low
value where it won't bother us."
"Why?" Larry asked.
"The more resistance in the circuit, the less selective the circuit. That's why
your receiver has trouble separating close stations and mine doesn't. Mine is more
selective.
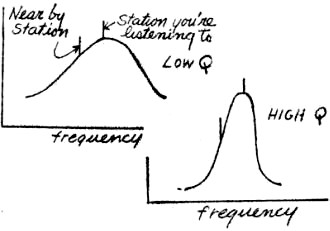 "We can say the same thing in a different way," Ken pointed out.
"The more resistance in a tuned circuit, the lower its Q. The Q of a circuit is
a numerical way of expressing the merit of a tuned circuit. Look at these curves.
The top one shows a low-Q tuned circuit in operation. You can see how broad the
curve is. If you tune the receiver correctly, the station you want to listen to
will be right on top of the curve. But note that a nearby station, which you don't
want to hear, will have almost the same signal strength - the tuned circuit will
not reject it. This shows poor selectivity." Pointing to the top drawing, Ken added,
"That's your receiver!" "We can say the same thing in a different way," Ken pointed out.
"The more resistance in a tuned circuit, the lower its Q. The Q of a circuit is
a numerical way of expressing the merit of a tuned circuit. Look at these curves.
The top one shows a low-Q tuned circuit in operation. You can see how broad the
curve is. If you tune the receiver correctly, the station you want to listen to
will be right on top of the curve. But note that a nearby station, which you don't
want to hear, will have almost the same signal strength - the tuned circuit will
not reject it. This shows poor selectivity." Pointing to the top drawing, Ken added,
"That's your receiver!"
"I see yours right below it," Larry said. "The curve is more peaked, so the tuning
is sharper. Also, the nearby station is almost rejected. In fact, I bet it won't
be heard at all."
"You get the point, Larry. So the Q is only a means of expressing the quality
of the tuned circuit. To compute it, you divide the inductive reactance by the resistance
in the circuit.
"You can see that the less resistance, the higher the Q; and the higher the Q,
the more selective the circuit. When you're building a set, you should be care-ful
to keep leads as short as possible, make good solder joints, and do everything possible
to keep the resistance down and the Q up."
"I guess that's a lesson I'll remember the next time I heat up the old soldering
iron." Larry tried to hide a yawn.
"If that's a hint you've had enough, I can take it, buddy." Ken laughed as he
got up. "Let's call it a session. But before you run off, let me remind you to go
over what we've talked about. You took such a big bite of theory, you'd better chew
on it a while."
Posted August 27, 2020
(updated from original post on 4/16/2014)
"After Class" Topics
|





 "Relax, the hard part's over now." Ken took
a ruler from the workbench and handed it to Larry. "Here, let's see you balance
this on your finger."
"Relax, the hard part's over now." Ken took
a ruler from the workbench and handed it to Larry. "Here, let's see you balance
this on your finger." 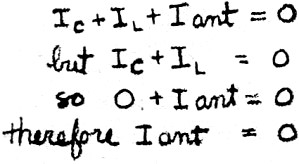
 "Other signals picked up by the antenna which
are lower than the resonant frequency do not meet with this high impedance. They
are bypassed to ground through the coil, L, which offers very little impedance.
Hence, the control grid sees no signal developed across the tuned circuit. True,
there is some signal, but it is probably smaller than the noise generated in the
tube and will not be amplified. Signals higher than the resonant frequency are bypassed
to ground because the capacitor, C, offers very little impedance, and again the
control grid receives no useful signal."
"Other signals picked up by the antenna which
are lower than the resonant frequency do not meet with this high impedance. They
are bypassed to ground through the coil, L, which offers very little impedance.
Hence, the control grid sees no signal developed across the tuned circuit. True,
there is some signal, but it is probably smaller than the noise generated in the
tube and will not be amplified. Signals higher than the resonant frequency are bypassed
to ground because the capacitor, C, offers very little impedance, and again the
control grid receives no useful signal." 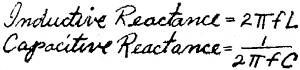 "I'll bet I can figure out how we find the resonant
frequency for a tuned circuit from those two equations. This isn't bad after all,"
Larry admitted.
"I'll bet I can figure out how we find the resonant
frequency for a tuned circuit from those two equations. This isn't bad after all,"
Larry admitted.