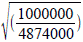The exact theory of Fresnel (pronounced "Fray-nell") zones is quite complicated.
However, the concept is quite easy to understand: we know from the Huygens principle
that at each point of a wavefront new circular waves start, we know that microwave
beams widen as they leave the antenna, we know that waves of one frequency can interfere
with each other. Fresnel zone theory simply looks at a line from A to B, and then
at the space around that line that contributes to what is arriving at point B. Some
waves travel directly from A to B, while others travel on paths off axis and reach
the receiver by reflection.
Consequently, their path is longer, introducing a phase shift between the direct
and indirect beam.
Wireless Networking in the Developing
World
Many thanks to the authors for making this very informative works available per
the Creative Commons ShareAlike license.
"The overall goal of this book is to help you build affordable communication
technology in your local community by making best use of whatever resources are
available." - The Authors
Some pertinent parts of the book are excerpted here. To access the complete document,
please visit https://wndw.net.
Whenever the phase
shift is one half wavelength, you get destructive interference: the signals cancel.
Taking this approach you find that when the reflected path is less than half
a wavelength longer than the direct path, the reflections will add to the received
signal. Conversely, when the reflected path length exceeds the direct path by more
than one half wavelength, its contribution will decrease the received power. Figure
RP 11: The Fresnel zone is partially blocked on this link, although the visual line
of sight appears clear.
Note that there are many possible Fresnel zones, but we are chiefly concerned
with the first zone, because the contributions from the second zone are negative.
The contributions from the third zone are positive again, but there is no practical
way to take advantage of those without the penalty incurred in going through the
second Fresnel Zone.
If the first Fresnel zone is partially blocked by an obstruction, e.g. a tree
or a building, the signal arriving at the far end would be diminished. When building
wireless links, we therefore need to be sure that the first zone is kept free of
obstructions. In practice, it is not strictly necessary that the whole of this zone
is clear, in wireless networking we aim to clear about 60 percent of the radius
of the first Fresnel zone.
Here is one formula for calculating the radius of the first Fresnel zone:
r = 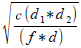
...where r is the radius of the zone in meters, d1 and d2 are distances from
the obstacle to the link end points in meters, d is the total link distance in meters,
and f is the frequency in MHz.
The first Fresnel zone radius can also be calculated directly from the wavelength
as:
r =  with all the variables
in meters
with all the variables
in meters
It is apparent that the maximum value of the first Fresnel zone happens exactly
in the middle of the trajectory and its value can be found setting d1=d2=d/2 in
the preceding formulas. Note that the formulae give you the radius of the zone,
not the height above ground.
To calculate the height above ground, you need to subtract the result from a
line drawn directly between the tops of the two towers.
For example, let's calculate the size of the first Fresnel zone in the middle
of a 2 km link, transmitting at 2.437 GHz (802.11b channel 6):
r = 17.31
r = 17.31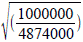
r = 7.84 meters
Assuming both of our towers were ten meters tall, the first Fresnel zone would
pass just 2.16 meters above ground level in the middle of the link. But how tall
could a structure at that point be to block no more than 60% of the first zone?
r = 0.6 * 7.84 meters
r = 4.70 meters
Subtracting the result from 10 meters, we can see that a structure 5.3 meters
tall at the center of the link would block up to 40% of the first Fresnel zone.
This is normally acceptable, but to improve the situation we would need to position
our antennas higher up, or change the direction of the link to avoid the obstacle.






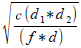
 with all the variables
in meters
with all the variables
in meters