Module 11 - Microwave Principles Pages
i,
1-1, 1-11,
1-21,
1-31,
1-41,
1-51,
1-61,
2-1,
2-11, 2-21,
2-31,
2-41,
2-51,
2-61,
3-1,
3-11,
AI-1,
Index-1,
Assignment 1,
Assignment 2
Chapter 2
Microwave COMPONENTS and Circuits Learning
Objectives Upon completion of this chapter the student will be able to: 1. Explain the
basic principles of microwave tubes and describe the limitations of conventional tubes. 2. Describe the
basic principles of velocity modulation. 3. Outline the development of microwave tubes. 4.
Describe the basic theory of operation of klystrons including multicavity and reflex klystrons. 5. Explain
the basic theory of operation of traveling-wave tubes and backward-wave oscillators. 6. Describe the
construction, basic theories of operation, and typical applications of magnetrons and amplitrons. 7.
Describe the basic theory of operation of tunnel diodes when used in oscillator-, amplifier-, and
frequency-converter circuits. 8. Explain the operation of varactors when used in parametric amplifiers and
frequency converters. 9. State the basic principles of operation of bulk-effect diodes and the Gunn
oscillator. 10. Explain the basic operation of passive microwave diodes in terms of theory and
application. 11. Explain the basic operation of microwave transistors in terms of theory and application.
Microwave COMPONENTS The waveguides discussed in chapter 1 serve to transport microwave energy from
one place to another. Energy is transported after it has been generated or amplified in a previous stage of the
circuit. In this chapter you will be introduced to the special components used in those circuits. Microwave energy is used in both radar and communications applications. The fact that the frequencies are very
high and the wavelengths very short presents special problems in circuit design. Components that were previously
satisfactory for signal generation and amplification use are no longer useful in the microwave region. The theory
of operation for these components is discussed in this chapter. Because the theory of operation is sometimes
difficult to understand, you need to pay particular attention to detail as you study this chapter. It is written
in the simplest manner possible while retaining the necessary technical complexity. 2-1
Microwave TUBE Principles The efficiency of conventional tubes is largely
independent of frequency up to a certain limit. When frequency increases beyond that limit, several factors
combine to rapidly decrease tube efficiency. Tubes that are efficient in the microwave range usually operate on
the theory of VELOCITY MODULATION, a concept that avoids the problems encountered in conventional tubes. Velocity
modulation is more easily understood if the factors that limit the frequency range of a conventional tube are
thoroughly understood. Therefore, the frequency limitations of conventional tubes will be discussed before the
concepts and applications of velocity modulation are explained. You may want to review NEETS, Module 6,
Introduction to Electronic Emission, Tubes, and Power Supplies, Chapters 1 and 2, for a refresher on vacuum tubes
before proceeding. Frequency Limitations of Conventional Tubes Three
characteristics of ordinary vacuum tubes become increasingly important as frequency rises. These characteristics
are interelectrode capacitance, lead inductance, and electron transit time. The Interelectrode
CapacitanceS in a vacuum tube, at low or medium radio frequencies, produce capacitive reactances that are so large
that no serious effects upon tube operation are noticeable. However, as the frequency increases, the reactances
become small enough to materially affect the performance of a circuit. For example, in figure 2-1A, a 1-picofarad
capacitor has a reactance of 159,000 ohms at 1 megahertz. If this capacitor was the interelectrode capacitance
between the grid and plate of a tube, and the RF voltage between these electrodes was 500 volts, then 3.15
milliamperes of current would flow through the interelectrode capacitance. Current flow in this small amount would
not seriously affect circuit performance. On the other hand, at a frequency of 100 megahertz the reactance would
decrease to approximately 1,590 ohms and, with the same voltage applied, current would increase to 315
milliamperes (figure 2-1B). Current in this amount would definitely affect circuit performance.
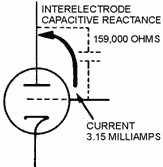
Figure 2-1A. - Interelectrode capacitance in a vacuum tube. 1 MEGAHertz.
2-2
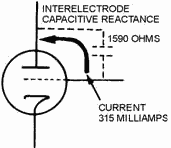
Figure 2-1B. - Interelectrode capacitance in a vacuum tube. 100 MEGAHertz.
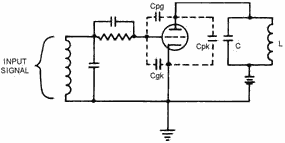
Figure 2-1C. - Interelectrode capacitance in a vacuum tube. Interelectrode Capacitance IN a
Tuned-PLATE Tuned-GRID Oscillator. A good point to remember is that the higher the frequency, or the larger the interelectrode capacitance,
the higher will be the current through this capacitance. The circuit in figure 2-1C, shows the interelectrode
capacitance between the grid and the cathode (Cgk) in parallel with the signal source. As the frequency of the
input signal increases, the effective grid-to-cathode impedance of the tube decreases because of a decrease in the
reactance of the interelectrode capacitance. If the signal frequency is 100 megahertz or greater, the reactance of
the grid-to-cathode capacitance is so small that much of the signal is short-circuited within the tube. Since the
interelectrode capacitances are effectively in parallel with the tuned circuits, as shown in figures 2-1A, B, and
C, they will also affect the frequency at which the tuned circuits resonate. Another frequency-limiting
factor is the LEAD Inductance of the tube elements. Since the lead inductances within a tube are effectively in
parallel with the interelectrode capacitance, the net effect is to raise the frequency limit. However, the
inductance of the cathode lead is common to both the grid and plate circuits. This provides a path for
degenerative feedback which reduces overall circuit efficiency.
2-3
A third limitation caused by tube construction is TRANSIT TIME. Transit time is the time required for
electrons to travel from the cathode to the plate. While some small amount of transit time is required for
electrons to travel from the cathode to the plate, the time is insignificant at low frequencies. In fact, the
transit time is so insignificant at low frequencies that it is generally not considered to be a hindering factor.
However, at high frequencies, transit time becomes an appreciable portion of a signal cycle and begins to hinder
efficiency. For example, a transit time of 1 nanosecond, which is not unusual, is only 0.001 cycle at a frequency
of 1 megahertz. The same transit time becomes equal to the time required for an entire cycle at 1,000 megahertz.
Transit time depends on electrode spacing and existing voltage potentials. Transit times in excess of 0.1 cycle
cause a significant decrease in tube efficiency. This decrease in efficiency is caused, in part, by a phase shift
between plate current and grid voltage. If the tube is to operate efficiently, the plate current must be in phase
with the grid-signal voltage and 180 degrees out of phase with the plate voltage. When transit time approaches 1/4
cycle, this phase relationship between the elements does not hold true. a positive swing of a high-frequency grid
signal causes electrons to leave the cathode and flow to the plate. Initially this current is in phase with the
grid voltage. However, since transit time is an appreciable part of a cycle, the current arriving at the plate now
lags the grid-signal voltage. As a result, the power output of the tube decreases and the plate power dissipation
increases. Another loss of power occurs because of ELECTROSTATIC INDUCTION.
The electrons forming the plate current also electrostatically induce potentials in the grid as they move
past it. This electrostatic induction in the grid causes currents of positive charges to move back and forth in
the grid structure. This back and forth action is similar to the action of hole current in semiconductor devices.
When transit-time effect is not a factor (as in low frequencies), the current induced in one side of the grid by
the approaching electrons is equal to the current induced on the other side by the receding electrons. The net
effect is zero since the currents are in opposite directions and cancel each other. However, when transit time is
an appreciable part of a cycle, the number of electrons approaching the grid is not always equal to the number
going away. As a result, the induced currents do not cancel. This uncancelled current produces a power loss in the
grid that is considered resistive in nature. In other words, the tube acts as if a resistor were connected between
the grid and the cathode. The resistance of this imaginary resistor decreases rapidly as the frequency increases.
The resistance may become so low that the grid is essentially short-circuited to the cathode, preventing proper
operation of the tube. Several methods are available to reduce the limitations of conventional tubes, but
none work well when frequency increases beyond 1,000 megahertz. Interelectrode capacitance can be reduced by
moving the electrodes further apart or by reducing the size of the tube and its electrodes. Moving the electrodes
apart increases the problems associated with transit time, and reducing the size of the tube lowers the
power-handling capability. You can see that efforts to reduce certain limitations in conventional tubes are
compromises that are often in direct opposition to each other. The net effect is an upper limit of approximately
1,000 megahertz, beyond which conventional tubes are not practical.
Q-1. What happens to the impedance of interelectrode capacitance as frequency increases? Q-2. What
undesirable effect is caused by the inductance of the cathode lead? Q-3. How does transit time affect the
relationship of the grid voltage and the plate current at high frequencies? Q-4. Moving tube electrodes
apart to decrease interelectrode capacitance causes an increase in the effect of what property? 2-4
Velocity Modulation The microwave tube was developed when the use of the
frequency spectrum went beyond 1,000 megahertz and into the microwave range. The microwave tube uses transit time
in the conversion of dc power to radio-frequency (RF) power. The interchange of power is accomplished by using the
principle of electron VELOCITY MODULATION and low-loss resonant cavities in the microwave tube. A clear
understanding of microwave tubes must start with an understanding of how electrons and electric fields interact.
An electron has mass and thus exhibits kinetic energy when in motion. The amount of kinetic energy in an electron
is directly proportional to its velocity; that is, the higher the velocity, the higher the energy level. The basic
concept of the electron energy level being directly related to electron velocity is the key principle of energy
transfer and amplification in microwave tubes. An electron can be accelerated or decelerated by an
electrostatic field. Figure 2-2 shows an electron moving in an electrostatic field. The direction of travel (shown
by the heavy arrow) is against the electrostatic lines of force which are from positive to negative. The
negatively charged electron will be attracted to the positively charged body and will increase in velocity. As its
velocity increases, the energy level of the electron will also increase. Where does the electron acquire its
additional energy? The only logical source is from the electrostatic field. Thus, the conclusion is clear. An
electron traveling in a direction opposite to electrostatic lines of force will absorb energy and increase in
velocity (accelerate).
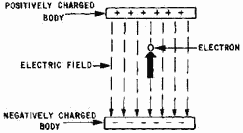
Figure 2-2. - Moving electron gaining velocity and energy. As figure 2-3 illustrates, the opposite condition is also true. An electron traveling in the same
direction as the electrostatic lines of force will decelerate by giving up energy to the field. The negatively
charged body will repel the electron and cause it to decrease in velocity. When the velocity is reduced, the
energy level is also reduced. The energy lost by the electron is gained by the electrostatic field. 2-5
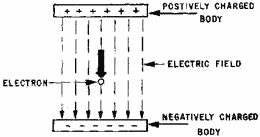
Figure 2-3. - Moving electron losing energy and velocity. The operation of a velocity-modulated tube depends on a change in the velocity of the electrons passing
through its electrostatic field. a change in electron velocity causes the tube to produce BUNCHES of electrons.
These bunches are separated by spaces in which there are relatively few electrons. Velocity modulation is then
defined as that variation in the velocity of a beam of electrons caused by the alternate speeding up and slowing
down of the electrons in the beam. This variation is usually caused by a voltage signal applied between the grids
through which the beam must pass. The first requirement in obtaining velocity modulation is to produce a
stream of electrons which are all traveling at the same speed. The electron stream is produced by an electron gun.
a simplified version of an electron gun is shown in figure 2-4A. Electrons emitted from the cathode are attracted
toward the positive accelerator grid and all but a few of the electrons pass through the grid and form a beam. The
electron beam then passes through a pair of closely spaced grids, called BUNCHER GRIDS. Each grid is connected to
one side of a tuned circuit. The parallel-resonant tuned circuit (figure 2-4A) in the illustration represents the
doughnut-shaped resonant cavity surrounding the electron stream (figure 2-4B). The buncher grids are the dashed
lines at the center of the cavity and are at the same dc potential as the accelerator grid. The alternating
voltage which exists across the resonant circuit causes the velocity of the electrons leaving the buncher grids to
differ from the velocity of the electrons arriving at the buncher grids. The amount of difference depends on the
strength and direction of the electrostatic field within the resonant cavity as the electrons pass through the
grids.
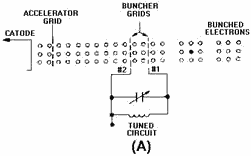
Figure 2-4A. - Electron gun with buncher grids.
2-6
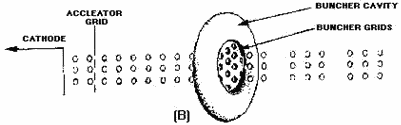
Figure 2-4B. - Electron gun with buncher grids. The manner in which the buncher produces bunches of electrons is better understood by considering the
motions of individual electrons, as illustrated in figure 2-5A. When the voltage across the grids is
negative, as shown in figure 2-5B, electron 1 crossing the gap at that time is slowed. Figure 2-5C shows the
potential across the gap at 0 volts; electron 2 is not affected. Electron 3 enters the gap (figure 2-5D) when the
voltage across the gap is positive and its velocity is increased. The combined effect is shown in figure 2-5E. All
of the electrons in the group have been bunched closer together.
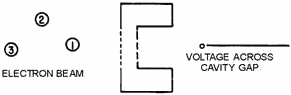
Figure 2-5A. - Buncher cavity action. BUNCHER CAVITY.

Figure 2-5B. - Buncher cavity action. ELECTRON #1 DECELERATED. 2-7

Figure 2-5C. - Buncher cavity action. ELECTRON #2 VELOCITY UNCHANGED.
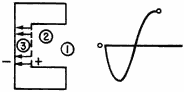
Figure 2-5D. - Buncher cavity action. ELECTRON #3 ACCELERATED.
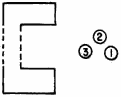
Figure 2-5E. - Buncher cavity action. ELECTRONS BEGINNING to BUNCH, DUE to VELOCITY DifferenceS.
The velocity modulation of the beam is merely a means to an end. No useful power has been produced at
this point. The energy gained by the accelerated electrons is balanced by the energy lost by the decelerated
electrons. However, a new and useful beam distribution will be formed if the velocity- modulated electrons are
allowed to drift into an area that has no electrostatic field. As the electrons drift into the field-free
area beyond the buncher cavity, bunches continue to form because of the new velocity relationships between the
electrons. Unless the beam is acted upon by some other force, these bunches will tend to form and disperse until
the original beam distribution is eventually reformed. The net effect of velocity modulation is to form a
current-density modulated beam that varies at the same rate as the grid-signal frequency. The next step is to take useful power from the beam. The current-modulated (bunched) electron beam in figure 2-6A and B is shown in
various stages of formation and dispersion. a second cavity, called a CATCHER CAVITY, must be placed at a point of
2-8
maximum bunching to take useful energy from the beam (shown in figure 2-6B). The physical position of
the catcher cavity is determined by the frequency of the buncher-grid signal because this signal determines the
transit time of the electron bunches. Note also that both cavities are resonant at the buncher-grid frequency. The
electron bunches will induce an RF voltage in the grid gap of the second cavity causing it to oscillate. Proper
placement of the second cavity will cause the induced grid-gap voltage to decelerate the electron bunches as they
arrive at the gap. Since the largest concentration of electrons is in the bunches, slowing the bunches causes a
transfer of energy to the output cavity. The balance of energy has been disturbed because the placement of the
catcher cavity is such that bunches are slowed down when they arrive at the cavity. The areas between bunches
arrive at the cavity at just the right time. At this time the voltage is of the correct polarity to increase the
velocity of the electrons and the beam absorbs energy. The areas between the bunches have very few electrons, so
the energy removed from the beam is much greater than the energy required to speed up the electrons between the
bunches. Therefore, if the second cavity is properly positioned, useful energy can be removed from a velocity-
modulated electron beam. 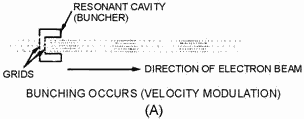
Figure 2-6A. - Removing energy from a velocity-modulated beam.
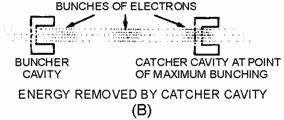
Figure 2-6B. - Removing energy from a velocity-modulated beam. Q-5. The kinetic energy of an electron is directly proportional to what property? Q-6. What
will be the effect upon an electron traveling in the opposite direction to the lines of force in an electrostatic
field? Q-7. How is a beam of electrons velocity-modulated? Q-8. What portion of an electron
gun causes the electrons to accelerate or decelerate?
2-9
Q-9. What is the effect upon an electron that enters the buncher gap when the potential across the
grids is at 0 volts? Q-10. What determines the placement of the catcher cavity?
Microwave TUBES Microwave tubes perform the same functions of generation and amplification in the
microwave portion of the frequency spectrum that vacuum tubes perform at lower frequencies. This section will
explain the basic operation of the most widely used microwave tubes, including klystrons, traveling-wave tubes,
backward-wave oscillators, magnetrons, and crossed-field amplifiers. The variations of these tubes for use in
specific applications are so numerous that all of them cannot be discussed in this module. However, general
principles of operation are similar in all of the variations so the explanations will be restricted to the general
principles of operation. The Basic Two-Cavity Klystron Klystrons are
velocity-modulated tubes that are used in radar and communications equipment as oscillators and amplifiers.
Klystrons make use of the transit-time effect by varying the velocity of an electron beam in much the same manner
as the previously discussed velocity-modulation process. Strong electrostatic fields are necessary in the klystron
for efficient operation. This is necessary because the interaction of the signal and the electron beam takes place
in a very short distance. The construction and essential components of a TWO-CAVITY KLYSTRON are shown in figure
2-7A. Figure 2-7B is a schematic representation of the same tube. When the tube is energized, the cathode emits
electrons which are focused into a beam by a low positive voltage on the control grid. The beam is then
accelerated by a very high positive dc potential that is applied in equal amplitude to both the accelerator grid
and the buncher grids. The buncher grids are connected to a cavity resonator that superimposes an ac potential on
the dc voltage. Ac potentials are produced by oscillations within the cavity that begin spontaneously when the
tube is energized. The initial oscillations are caused by random fields and circuit imbalances that are present
when the circuit is energized. The oscillations within the cavity produce an oscillating electrostatic field
between the buncher grids that is at the same frequency as the natural frequency of the cavity. The direction of
the field changes with the frequency of the cavity. These changes alternately accelerate and decelerate the
electrons of the beam passing through the grids. The area beyond the buncher grids is called the DRIFT SPACE. The
electrons form bunches in this area when the accelerated electrons overtake the decelerated electrons. 2-10
| - |
Matter, Energy,
and Direct Current |
| - |
Alternating Current and Transformers |
| - |
Circuit Protection, Control, and Measurement |
| - |
Electrical Conductors, Wiring Techniques,
and Schematic Reading |
| - |
Generators and Motors |
| - |
Electronic Emission, Tubes, and Power Supplies |
| - |
Solid-State Devices and Power Supplies |
| - |
Amplifiers |
| - |
Wave-Generation and Wave-Shaping Circuits |
| - |
Wave Propagation, Transmission Lines, and
Antennas |
| - |
Microwave Principles |
| - |
Modulation Principles |
| - |
Introduction to Number Systems and Logic Circuits |
| - |
- Introduction to Microelectronics |
| - |
Principles of Synchros, Servos, and Gyros |
| - |
Introduction to Test Equipment |
| - |
Radio-Frequency Communications Principles |
| - |
Radar Principles |
| - |
The Technician's Handbook, Master Glossary |
| - |
Test Methods and Practices |
| - |
Introduction to Digital Computers |
| - |
Magnetic Recording |
| - |
Introduction to Fiber Optics |
| Note: Navy Electricity and Electronics Training
Series (NEETS) content is U.S. Navy property in the public domain. |
|