Module 11 - Microwave Principles: Directional Couplers
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Module 11 − Microwave Principles
Pages i, 1−1, 1−11, 1−21, 1−31, 1−41, 1−51, 1−61, 2−1, 2−11, 2−21, 2−31, 2−41, 2−51, 2−61, 3−1, 3−11, AI−1, Index−1, Assignment 1, Assignment 2
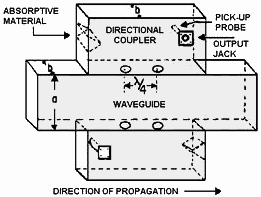
electrolytic corrosion is not taking place. Any waveguide that is exposed to the weather should be painted and all joints sealed. Proper painting prevents natural corrosion, and sealing the joints prevents moisture from entering the waveguide. Moisture can be one of the worst enemies of a waveguide system. As previously discussed, the dielectric in waveguides is air, which is an excellent dielectric as long as it is free of moisture. Wet air, however, is a very poor dielectric and can cause serious internal arcing in a waveguide system. For this reason care is taken to ensure that waveguide systems are pressurized with air that is dry. Checking the pressure and moisture content of the waveguide air may be one of your daily system maintenance duties. Figure 1-53 - Directional coupler - RF Cafe
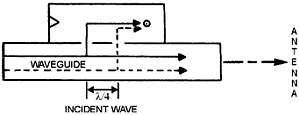
Figure 1-54 - Incident wave in a directional coupler designed to sample incident waves.
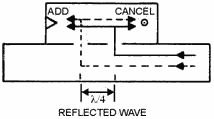
Figure 1-55 - Reflected wave in a directional coupler.
Figure 1-56 - Directional coupler designed to sample reflected energy.
Figure 1-57 - Bidirectional coupler. More detailed waveguide installation and maintenance information can be found in the technical manuals that apply to your particular system. Another good source is the Electronics Installation and Maintenance Handbooks (EIMB) published by Naval Sea Systems Command. Installation Standards Handbook EIMB, NAVSEA 0967-LP-000-0110, is the volume that deals with waveguide installation and maintenance.
Q-41. What is the result of an abrupt change in the size, shape, or dielectric of a waveguide? Q-42. a waveguide bend must have what minimum radius? Q-43. What is the most common type of waveguide joint? Q-44. What is the most likely cause of losses in waveguide systems? Waveguide Devices The discussion of waveguides, up to this point, has been concerned only with the transfer of energy from one point to another. Many waveguide devices have been developed, however, that modify the energy in some fashion during transit. Some devices do nothing more than change the direction of the energy. Others have been designed to change the basic characteristics or power level of the electromagnetic energy. This section will explain the basic operating principles of some of the more common waveguide devices, such as DirectIONAL COUPLERS, CAVITY RESONATORS, and HYBRID JUNCTIONS. Directional Couplers The directional coupler is a device that provides a method of sampling energy from within a waveguide for measurement or use in another circuit. Most couplers sample energy traveling in one direction only. However, directional couplers can be constructed that sample energy in both directions. These are called BIDirectIONAL couplers and are widely used in radar and communications systems. Directional couplers may be constructed in many ways. The coupler illustrated in figure 1-53 is constructed from an enclosed waveguide section of the same dimensions as the waveguide in which the energy is to be sampled. The "b" wall of this enclosed section is mounted to the "b" wall of the waveguide from which the sample will be taken. There are two holes in the "b" wall between the sections of the coupler. These two holes are 1/4λ apart. The upper section of the directional coupler has a wedge of energy-absorbing material at one end and a pickup probe connected to an output jack at the other end. The absorbent material absorbs the energy not directed at the probe and a portion of the overall energy that enters the section. Figure 1-54 illustrates two portions of the incident wavefront in a waveguide. The waves travel down the waveguide in the direction indicated and enter the coupler section through both holes. Since both portions of the wave travel the same distance, they are in phase when they arrive at the pickup probe. Because the waves are in phase, they add together and provide a sample of the energy traveling down the waveguide. The sample taken is only a small portion of the energy that is traveling down the waveguide. The magnitude of the sample, however, is proportional to the magnitude of the energy in the waveguide. The absorbent material is designed to ensure that the ratio between the sample energy and the energy in the waveguide is constant. Otherwise the sample would contain no useful information. The ratio is usually stamped on the coupler in the form of an attenuation factor. The effect of a directional coupler on any reflected energy is illustrated in figure 1-55. Note that these two waves do not travel the same distance to the pickup probe. The wave represented by the dotted line travels 1/2λ further and arrives at the probe 180 degrees out of phase with the wave represented by the solid line. Because the waves are 180 degrees out of phase at the probe, they cancel each other and no energy is induced in the pickup probe. When the reflected energy arrives at the absorbent material, it adds and is absorbed by the material. A directional coupler designed to sample reflected energy is shown in figure 1-56. The absorbent material and the probe are in opposite positions from the directional coupler designed to sample the incident energy. This positioning causes the two portions of the reflected energy to arrive at the probe in phase, providing a sample of the reflected energy. The sampled transmitted energy, however, is absorbed by the absorbent material. A simple bidirectional coupler for sampling both transmitted and reflected energy can be constructed by mounting two directional couplers on opposite sides of a waveguide, as shown in figure 1-57.
Q-45. What is the primary purpose of a directional coupler? Q-46. How far apart are the two holes in a simple directional coupler? Q-47. What is the purpose of the absorbent material in a directional coupler? Q-48. In a directional coupler that is designed to sample the incident energy, what happens to the two portions of the wavefront when they arrive at the pickup probe? Q-49. What happens to reflected energy that enters a directional coupler that is designed to sample incident energy? Cavity Resonators In ordinary electronic equipment a resonant circuit consists of a coil and a capacitor that are connected either in series or in parallel. The resonant frequency of the circuit is increased by reducing the capacitance, the inductance, or both. A point is eventually reached where the inductance and the capacitance can be reduced no further. This is the highest frequency at which a conventional circuit can oscillate. The upper limit for a conventional resonant circuit is between 2000 and 3000 megahertz. At these frequencies, the inductance may consist of a coil of one-half turn, and the capacitance may simply be the stray capacitance of the coil. Tuning a one-half turn coil is very difficult and tuning stray capacitance is even more difficult. In addition, such a circuit will handle only very small amounts of current. NEETS, Module 10, Introduction to Wave Propagation explained that a 1/4λ section of transmission line can act as a resonant circuit. The same is true of a 1/4λ section of waveguide. Since a waveguide is hollow, it can also be considered as a RESONANT CAVITY. By definition, a resonant cavity is any space completely enclosed by conducting walls that can contain oscillating electromagnetic fields and possess resonant properties. The cavity has many advantages and uses at microwave frequencies. Resonant cavities have a very high Q and can be built to handle relatively large amounts of power. Cavities with a Q value in excess of 30,000 are not uncommon. The high Q gives these devices a narrow bandpass and allows very accurate tuning. Simple, rugged construction is an additional advantage. Although cavity resonators, built for different frequency ranges and applications, have a variety of shapes, the basic principles of operation are the same for all.
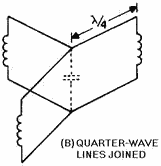
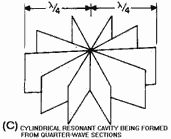
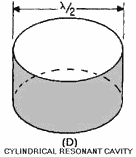
Figure 1-58A - Rectangular waveguide cavity resonator.
Figure 1-58B - Rectangular waveguide cavity resonator.
Figure 1-60 - Several types of cavities. One example of a cavity resonator is the rectangular box shown in figure 1-58A. It may be thought of as a section of rectangular waveguide closed at both ends by conducting plates. The frequency at which the resonant mode occurs is 1/2λ of the distance between the end plates. The magnetic and electric field patterns in the rectangular cavity are shown in figure 1-58B. Field Patterns of a Simple Mode The rectangular cavity is only one of many cavity devices that are useful as high-frequency resonators. Figures 1-59A, 1-59B, 1-59C, and 1-59D show the development of a cylindrical resonant cavity from an infinite number of quarter-wave sections of transmission line. In figure 1-59A the 1/4λ section is shown to be equivalent to a resonant circuit with a very small amount of inductance and capacitance. Three 1/4λ sections are joined in parallel in figure 1-59B. Note that although the current-carrying ability of several 1/4λ sections is greater than that of any one section, the resonant frequency is unchanged.
Figure 1-59A. - Development of a cylindrical resonant cavity.
Figure 1-59B - Development of a cylindrical resonant cavity.
Figure 1-59C - Development of a cylindrical resonant cavity.
Figure 1-59D - Development of a cylindrical resonant cavity. This occurs because the addition of inductance in parallel lowers the total inductance, but the addition of capacitance in parallel increases the total capacitance by the same proportion. Thus, the resonant frequency remains the same as it was for one section. The increase in the number of current paths also decreases the total resistance and increases the Q of the resonant circuit. Figure 1-59C shows an intermediate step in the development of the cavity. Figure 1-59D shows a completed cylindrical resonant cavity with a diameter of 1/2λ at the resonant frequency. Quarter-Wave Section Equivalent to LC Circuit Refer to Figure 1-59B. Quarter-Wave Lines Joined Refer to Figure 1-59C. Cylindrical Resonant Cavity Being Formed from Quarter-Wave Sections Refer to Figure 1-59D. Cylindrical Resonant Cavity There are two variables that determine the primary frequency of any resonant cavity. The first variable is PHYSICAL SIZE. In general, the smaller the cavity, the higher its resonant frequency. The second controlling factor is the SHAPE of the cavity. Figure 1-60 illustrates several cavity shapes that are commonly used. Remember from the previously stated definition of a resonant cavity that any completely enclosed conductive surface, regardless of its shape, can act as a cavity resonator.
Figure 1-61 - Rectangular cavity resonator.
Figure 1-62. - Cavity tuning by volume.
Figure 1-63A - Methods of changing the resonant frequency of a cavity.
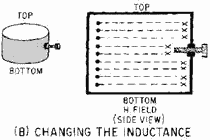
Figure 1-63B - Methods of changing the resonant frequency of a cavity. Cavity resonators are energized in basically the same manner as waveguides and have a similar field distribution. If the cavity shown in figure 1-61 were energized in the TE mode, the electromagnetic wave would reflect back and forth along the Z axis and form standing waves. These standing waves would form a field configuration within the cavity that would have to satisfy the same boundary conditions as those in a waveguide. Modes of operation in the cavity are described in terms of the fields that exist in the X, Y, and Z dimensions. Three subscripts are used; the first subscript indicates the number of 1/2λ along the X axis; the second subscript indicates the number of 1/2λ along the Y axis; and the third subscript indicates the number of 1/2λ along the Z axis. Energy can be inserted or removed from a cavity by the same methods that are used to couple energy into and out of waveguides. The operating principles of probes, loops, and slots are the same whether used in a cavity or a waveguide. Therefore, any of the three methods can be used with cavities to inject or remove energy. The resonant frequency of a cavity can be varied by changing any of three parameters: cavity volume, cavity capacitance, or cavity inductance. Changing the frequencies of a cavity is known as TUNING. The mechanical methods of tuning a cavity may vary with the application, but all methods use the same electrical principles. A mechanical method of tuning a cavity by changing the volume (VOLUME TUNING) is illustrated in figure 1-62. Varying the distance d will result in a new resonant frequency because the inductance and the capacitance of the cavity are changed by different amounts. If the volume is decreased, the resonant frequency will be higher. The resonant frequency will be lower if the volume of the cavity is made larger. Capacitive Tuning of a cavity is shown in figure 1-63A. An adjustable slug or screw is placed in the area of maximum E lines. The distance d represents the distance between two capacitor plates. As the slug is moved in, the distance between the two plates becomes smaller and the capacitance increases. The increase in capacitance causes a decrease in the resonant frequency. As the slug is moved out, the resonant frequency of the cavity increases. Changing the Capacitance Refer to Figure 1-63A Changing the Inductance INDUCTIVE TUNING is accomplished by placing a nonmagnetic slug in the area of maximum H lines, as shown in figure 1-63B. The changing H lines induce a current in the slug that sets up an opposing H field. The opposing field reduces the total H field in the cavity, and therefore reduces the total inductance. Reducing the inductance, by moving the slug in, raises the resonant frequency. Increasing the inductance, by moving the slug out, lowers the resonant frequency. Resonant cavities are widely used in the microwave range, and many of the applications will be studied in chapter 2. For example, most microwave tubes and transmitting devices use cavities in some form to generate microwave energy. Cavities are also used to determine the frequency of the energy traveling in a waveguide, since conventional measurement devices do not work well at microwave frequencies.
Q-50. What two variables determine the primary frequency of a resonant cavity? Q-51. Energy can be inserted or removed from a cavity by what three methods? Q-52. Inductive tuning of a resonant cavity is accomplished by placing a nonmagnetic slug in what area? Waveguide Junctions You may have assumed that when energy traveling down a waveguide reaches a junction, it simply divides and follows the junction. This is not strictly true. Different types of junctions affect the energy in different ways. Since waveguide junctions are used extensively in most systems, you need to understand the basic operating principles of those most commonly used. The T JUNCTION is the most simple of the commonly used waveguide junctions. T junctions are divided into two basic types, the E-TYPE and the H-TYPE. HYBRID JUNCTIONS are more complicated developments of the basic T junctions. The MAGIC-T and the HYBRID RING are the two most commonly used hybrid junctions. E-TYPE T JUNCTION. - An E-type T junction is illustrated in figure 1-64, view (A). It is called an E-type T junction because the junction arm extends from the main waveguide in the same direction as the E field in the waveguide.
Related Pages on RF Cafe
Posted July 28, 2021 |
||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||
  |
 |
|
Please Support RF Cafe by purchasing my ridiculously low−priced products, all of which I created.
These Are Available for Free |
|
|
About RF Cafe
Copyright: 1996 - 2024 Web BSEE - KB3UON RF Cafe began life in 1996 as "RF Tools" in an AOL screen name web space totaling 2 MB. Its primary purpose was to provide me with ready access to commonly needed formulas and reference material while performing my work as an RF system and circuit design engineer. The World Wide Web (Internet) was largely an unknown entity at the time and bandwidth was a scarce commodity. Dial-up modems blazed along at 14.4 kbps while tying up your telephone line, and a nice lady's voice announced "You've Got Mail" when a new message arrived... All trademarks, copyrights, patents, and other rights of ownership to images
and text used on the RF Cafe website are hereby acknowl My Hobby Website: |
|
