|
The thyratron is not necessarily
a familiar type of vacuum tube to most RF and microwave electronics practitioners
unless they happen to be involved in radar, imaging (x-ray), particle accelerators,
etc.† It is basically a high speed, high current switch used in
pulse forming networks for firing magnetrons (via a high-voltage transformer). Both
the S-band airport surveillance radar and the X-band precision approach radar I
worked on in the USAF employed thyratrons. The X-band radar had been modified by
the time I came on the scene to use a solid state thyratron (one of the earliest
adaptations), but the S-band radar still used its original vacuum tube thyratron.
While I don't recall for certain, I
 believe the thyratron in the thumbnail image
is the one it used. The accompanying ruler is 12" long to give you an idea of the
size. They used to burn out and have to be replaced fairly regularly on our mobile
radar units probably from being powered up and down so often, and from the occasional
over-the-road trip en route to a temporary runway believe the thyratron in the thumbnail image
is the one it used. The accompanying ruler is 12" long to give you an idea of the
size. They used to burn out and have to be replaced fairly regularly on our mobile
radar units probably from being powered up and down so often, and from the occasional
over-the-road trip en route to a temporary runway
 location. location.
Being a lifelong electronics nerd and woodworker, I actually made a lamp out
of a spent S-band thyratron tube (no photo, unfortunately). I turned an oak base
on a lathe and then mounted the tube in the middle. Three 3/8" diameter brass tubes
were bent to conform to the side of the vacuum tube and were joined with a brass
strip at the top. A threaded lamp socket nipple went in the middle of the junction
and the entire assembly was soldered. The bottoms of the tubes were epoxied into
holes in the wood base spaced 120° apart around the tube's perimeter. The lamp
cord was threaded through one of the brass tubes and routed out the side of the
base to a plug. The bulb socket and harp for holding the shade topped off the lamp.
My parents were the lucky recipients. While I regarded it as a fine example of artistic
juxtaposing of classic wood and modern microwave electronics, they likely considered
it as fitting for public display as Ralphie's mother did the "major award" his father
won from an entry in a crossword puzzle contest which was the lady's fishnet-stockinged
leg lamp (A Christmas Story). My lamp's current status is MIA - probably
buried in the back yard like Mr. Paker's lamp.
† RF Cafe visitor Jimmy C. pointed out another common use of
the thyratron, "I would like to add Television Broadcast Transmitters using
IOTs.
The purpose of the thyratron is to remove the DC High Voltage from the IOT when
there is an arc. The Thyratron actually shorts the high voltage to ground. Not sure
how it handles 32,000 volts to ground but it does. It operates very fast. That is
how it protects the IOT from damage."
A Portable Thyratron Tester
By W. Philbrook

Figure 1 - The Alectric thyratron tester.
A commercially available instrument uses several unique circuits to test specialized
tube types.
There are receiving tube checkers of almost every conceivable variety on the
market but there has been no portable, easily usable tester for thyratron tubes.
Why this condition has existed is difficult to say because, with the volume of industrial
electronic equipment in current use, there should be an excellent sales potential
for such a device. Now a tester has been developed which not only permits the rapid
and accurate checking of a thyratron tube's characteristics, but does so with a
number of unique circuits. Before we examine these circuits, it may be desirable
to review the basic operation of a thyratron tube.
Thyratrons are gas-filled tubes in which the flow of current is either at zero
or at the saturation value. The grid voltage, usually negative, keeps them cut off
until such time as it is desired to trigger them. At that time, the grid voltage
is made relatively positive and electrons are thus permitted to flow from the cathode
to the plate.
Once this movement starts, even in a minute degree, the molecules of gas enclosed
in the tube tend to become positively ionized. This condition of positive ionization
neutralizes the holding or controlling voltage on the grid. This action completely
opens the dam, so to speak, to the electrons being emitted by the cathode and permits
current to surge freely through the tube to the plate. Once this flow has started,
the grid loses all control over the rate of flow and - as long as the plate voltage
is kept above a certain critical minimum - all electrons leaving the cathode travel
to the plate.
This, roughly, is how a thyratron tube operates. And to determine the operating
condition of such a tube obviously requires a special type of tester. Let us therefore
note the various thyratron features which are important and see how the tester shown
in Fig. 1, made by the Alectric Mfg. Co. of Kenosha, Wis., accomplishes its
testing function.
One of the first things to observe is that most thyratrons operate with alternating
voltage on the plate (or anode). This is done so that the grid may resume control
of the tube after it has been fired or triggered. There is no point in having a
tube in the circuit over which no control at all is possible, and the simplest way
to achieve this control is to apply a.c. to the plate. When the plate voltage goes
negative, conduction ceases, the ionized gas de-ionizes, and the control grid is
able to prevent the flow of electrons from cathode to plate. The tube is now ready
for the next triggering pulse.

Figure 2 - Complete schematic for the Alectric specialized thyratron
tester.
Hence, if you examine the schematic diagram of this tester, Fig. 2, you
will see that a.c. voltage is brought to the plate from one of two points: either
the variable-voltage transformer, T1
or the step-up transformer, T3. Voltages
from 0 to 200 volts are obtainable from T1
while 0 to 3000 volts (peak) can be obtained from the secondary of T3. The purpose of the low a.c. voltage is to check
thyratrons at their rated currents - in this case, either 1, 2.5, or 6 amperes.
By using a low voltage and proportionately low-valued resistors in the plate circuit,
the wattage requirement and, with it, the heat dissipation can be kept within reasonable
bounds. When checking 2.5 and 6 ampere tubes, even under these conditions, it is
still necessary to place the plate load resistors in a separate box. If a higher
plate voltage were used, the load resistances would be correspondingly higher and
the wattage requirements would raise the cost of these units excessively. Hence,
low plate voltages are used for certain tests where maximum rated anode currents
are desired.
On the other hand, when a thyratron tube is being checked for its grid-plate
characteristics, we can use a high plate voltage and employ high-valued load resistances
in the plate circuit to keep the current down. In this test, it is simply a question
of establishing "trigger points" or critical grid voltages, not to determine what
the peak plate current is. More on this test presently.
The path of the a.c. voltage from T1
to the plate of the thyratron tube to be checked can be readily followed from Fig. 2.
The start can be made at T1. From the
center tap, point B, the line leads to switch S2,
which for the purpose of this test is turned to the a.c. position. From S2, the path goes to point C, then through S2-4, which is now closed, to point D, then E, and
finally through R7 to the plate of the
thyratron. The other side of the circuit is completed from point A through S1-2, which is now closed, to F and from here to
the center tap of the filament transformer, T5.
Arc-Drop Test
Now, as a measure of tube reliability, a direct measurement is not made of the
tube's peak plate current. Rather we measure the voltage drop across the tube when
the latter is conducting at full current. This voltage is known as the arc drop
and its value is sought because an increase in the arc-drop voltage is the most
outstanding indication of the end of life of a thyratron tube. However, a single
arc-drop reading in itself will not indicate the life factor; rather what is needed
is a series of readings over a period of time to anticipate the end. See Fig. 3.
The technique could, in a way, be compared to the predicting of weather conditions
by taking comparative readings on a barometer.
It is suggested that a reading be taken after about every 400 hours of operation.
As the arc-drop value begins to rise, a shorter interval should be observed - say
every 200 hours as the tube approaches the end of its useful life.

Figure 3 - The arc-drop voltage of a thyratron increases generally
with the age of the tube, but may vary during life. It is an indication of tube
condition.
To be most effective, the arc-drop reading permits the end of life to be predicted
so that the tube can be removed from operation before costly work stoppage occurs.
A reasonable amount of arc-drop may well establish the limits at which such tubes
should be removed to prevent emergency shut-downs.
Once a tube is placed in operation, its arc-drop voltage will vary throughout
its life. Typical variations are shown in Fig. 3. With tube "C" the rate of
increase of the arc drop accelerates, but the curve is easily recognized. As a result,
the tube can be replaced before this reading reaches its published limit. The steady
linear rise with tube "B" is also easily recognized. As happens with some tubes,
the limit is reached early with tube "A" but this condition is only temporary. The
arc-drop voltage reduces below the limit again. However, the upward rise is soon
resumed, so the tube should be changed the first time the limit is reached.
When measuring the arc-drop voltage, simply placing an a.c. voltmeter across
the tube would produce an erroneous indication. This is because on one half-cycle,
when the tube is conducting, we would be measuring the true arc-drop value; however,
on the other half-cycle, when the tube is non-conducting, the meter would be subject
to the full applied a.c. voltage. The average of these two readings would be much
higher than the true arc-drop value.
In the Alectric tester, this difficulty is overcome by inserting the current
coil of a wattmeter in series with the plate of the tube to be checked, while the
voltage coil of the meter is placed across the tube, from plate to cathode. Since
tube current flows only during one half-cycle, the wattmeter will be affected only
during this period. During the subsequent negative half-cycle, no plate current
flows, the current coil is inactive, and the meter is not actuated. Furthermore,
the plate circuit resistance is so chosen that only 1 ampere flows through the current
coil. This permits the meter scale to be calibrated directly in volts representing
the arc-drop voltage. Additional switches (S3
and S4) and load resistors (R17 and R18)
permit tubes with plate currents up to 6 amperes to be checked. (Although 6 amperes
is the maximum current available, tubes through the 16-ampere rating are tested
at the 6-ampere level.)
Critical Anode Voltage
Another characteristic of a thyratron is its critical anode starting voltage.
This test is made at a specified control-grid voltage, usually on the order of 4
volts positive on the grid. The anode voltage, which is d.c. now, is slowly increased
from zero until the firing point of the tube is reached. This value can be compared
to that given by the manufacturer. Most of the time, the tube-data sheet will list
the anode starting voltage for an average tube of a given type and also for the
tube within the type with the highest starting voltage.
The d.c. voltage required for this test is obtained from selenium rectifier SR1, resistor R4
and filter capacitor C1. For the test,
S2 is placed in the d.c. position and
the d.c. voltage developed across C1
is fed, via S1-4 to the anode of the
thyratron tube to be tested. (S1-4 is
closed for this test.) The voltmeter is placed in the position indicated by the
dotted lines from the anode of the tube, through R37 and R16.
Readings are taken on the low 100-volt scale, since the anode starting voltage seldom
exceeds 50 or 60 volts when the control grid is 4 volts positive.
The necessary positive grid voltage for the thyratron is obtained from the network
consisting of T4 the two selenium rectifiers
connected across T4 R26, C6
R25 and R24. The control grid is directly connected to the
center tap of R24. The center arm of
R-g; goes to the filament of the thyratron via a center tap on filament transformer
T •. When the movable arm of R25, is
exactly at its center position, there will be no difference of potential between
the grid and filament. Turning the arm of R25
in one direction produces a nega\tive grid potential; rotating the arm in the opposite
direction produces a positive grid voltage. This arrangement is simple and quite
effective.
Critical Grid Voltage
To understand the purpose of the next test, that of determining the critical
grid voltage, let us refer to a tube characteristic chart. This is shown in Fig.
4 for a C3J tube, but it is typical in form for a wide variety of thyratrons. In
the section of the graph labeled "No Breakdown In This Area," no combination of
certain a.c. anode voltages on the left-hand side with certain negative grid voltages
shown at the bottom will cause the tube to fire. To reach the firing point of a
tube, we must move into the shaded area. Some tubes may have to be driven deeper
into this area (meaning either higher plate voltages or less negative grid voltages)
before they are triggered, but they should fire before they reach the extreme right-hand
edge of the shaded section. If this does not occur, some defect or variation from
normal is indicated and the tube should be replaced.
Beyond the shaded area and to the right of it, the control grid is generally
so positive that almost any positive anode voltage will trigger the tube. Operation
in this area is not sought because control of the tube is either difficult, variable,
or impossible.
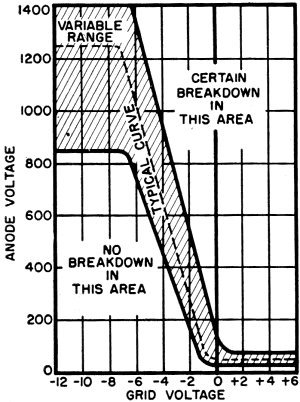
Figure 4 - Tube characteristic chart for the C3J, a typical thyratron,
shows the range of combinations of grid and anode voltages that will cause firing,
also the combinations of these voltages that will cause breakdown of the tube.
To test a thyratron tube for its critical grid voltage, high-valued a.c. anode
voltages are required. These are obtained from the secondary of transformer T3, where voltages having r.m.s. values to 1500
volts are available. In carrying out this test, S1-1
and S1-3 are closed, while S1-2 and S1-4
are open. Switch S2 is in the a.c. position.
The voltage developed across the secondary winding of T3 reaches the plate of the test thyratron via R5 and R7.
R5 is purposely made high in value so
that the anode current will be kept below 40 ma. This is done because there is no
desire to check the ability of the tube to produce its peak current; rather, all
we wish to do is determine its critical grid voltage at a certain anode voltage.
By keeping the current low, it is possible to use a low-wattage, inexpensive resistor
for R5. We obtain the same value for
the critical grid voltage whether a large or a small current flows after the tube
has been triggered.
Now to the test itself. It could be carried out by fixing the anode voltage at
some value and then slowly reducing the negative grid voltage-making it more positive
- until the tube fires. This would be done by slowly rotating R25 until the neon light in the plate circuit flickered
on.
However, the same characteristic can be determined automatically because of the
presence of C3 and R38. Initially, R25
is set until it is 4 volts positive with respect to the filament. The a.c. anode
voltage is then slowly increased until the tube fires. When this happens, the surge
of current through the circuit charges C3,
counteracting the initial +4 volts on the grid. During the next positive half-cycle
of a.c. anode voltage, the tube firing point is governed by the combined voltage
from R25 and C3. This combination, after a few cycles, attains
an equilibrium level which is the critical grid voltage for that value of applied
anode voltage.
If we now change the anode voltage, by adjusting T1, then the total grid-to-filament voltage will
reestablish itself at another equilibrium value which will represent the critical
grid voltage for that anode voltage. For example, if the anode voltage is raised,
the voltage across C3 will increase,
effectively making the grid-to-filament potential more negative than it was before.
Conversely, if the anode voltage is lowered, the average voltage developed across
C3 will decrease.
In essence, the network formed by C3,
R38 , and R25 swings the tube's operating point a minute distance
above and below the firing point. The range is governed by the values of these components
(i.e., the overall time constant). Here it is chosen so that the meter needle recording
the critical grid voltage remains quite steady as the anode voltage passes through
its positive and negative half-cycles.
Critical Grid Current
The final characteristic of the tube to be checked is the critical grid current.
This is the infinitesimal grid current that flows as the critical grid voltage is
approached. It starts at the grid and flows down through R22 when push-button PB7 is opened. The voltage developed across R22 is negative on the grid side of the resistor
and positive on the other side. Furthermore, this voltage adds to that provided
by R25 and C3.
To see how this critical current itself is measured, note first that R22 is a 1-megohm resistor. Since the critical grid
current is in microamperes, the value of voltage developed across R22 is equal to the grid current in microamperes.
When PB7 is closed, and the system is
set up so that the critical grid voltage is indicated automatically, then the value
of the total grid voltage is revealed by the grid voltmeter. This meter is connected
between the bottom of R22 (and hence
is not affected by any voltage that may develop across R22) and the center tap of the filament transformer.
If, now, PB7 is opened, the critical
grid current will flow through R22 and
develop several volts here. This will alter the total grid-to-filament potential
and drive the grid more negative. To bring the overall voltage back to the critical
grid value point, the voltage across C3
will decrease by an amount equal to that brought into the circuit by R22.
This change in C3 voltage will be
reflected in the grid voltmeter reading since the latter, remember, measures both
C3 voltage and that developed by R25. Thus, the change in reading on the grid voltmeter
when PB7 is depressed represents the
critical grid current in microamperes.
This covers the operation of the tester in general and the tests it performs.
Some odds and ends still remain, such as the VR-150 which is placed in parallel
with C3. This tube serves to protect
C3 when switch S8 is first opened and C3 is being charged initially. Voltage surges of
a thousand volts or more frequently occur at this time. These would destroy C3 unless the latter had a sufficiently high breakdown
voltage value. Since C3 possesses a
high capacitance, using a unit with a high surge rating would be extremely costly.
The difficulty is solved much more economically by having the VR-150 tube as protection.
In the anode voltmeter circuit at the left, four ranges are obtained using only
three push-buttons. With all buttons open, the voltmeter is on its 2000-volt range.
For the 1000-volt range, the button so marked is depressed. The same is true for
the 100- and 200-volt ranges; that is, the desired range is brought in by depressing
the associated button. The circuit is so set up that, when either the 1000- or 2000-volt
ranges are in use, depressing the 100- or 200-volt buttons accidentally will have
no effect on the meter.
This tester will also check phanotron tubes. These are tubes which are essentially
thyratrons without a control grid. Hence, the tests are considerably simplified
for them. Tests usually include arc-drop voltage, anode starting voltage, and an
interelement short-circuit check.
The prime purpose of any tube tester or analyzer is to permit a decision to be
made on the condition of the tube. It is not a practical matter to construct a tester
like the conventional radio-tube tester where a meter reads "good" or bad." In a
thyratron, there are many factors other than the tube's ability to conduct a given
quantity of current that determine its acceptance. That is why all of the foregoing
tests are provided for and all should be performed if a true picture of condition
is to be achieved.
Posted February 13, 2020
(updated from original post on 9/30/2013)
|














