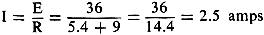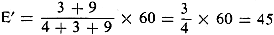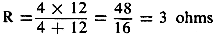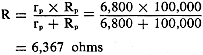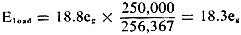|
October 1962 Radio-Electronics
 [Table of Contents] [Table of Contents]
Wax nostalgic about and learn from the history of early electronics.
See articles from Radio-Electronics,
published 1930-1988. All copyrights hereby acknowledged.
|
Thévénin's Theorem is a
fundamental concept in electrical engineering that simplifies complex linear electrical
networks into simpler, equivalent circuits. It's named after the French engineer
Léon Charles Thévénin, who formulated the theorem. Thévénin's Theorem is particularly
useful for analyzing and solving circuits with multiple components and sources.
The theorem states that any linear electrical network with multiple sources and
resistive elements can be replaced by a single voltage source (Thévénin voltage)
in series with a single resistor (Thévénin resistance). This simplified equivalent
circuit is called the Thévénin equivalent circuit. This article from a 1962 issue
of Radio-Electronics magazine presents a great introduction to the basics
of Thévénin's Theorem.
Make Complex Problems Simple
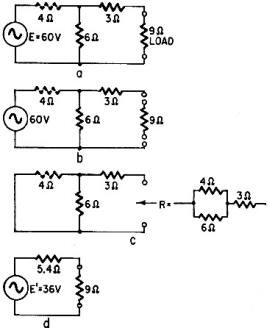
Fig. 1 - Series-parallel circuit. b - To calculate E' we open-circuit
the load. c - To calculate R, look at the circuit from load end with generator shorted.
d - Simplified equivalent circuit.
Thevenin's theorem simplifies circuit analysis for matching impedance and calculating
distribution systems.
By John R. Collins
While no single method of analysis is ideal for all purposes, Thevenin's theorem
provides solutions for many types of problems. Telephone engineers use it to match
impedances in communication networks, and power engineers to simplify complex distribution
systems. It has many applications to electronic circuits, too, and electronics technicians
will find it offers a new tool for solving radio problems.
Basically, Thevenin's theorem is a method of reducing a complicated network to
a simple circuit consisting of a voltage source and series impedance. It is applicable
to both ac and dc circuits in steady-state operation and, although only resistors
are used in the examples which follow, the system works equally well with circuits
containing capacitors, transformers and coils. The method is clear and direct-you
never have to wonder how to begin. A complicated circuit is converted to a simple
circuit in two steps:
First: To find the voltage of the new circuit, disconnect the
load and calculate the voltage appearing across the load terminals of the original
circuit.
Second: To find the series impedance of the new circuit,
remove the voltage source (or sources, if there are more than one) from the original
circuit, replace it with an impedance equal to the internal impedance of the voltage
source, and calculate the impedance that the load "sees." (If internal impedance
is negligible, the voltage source can be replaced with a short circuit.)
Application to Circuits
The method is illustrated with the network in Fig. l-a, a series-parallel resistive
circuit. The source is a 60-volt generator that has an internal resistance of 4
ohms, shown here as a series resistor. The load is a 9-ohm resistor.
As a first step, we disconnect the load (Fig. 1-b) and calculate the voltage
across the load terminals. With the load open-circuited, no current flows through
the 3-ohm resistor. The voltage at the load terminals, therefore, is equal to the
voltage drop across the 6-ohm resistor. Since the entire 60-volt source is dropped
across 10 ohms (that is, 6 ohms + 4 ohms), the voltage drop across each ohm is 60
divided by 10, or 6 volts. Across the 6-ohm resistor, then, the voltage drop is
36 volts, and this becomes the voltage of the new circuit, which we designate E'.
Stated another way, since 6 ohms represents 6/10 of the total series resistance,
6/10 of the source voltage will be dropped across it. This calculation can be simply
expressed as follows:

As a second step, the voltage source is removed, replaced by a connecting wire
(Fig. 1-c), and the impedance is calculated looking from the load terminals. This
operation places the 4- and 6-ohm resistors in parallel, and their equivalent resistance
is found by dividing their product by their sum. Thus,

When this equivalent resistance is added to the 3-ohm series resistance, we obtain
a total resistance (looking from the load terminals) of 5.4 ohms.
The new circuit resulting from the above calculations appears in Fig. 1-d. It
is a simple circuit made up of a 36-volt source and a 5.4-ohm resistor in series
with the 9-ohm load resistor. The current through the load is readily calculated
by Ohm's law:
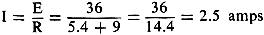
If you analyze the original circuit, you will find that the current through the
9-ohm resistor is also 2.5 amperes, so the two circuits are equivalent as far as
the load is concerned. Although we are usually interested primarily in the effect
on the load, it is sometimes objected that Thevenin's theorem gives a limited picture
of circuit performance, since it presents the circuit only from the standpoint of
the load.
This objection is at least partly overcome by the fact that any circuit element
can be selected to be the load.
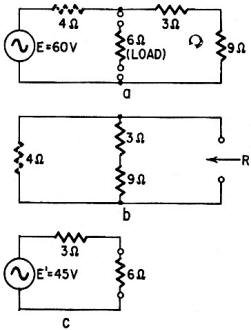
Fig. 2 - Here we use the same circuit arrangement as in Fig.
1, but assume the 6-ohm resistor as the load.
Fig. 2 shows how the same circuit would be handled if we consider the 6-ohm resistor
as the load. With the load open-circuited (Fig. 2-a), the voltage appearing at its
terminals is equal to the voltage drop across the 3- and 9-ohm resistor combination.
Since the combination represents 12/16, or 3/4, of the total series resistance,
we multiply this fraction by the circuit voltage, as in the previous example:
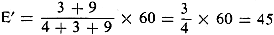
The next step is to remove the voltage source, replace it with a connecting wire,
and calculate the impedance looking from the load. The circuit is redrawn in Fig.
2-b to show how this is done. Replacing the voltage source by a connecting wire
brings the 4-ohm resistor in parallel with 12 ohms, made up of the 3- and 9-ohm
resistor combination. The equivalent resistance is calculated as the product divided
by the sum:
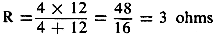
The equivalent circuit (from the standpoint of the 6-ohm resistor) is shown in
Fig. 2-c - a 45-volt source connected to the load through a 3-ohm resistor. The
load current, computed by Ohm's law, is 5 amperes.
Impedance Matching
We mentioned earlier that Thevenin's theorem is often used for impedance matching.
It can be proved (though we won't do it again here) that maximum power is transferred
to the load when the load resistance equals the internal circuit resistance. In
the first example, therefore, maximum power would be transferred if a 5 A-ohm load
were used instead of the 9-ohm load, and in the second example if a 3-ohm load were
used. This kind of analysis is of great importance in designing telephone and other
networks where small signals must be handled economically.
If the internal impedance of the circuit is made up of both resistance and reactance,
maximum power is transferred when the load resistance is equal to the circuit resistance,
and the load reactance is equal but opposite to the circuit reactance. This means
that if the circuit reactance is inductive, the load reactance should be capacitive
for maximum power transfer. This principle is illustrated in Fig. 3.
Electron-Tube Circuits
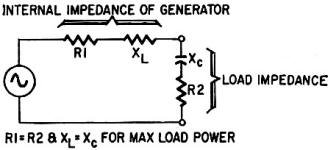
Fig. 3 - Impedance matching for maximum power transfer.
Thevenin's theorem is applied to electron-tube circuits by replacing the tube
with a generator having a voltage equal to μeg, where μ is the
amplification factor of the tube, and eg is the signal voltage applied
to the grid. The dynamic plate resistance rp of the tube constitutes
the internal resistance of the generator.
To illustrate this method, let's consider the amplifier stage shown in Fig. 4-a.
consisting of a triode tube (half a 6SN7) connected in the conventional way. If
the tube is replaced by an equivalent generator, the circuit can be redrawn as in
Fig. 4-b. The values of μ (20) and of rp (6,800) we obtain from a
tube manual. For simplicity, we assume that the amplifier operates in the mid-frequency
range where the reactance of capacitor C is negligible.
***
This Is Thevenin's Theorem
The current in a terminating impedance connected to any network is the same as
if the network were replaced by a generator with a voltage equal to the open-circuit
voltage of the network, and whose internal impedance is the impedance seen by the
termination looking back into the network. All generators in the network are replaced
with impedances equal to the internal impedance of these generators.
***
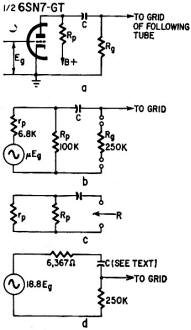
Fig. 4a - Resistance-coupled amplifier stage. b-Modified circuit.
c - Calculation of the series resistance. d - Equivalent circuit.
Following the procedure outlined above, we first disconnect the load (in this
case, the grid-leak resistor Rg) and calculate the voltage across its
terminals, which will be equal to the drop across Rp. The source voltage
is 20eg (that is, 20 times whatever signal voltage is applied to the
grid), and it is in series with rp and Rp. The drop across
Rp, then, is in proportion to the fraction.
Rp/(rp + Rp)
The voltage of the new circuit is calculated as in previous examples:

This means that the voltage of the new circuit will be 18.8 times whatever voltage
is applied to the grid.
Next we remove the generator from the circuit, replace it with a connecting wire,
then calculate the circuit resistance as it appears to the load (Fig. 4-c). This
computation is made as in previous examples:
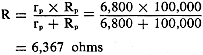
Slide-rule accuracy is enough for this purpose, and the calculation can be made
rapidly. The final circuit is shown in Fig. 4-d.
In previous examples, we calculated the current through the load. In an amplifier,
however, we are more concerned about the voltage drop across the load. This is found
by determining the fraction of total resistance represented by the load resistance,
and multiplying that fraction by the source voltage. Since in this instance the
fraction 250,000/256,367, it is obvious that practically all the voltage will be
dropped across the load - which is as it should be. The actual amount can be computed
with the slide rule:
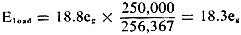
This means that if, say, a signal of 0.5 volt is applied to the grid, the voltage
across the load resistor will be 18.3 x 0.5, or 9.15 volts.
If the reactance of the capacitor is not negligible at the operating frequency,
it must be calculated from the formula, Xe = 1/(2πfC) and considered
in series with the load resistor. If this reactance is large, a large part of the
voltage will be dropped across it instead of the load resistor. This will curtail
the amplification seriously. The remedy, of course, is to use a larger coupling
capacitor.
You will notice that no attempt was made to match the load resistor to the circuit
resistance to obtain maximum power transfer. To do so would greatly reduce the voltage
amplification, even though the power transfer would be increased, and in this instance
we are primarily concerned with obtaining a high output voltage.
Posted September 13, 2024
|