|
February 1952 Radio-Electronics
 [Table of Contents] [Table of Contents]
Wax nostalgic about and learn from the history of early electronics.
See articles from Radio-Electronics,
published 1930-1988. All copyrights hereby acknowledged.
|
 Although this "Algebra in Electronic Design"
article in the February 1952 issue of Radio-Electronics magazine does not
claim to be the second part of author Edmund Berkeley's "Light Sensitive Electronic
Beast" article from the previous December's issue, it does help to know that the
"Squee" mentioned here came from there. Squee is a Robot Squirrel which has four
sensing organs, three acting organs, and a small electronic and relay brain. "Although
Squee is not a very clever robot, he does have a small amount of memory and of reasoning
ability." Boolean logic (aka Boolean algrbra), a common part of modern electronic
circuits and systems, was a relatively new concept only recently adopted from the
field of theoretical mathematics for use in digital computers. Applications were
basic AND, OR, and NOT "gates" comprised of discrete diodes (and vacuum tubes at
that) since transistors and solid state diodes had only been commercially available
for a couple years. In fact, solid state diode schematic symbol appears in the article
along with vacuum tube diode symbols. Regardless of the symbols used, this is still
a useful introduction to digital logic. Although this "Algebra in Electronic Design"
article in the February 1952 issue of Radio-Electronics magazine does not
claim to be the second part of author Edmund Berkeley's "Light Sensitive Electronic
Beast" article from the previous December's issue, it does help to know that the
"Squee" mentioned here came from there. Squee is a Robot Squirrel which has four
sensing organs, three acting organs, and a small electronic and relay brain. "Although
Squee is not a very clever robot, he does have a small amount of memory and of reasoning
ability." Boolean logic (aka Boolean algrbra), a common part of modern electronic
circuits and systems, was a relatively new concept only recently adopted from the
field of theoretical mathematics for use in digital computers. Applications were
basic AND, OR, and NOT "gates" comprised of discrete diodes (and vacuum tubes at
that) since transistors and solid state diodes had only been commercially available
for a couple years. In fact, solid state diode schematic symbol appears in the article
along with vacuum tube diode symbols. Regardless of the symbols used, this is still
a useful introduction to digital logic.
Algebra in Electronic Design

Fig. 1 - Basic switch or relay, circuit relations expressing
Boolean algebra.
By Edmund C. Berkeley
In our previous article, "Light Sensitive Electronic Beast," we talked about
Squee and about Boolean algebra, and introduced the ideas and rules of Boolean algebra.
We said that Boolean algebra had a number of important applications in the design
and simplification of circuits, and that it was used in the design of Squee and
proved very useful. Some of the use of Boolean algebra in the design of Squee will
be given in this article; but unfortunately there will be no space here to give
all the construction information for Squee. However, we shall be glad to try to
help any reader who wants to learn about or construct Squee (or other small robots).
What is Boolean Algebra?
In the last article we gave three interpretations of Boolean algebra: classes
of things; factors of a number such as 30; and relations of contacts of switches
or relays, as shown again in Fig. 1 here.
What are a, b, and c in Fig. 1? They are not actually contacts or wires; they
stand for states, conditions, or reports about contacts or wires. They stand for
reports such as "Current flowing" or "No current flowing." They always have just
one out of two values, such as yes or no, all or nothing, true or false, 1 or 0.
They are called binary variables, variables which have only two values. Any letter
labeling a contact or a wire has the value 1 if its contact is energized or closed
or if its wire is carrying current. It has the value 0 if its contact is open or
not energized, or if its wire is not carrying current. Contacts are always drawn
in the unenergized (double-contact relays) or open (single-contact relays) position.
This is referred to as the "not" position and is written a', b', etc.

Fig. 2 - Boolean relations in rectifiers.
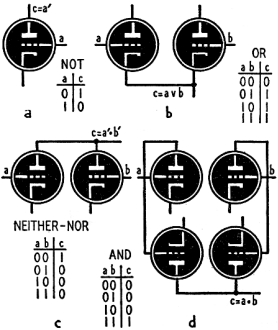
Fig. 3 - How triodes fit into the picture.
The Algebra of 1 and 0
This leads us to a fourth interpretation of Boolean algebra that is most important
for our purposes. This is the algebra of propositions or statements. Suppose that
P, Q, R stand for propositions or statements such as "Motor A is on," "Photocell
B registers light," "Relay C is energized," etc. Let T ( ... ), where the space
... is filled with a statement, stand for the "truth value of ... ," equal to 1
if the statement is true and 0 if the statement is false. Then the 1's and 0's of
truth values are a Boolean algebra.
We write T(P) = p, T(Q) = q, T (R) = r. In other words, a convenient abbreviation
for the truth value of a statement represented by a capital letter is the corresponding
small letter.
Now it can easily be shown that the following rules hold:
T (P AND Q) = p • q
T (P OR Q) = P v q = p + q - pq
T (NOT - P) = p' = 1- p
In the form of tables, we can list all the cases:

How do we convince ourselves of these tables and formulas? Let us first ask "When
is the statement P AND Q true?" Now we know from our use of AND that this is only
true if P is true (p = 1) and Q is true (q = 1). The table shows 1 for p •
q only in that case. That is what we mean by AND when we put it between statements.
By OR we ordinarily mean " ... OR ... OR BOTH." Sometimes we mean OR ELSE; but
in the connection of switch and relay contacts in parallel and often elsewhere,
the inclusive-OR is more useful than the exclusive-OR. The table above shows 1 for
p v q when one or the other or both of p and q is 1.
By NOT we mean that when P is true, NOT-P is false, and when P is false, NOT-P
is true. And this relationship the table of p and p' accurately summarizes.
As we see in the tables, we can easily write down formulas of ordinary elementary
algebra using plus, minus, times, 1, 0, which will do the same work as Boolean formulas.
In fact AND and TIMES are indistinguishable. The algebra formulas p v q = p + q
- pq and pi = 1 - p' are interesting and occasionally useful, but most of the time
the operators v (or) and ' (not) of Boolean algebra are more compact and fit more
neatly with the expression of circuits.
Interpreting Rectifiers
But there are many other types of circuit elements and other mechanisms that
have just two states, on and off, closed or open, moved to one side or moved to
the other, positioned forward or positioned back. And it is easy, logical, and efficient
to represent these two-fold conditions by Boolean algebra also. Each new type of
element leads to another interpretation of Boolean algebra.
For example, a fifth interpretation of Boolean algebra is in terms of rectifiers
(see Fig. 2). Under the term rectifiers we include vacuum tube diodes, germanium
and selenium crystal diodes, etc., any circuit element in which current flows in
one direction only.
In Fig. 2, 0 represents "low voltage" and 1 represents "high voltage." In the
OR circuit, the output line c will have a high voltage if and only if either a or
b or both have a high voltage, because then the potential drop will be all across
resistor R. In the AND circuit, the output line c will have a high voltage if and
only if both a and b are at a high voltage; for only in that case is there no drop
across the resistor.
There is no direct representation of NOT-a using rectifiers; but if the inputs
to a rectifier network include all the binary variables needed, a, b, ... , and
their individual negatives, a', b', ... , then the rectifier network can yield all
Boolean functions needed.
A good example of the use of Boolean algebra in a rectifier network to change
one set of signals into another set of signals is given in Part 12 of the series
"Constructing Electric Brains," by Berkeley and Jensen, appearing in the September,
1951, issue of Radio-Electronics, pp. 45-46.
Interpretation of Triodes

Fig. 4 - Example of how circuits can be simplified with the help
of Boolean algebra.

Fig. 5 - The sensation circuits of Squee.

Fig. 6 - Hypothetical steering circuit.

Fig. 7 - Motor circuitry.

Figs. 8 and 9 - Diagrams of light scanning and motor control
circuits in Squee.

Fig. 10 - Steering motor control circuit.
A sixth interpretation of Boolean algebra is. in terms of triodes (see Fig. 3).
Fig. 3-a is a triode with a signal a on the grid, and a signal c on the plate. If
the voltage of the grid is high (a = 1), the tube will conduct and the voltage of
the plate will be low (c = 0). If the voltage of the grid is low (a = 0), the tube
will not conduct and the voltage of the plate will be high (c = 1). The circuit
expresses c = a'.
In Fig. 3-b, we have two triodes with the cathodes connected. If the voltage
on both grids is low (a = 0, b = 0), then neither tube will conduct, and the voltage
of the cathodes will be low (c = 0). In the other three cases, the voltage of the
cathodes will be high (c = 1). The circuit expresses c = a v b.
In Fig. 3.c, we have two triodes with the plates connected. The voltage on the
plates will be high (cv= 1) if and only if the voltage on both grids is low (a =
0, b = 0). The table shows the situation. What is the equation for c?
There is a useful, general rule of Boolean algebra (which we shall call general
rule No.1) that we can use:
1. Suppose we have a complete table of 1's and 0's showing the behavior
of some binary variables.
2. Suppose y is the dependent variable and a, b, c, ... , are the
independent variables.
3. Note all the cases where y = 1.
4. If any independent variable a = 0, write a"; if any independent
variable b = 1, write b.
5. For each case, associate a', b, ... , with AND.
6. For all the cases, associate them with OR.
For example, suppose we have the following table:

Now y = 1 in two cases: case 2 where a = 0, b = 0, c = 1, and case 7 where a
= 1, b = 1, c = 0. Applying the rule, y = a' b' c v a b c'
The present instance is Fig. 3-C, and we have:
c = a' • b' = (not-a and (not-b)
In ordinary English, c here equals "neither a nor b."
How do we connect triodes to get a AND b? In Fig. 3-d, a manner of connection
is shown. The outputs of the two upper triodes have to be negated in the two lower
triodes (plate-connected) in order to give c = a • b. Obviously, therefore,
if we are using triodes and want to economize, we should prefer to work with OR
and NEITHER-NOR relations, instead of OR and AND relations.
Enough has been said, perhaps, to show that many different kinds of circuit elements
may be used to express AND, OR, NOT, EXCEPT, and other relations of Boolean algebra.
For example, pentodes could be used to represent relations of Boolean algebra. But
how can Boolean algebra simplify circuits?
Let us now take an example of a circuit and its simplification using Boolean
algebra.
Suppose we have the circuit shown in Fig. 4-b, which energizes relay Z by means
of contacts of relays W, X, and Y shown in 4-a. Our problem is to simplify this
circuit.
Looking at 4-b, we see seven (two-way) relay contacts in this circuit, and six
wire connections. This makes a total of thirteen events that modify information
carried in the wires of the circuit. Wherever there is an event of this type, the
effect on the information is a Boolean algebra operation, as may be seen in the
isolated examples shown in Fig. 4-d, 4-e, and 4-f. In either the forking contact
of 4-d or the associating contact of 4-e, change in the position of the armature
may change the information in the output. In the junction of Fig. 4-f, changing
the input from one conductor to the other is the "event" which changes the information
in the output.
So we go back to 4-b, and draw blue lines across the circuit, in such a way as
to isolate each event, from No.1 to No. 13. Now we go down through the circuit,
calculating the information which is in each wire of the network. Event 1 is the
contact w; hence the right-hand output wire contains w (contact actuated), and the
left-hand one not-w, or w' (contact not actuated). Event 2 is the contact x. Hence
the right-hand output wire contains wx and the left-hand one wx'. Event 3 is a join.
Hence the output wire contains W' v wx', which reduces to w' v x', by Boolean algebra.
This modifies the information in the incoming wires, but in this present type of
case, where we want to calculate what information energizes the relay W at the bottom
of the diagram, it is not necessary to go back and modify the descriptions of information
in the earlier wires. There are however circuits where this step is necessary -
this is the problem of "back-circuits."
And so we may go through the whole network, at each event computing the information
in each output wire, and finally after event 13 reach the wire which energizes relay
Z. The expression for the information in this wire is
w' y v wxy' v x' v wxy
which simplifies into
w v x' v y.
This expression of course represents a very simple circuit, of three contacts
in parallel, and is shown in Fig. 4-c. The circuit of 4-b (provided the contacts
have the functions expressed by the labels) reduces to the circuit of 4-c.
The process we have illustrated here is a powerful, general method, and can be
applied in many kinds of situations.
Example of Circuit Design
Boolean algebra may be used in more ways than just simplifying circuits. It may
for example be used in the design of circuits, because it can express the "yes-no"
elements in the word language describing the problem, just as well as is can express
the yes-no elements in the electrical language describing the mechanism.
For an example, let's take the problem of designing the circuits for controlling
the steering of Squee.
a. Associating Sensations and Behavior
We can work through this problem in stages. The first stage is associating the
sensations of Squee with Squee's behavior.
The sensations of Squee for steering purposes are those that are derived from
the two phototubes, the "right eye" and the "left eye." In this first stage of the
problem, we shall ignore distinctions about kind of light, a.c. or d.c. So, let
R equal the truth value of "Squee's right eye sees light," and let L equal the truth
value of "Squee's left eye sees light."
The behavior of Squee for steering purposes consists of three states: steering
clockwise, steering counterclockwise, and no steering at all. Let:
C equal the truth value of "Squee is steering clockwise,"
U equal the truth value of "Squee is steering counterclockwise," and
N equal the truth value of "Squee is not steering."
Squee must choose between these three kinds of behavior depending on Squee's
sensations. How do we associate behavior with sensations? In Fig. 5 we see the various
cases displayed; and we can see what we want to arrange. This is summarized in the
following table:

Using our general rule No.1, we have:
C = R'L' v RL' which reduces to L'
U = R'L, and
N = RL.
Translating these equations into words: Squee should steer clockwise when the
left eye does not see light; Squee should steer counterclockwise when the left eye
sees light but the right eye does not see light; and Squee should not steer at all
when both eyes see light.
Suppose that we had relays corresponding to C steering clockwise, U steering
counterclockwise, and N no steering, the schematic for the behavior of Squee would
be as in Fig. 6.
b. Associating Behavior and Action
But Squee does not have "acting organs" corresponding directly to the three states
of behavior. Instead, Squee has a steering motor, whose normal direction is such
that Squee steers clockwise, and a relay, by means of which the motor may be run
in either direction. See Fig. 7. So, let X equal the truth value of "The motor is
running" and let W equal the truth value of "The reversing relay is energized."
How do we associate actions X and W with behavior C, U, N? The logical association
is shown in the following table:
IMAGE HERE
which expresses the conditions:
(1) The motor is running if and only if C or U;
(2) The motor is reversed if U, and mayor may not be reversed if N. From this
table and general rule No.1, we obtain:
X = C v U = L v R'L = R' v L'
W = either U, or U v N = either R'L, or R'L v RL, which latter reduces to L.
Since we may use either one of the two expressions for W, we can of course use the
simpler one, W = L. The schematic circuit that corresponds to these equations is
shown in Fig. 8.
c. Taking into Account A.C. or D.C. Light, and Homing on the Nest or
Seeking Nuts
We have proceeded thus far ignoring the distinction between a.c. and d.c. light,
and whether Squee should be homing on the nest, or seeking nuts. But at this stage,
we need to take the distinction into account, and we need to translate the previously
assumed R and L sensations into appropriate sensations of a.c. and d.c. light depending
on Squee's program.
The information reported by the amplifying circuits attached to the photo-cells
is shown schematically in Fig. 9.
Four relays labeled Ra, Rb, La, Lb, are energized in the plate circuits running
from the amplifier tubes. The labels are also used for truth values:
Ra: the truth value of "The right photocell sees a.c. light";
Rb: the truth value of "The right photocell sees any light";
La: the truth value of "The left photocell sees a.c. light";
Lb: the truth value of "The left photocell sees any light."
Looking at Fig. 9, we can see that the amplifying circuit does not report directly
"the photocell sees doc. light." This information must be obtained indirectly.
The H relay shown is the "program" relay which remembers whether Squee is homing
on the nest or seeking nuts. If the "relay is energized, Squee should pay attention
only to a.c. light. If the relay is not energized, Squee should pay attention only
to d.c. light. Whether or not it is energized depends on other sensations of Squee
(the "tongue" switch, etc.) , The letter H, taken from the first letter of "homing,"
is used to label the relay and also to stand for the truth value of "Squee is homing
on the nest".
Now, how do we convert the assumed sensations R and L that we used earlier, into
the actual sensations Ra, Rb, La, Lb, with. due regard to the program H? We can
make two tables and fill in the cases according to our understanding of what is
to happen:

We can see from Fig. 9 that the case Ra equals 1 and Rb equals 0 is impossible
and so it does not have to be listed. Using general Rule 1 to summarize the table
we have:
R =Ra' Rb • H' v Ra • Rb • H
L = La' • Lb • H' v La' • Lb • H
Since Ra • Rb' is impossible, Ra is the same as Ra • Rb. Therefore,
R = Ra' • Rb • H' v Ra • H
L = La' • Lb • H' v La • H
Now,
X·= R' v L'
= (Ra' • Rb • H' v Ra • H)' v
(La' • Lb • H' v La • H)'
Using the Boolean algebra rule:
(mk v nk')' = m'k v n'k',
we have:
X = (Ra' • Rb)' • H' vV Rq' • H
v (La' • Lb)' H'
v La' • H
= (Ra v Rb') • H' v Ra' • H
v (La v Lb') • H' v La' H
= (Ra v Rb' v La v Lb') • H'
v (Ra' v La') H
Also,
W = L
= La' • Lb • H' v La • H
We now have precisely the Boolean expressions that we want, to write down a circuit
for controlling the steering of Squee. We obtain X by using four R and L contacts
in parallel, running to the negative side of an H contact, and two more Rand L contacts
in parallel running to the positive side of the same H contact. Similarly we obtain
W. See Fig. 10.
This brings us to the end of our short introduction to Boolean algebra, and its
use in the design and simplification of circuits involving "yes" and "no" elements.
We shall be glad to hear from any reader who is interested in Boolean algebra or
in the design and' construction of small robots or computers.
|





















