|
October 1931 QST
 Table of Contents Table of Contents
Wax nostalgic about and learn from the history of early electronics. See articles
from
QST, published December 1915 - present (visit ARRL
for info). All copyrights hereby acknowledged.
|
Paul Huntsinger wrote a nice introductory
article on amplitude modulation (AM) in a 1931 edition of the ARRL's QST magazine.
At the time, frequency modulation (FM) was still a laboratory curiosity, and many
"experts" believed that FM would not provide any advantage over AM broadcasting.
You might be tempted to think that sources of electrical noise that would interfere
with AM were less at the time, thus negating the need for noise-immune FM, but the
fact is by 1931 there was a lot of static caused by brushed motors, lousy automobile
ignition systems, and arcing transmission lines, along with natural sources like
lightning. Figures 6, 7, and 8 were missing in the original article, but fortunately
I was able to get them from the next month's issue of QST.
The Mechanics of Modulation

Fig. 1 - Unmodulated and modulated carrier.
By Paul R. Huntsinger*
Modulation is the process of varying the amplitude of a carrier wave in accordance
with a signal to be transmitted. For purposes of explanation it is customary to
assume that both the carrier frequency and the signaling frequency are sinusoidal
although this is not necessarily the case in practice. In discussing the qualities
of a given transmitter one usually speaks of the modulation capability of the outfit.
The modulation capability of a transmitter may be expressed either as a factor or
as a percentage, and in either case means the extent to which the amplitude of the
carrier may be varied at the signal frequency without serious distortion to the
latter.
The modulation factor is defined as the difference between the signaling and
non-signaling amplitudes of the carrier divided by the non-signaling amplitude.
Expressed as an equation,
 (1)
(1)
where M is the modulation factor. The difference between the modulated and unmodulated
carrier wave amplitudes is evidently equal to the amplitude of the signal frequency,
so we may write the above equation in the form,
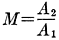 (2)
(2)
The modulation capability may be expressed as a percentage by merely multiplying
the modulation factor by 100. Fig. 1 shows a blank carrier and also one which
is modulated completely or 100%. Inspection of Equation 1 shows that for 100% modulation
the amplitude of the carrier will be twice the non-signaling value. In the ideal
case, as shown in Fig. 1, p = n = A.

Fig. 2 - Modulated power and current.
Unfortunately in practice the positive and negative peaks are not always equal
as shown in the figure, so the modulation factor p/A on the positive peaks may not
be equal to that on the negative peaks, n/A. In case the positive and negative peaks,
p and n, are unequal the modulation factor is defined as the arithmetic mean of
the positive and negative modulation factors; that is,
 (3) (3)
Inspection of the figure for the modulated wave shows that the limiting position
of the negative peaks is zero; hence the ratio n/A can never be greater than unity.
In other words the percentage of modulation on negative peaks can never be greater
than 100. If a transmitter is modulated over 100 percent the tops of the negative
peaks are cut off and the signaling frequency is seriously distorted.
Now the power of any wave varies as the square of the amplitude. Knowing the
amplitude of the modulated carrier to be 1 + M times the amplitude of the blank
carrier we may square it and find the ratio of the peak power of the modulated wave
to the blank carrier power. As an equation,
 (4) (4)

Fig. 3 - Pick-up coil.
Thus we find that in the case of 100 percent modulation the peak power will be
2 squared or four times the unmodulated carrier power. Incidentally, this shows
that for complete modulation the tube complement of the transmitter stages handling
modulated r.f. must be capable of handling power peaks four times as great as the
carrier power.
The average power of a modulated wave is found as follows: The amplitude of the
modulated carrier wave is equal to the quantity (1 +M sin qt). As was stated before,
the power of a modulated wave varies as the square of the amplitude, so the instantaneous
power may be represented by the equation,
 (5)
(5)
The average power of the modulated wave, that is the average ordinate of the
power wave, is found by integrating the power wave over a complete cycle and dividing
by 2π. Thus we find
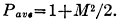 (6)
(6)
For complete modulation we have M equal to unity and so the average power is
seen to be 1 + 1/2 = 3/2 = 1.5 times the unmodulated carrier power. The power wave
is shown in Fig. 2.
Now as for the antenna or tank current of a transmitter under modulation, the
amplitude of the current will evidently be 1 + M times the unmodulated amplitude.
Since the power varies as the square of the current, the average current will necessarily
be equal to the square root of the average power. Thus we have
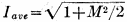 (7)
(7)
In case the modulation is complete, or 100 percent, the average power will be
1.5 times the non-signaling power and hence the antenna current will be equal to
the square-root of 1.5 or 1.226 times the unmodulated antenna current. It should
be borne in mind that this will only be the case if the modulating signal is a pure
sine wave and then only after sufficient time has elapsed for the antenna ammeter
to reach its maximum steady reading.1
Methods of Measuring Modulation Percentage
One method of measuring the modulation factor of a transmitter is by the use
of a current-squared galvanometer.2 The hook-up used is shown in Fig. 3,
the pickup coil being coupled to the tank of the output stage of the transmitter.
Two changes must be made in equation (1) before it is suitable for use in this method.
First, since the galvanometer is calibrated in current squared, it will be necessary
to take the square-root of the right hand member. Second, since the instrument reads
effective rather than peak values and since the factor is defined in terms of peak
values, we must also multiply by the square-root of 2. Making the above changes
in the equation and simplifying we have,
 (8) (8)
where D represents the deflection of the instrument under the conditions shown.
A convenient way of finding the factor is to couple the pickup coil to the tank
sufficiently so that a reading of 40 scale divisions is obtained with no modulation.
Complete or 100 percent modulation will deflect the pointer to 60. For any deflection
noted upon modulation, the factor may be computed by substituting the readings in
the equation. Here is a check upon the above method. The full-scale reading of the
instrument represents a current of 115 milliamperes. The current for any deflection
will then be,
 (9) (9)

Fig. 4 - Carrier shift waveform.
From the above equation we find the current for a deflection of 40 divisions
to be 72.773 ma. while that for 60 divisions is 89.079 ma. The ratio of the second
to the first is 1.226 which, as shown before, is the ratio of the antenna currents
for complete and zero modulation of the carrier wave. The fault in this method of
determining the factor is that nothing whatever can be told of the relative amplitudes
of the positive and negative peaks. However, the average modulation, as defined
before, can be determined very easily by this method.

Fig. 5 - Positive and negative modulation graphs.

Fig. 6 - If the curves for positive and negative peaks coincide,
the undistorted output will be maximum.

Fig. 7 - A typical oscillogram and what happens to the waveform
when 100% modulation is attempted with a transmitter having a modulation capability
of 30%.

Fig. 8 - This arrangement measures the alternating component
of the current.
The modulation factor may be determined also by means of a linear rectifier and
vacuum tube voltmeter.3 This method is used in the General Radio modulation
meter. Both positive and negative peaks may be measured as well as the resulting
carrier shift if the peaks are not equal. It is readily seen that if the positive
peaks are greater than the negative peaks the carrier power will shift upward under
modulation and vice versa as shown in Fig. 4. A transmitter should be tuned
so that the mean plate current of the modulated stage and that of the linear amplifiers
does not shift either up or down on modulation. If so tuned there will be no carrier
shift and consequently the positive and negative peaks will be equal in amplitude.
The relation between audio-frequency volts inputs to a transmitter and percentage
modulation must be linear over the working range of the transmitter if no distortion
of the modulated signal is to take place. This relation, both for positive and negative
modulation, is easily determined if one has a good audio frequency oscillator and
level indicator. The ideal case is shown in Fig. 5A while a possible relation
is shown in Fig. 5B. The negative peaks drop off slightly, hence there will
be some carrier shift upward at this level. This falling off of the negative peaks
is due to curvature in the lower end of the dynamic characteristic of the tubes.
A transmitter should be adjusted so that there is no carrier shift in modulation
and then the curves for both positive and negative peaks will coincide. If this
is done practically the only distortion encountered will be a slight flattening
of the tops of the wave at high modulation levels. If the curve for negative peaks
is swung around we have the modulation characteristic of the entire transmitter.
By assuming a sine wave input to the transmitter and plotting the output wave as
shown in Fig. 6 we may analyze it for harmonic distortion. If the curves for
positive and negative peaks coincide, the transmitter operating point is midway
between the upper and lower bends in the dynamic characteristic of the tubes and
the undistorted output will be a maximum.
The oscillograph is the best method for checking the operation of a transmitter
since it will show the waveform of the output as well as the value of the peaks.
A typical oscillogram is shown in Fig. 7A and was obtained by exciting the
oscillograph element from the output of a linear rectifier which was coupled to
the tank circuit. Fig. 7B shows what happens to the waveform of a signal when
one tries to modulate 100% a transmitter having but 30% modulation capability. The
cutting off of the positive halves of the cycle is caused by the modulator grid
going positive.
Still another method of measuring the percentage of modulation is shown in Fig. 8.
A resistor of proper size is connected in the plate supply lead to the modulated
tube. The alternating-current voltage drop in the resistor is rectified by a copper-oxide
rectifier which drives a direct current microammeter. The direct current component
of the plate current is kept out of the rectifier by the blocking condenser C whose
impedance is low at audio frequency. The resistor is made of such size that the
instrument reads full scale when the alternating-current component of the plate
current is equal to the direct current component, which is the condition for 100%
modulation. Another form of the instrument uses a current transformer and alternating-current
ammeter. This type is inferior to the first mentioned since the scale of the instrument
is not linear and the damping is necessarily high, the last mentioned preventing
the instrument from following the peaks.
* WOI. Iowa State College, Ames, Iowa.
1. The increase in antenna current as indicated by the r.f. ammeter
will be 22.6% only when the modulating signal is sinusoidal. Complex modulation
frequencies such as those caused by speech or music will give an antenna current
increase of greater than 22.6% for amplitude modulation of 100%. - Editor.
2. See also Experimenters' Section, May, 1930; and "The Neglected
Current-Squared Galvanometer," Feb., 1931. - Editor.
3. This method is used in the modulometer, described in QST,
Aug., 1929. Positive or negative peaks may be measured by reversing the input connections
to the grid circuit of the voltmeter tube. - Editor.
Posted March 29, 2022
(updated from original post on 6/22/2016)
|






 (1)
(1) 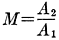 (2)
(2) 
 (3)
(3)
 (4)
(4)

 (5)
(5) 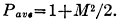 (6)
(6) 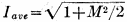 (7)
(7)  (8)
(8)
 (9)
(9)








