|
September 1975 Popular Electronics
 Table of Contents Table of Contents
Wax nostalgic about and learn from the history of early electronics. See articles
from
Popular Electronics,
published October 1954 - April 1985. All copyrights are hereby acknowledged.
|
With the high
degree of computer automation at this point in time, it is doubtful that many
people still bother to perform digital logic simplification manually by using a
Karnaugh Map. Online apps like this one (KarnaughMapSolver.com)
do all the heavy lifting for you, producing minterms, maxterms, a truth table,
and a written-out Boolean expression. Back in the late 1980s when I was working
on my BSEE at UVM, the Karnaugh Map, created by Maurice Karnaugh,
of Bell Labs, was introduced in a digital electronics course. It was a fairly
easy concept to grasp. Is it taught in electronics curricula these days? This
1975 Popular Electronics magazine article provides a great introduction
to the Karnaugh Map. It appeared during the era where large scale integrated (LSI)
microcircuits were being widely designed into all forms of electronic products.
Karnaugh Maps for Fast Digital Design
 By Art Davis By Art Davis
Have you ever tackled a digital design project with vim and vigor-only to find
yourself entangled in a morass of logic ones and zeros and a "this goes up, and
that goes down" nightmare? If you have, don't despair. There is a much neater, much
simpler method than the brute force approach. This article provides a coherent approach
to digital design. The method Is not a substitute for intuition and practical seat-of- the-pants experimentation, but a tool for getting the end results quickly.
Before getting down to actual techniques, it might be wise to do a little reviewing.
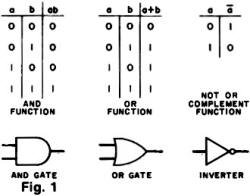
The truth tables for the AND, OR, and NOT (or COMPLEMENT, or INVERTER) functions
are shown in Fig. 1. The function a AND b is written ab; a OR b is written
a + b;
and NOT a is written a. Note that + as defined here is different from ordinary addition,
and merely symbolizes the function defined by the truth table of Fig. 1. A truth
table is simply an array, one side of which contains all possible combinations of
the input variables and the other side of which contains the corresponding values
of a logic function or output. Figure 1 also shows the digital logic gate symbols
for the three functions.
 Any logic function can be constructed from these three
basic types of functions or gates. It is often convenient, though, when working
with a particular type of logic family (TTL, DTL, etc.) to use two other types of
function, the NAND and the NOR. The NAND function of a and b is written ab, and
the NOR function, a + b. Their truth tables and logic symbols are illustrated in
Fig. 2. All of these functions except the NOT, or INVERTER, can be extended in an
obvious way to include more than two inputs. With these functions at hand, it becomes
possible to construct any logic function desired. Any logic function can be constructed from these three
basic types of functions or gates. It is often convenient, though, when working
with a particular type of logic family (TTL, DTL, etc.) to use two other types of
function, the NAND and the NOR. The NAND function of a and b is written ab, and
the NOR function, a + b. Their truth tables and logic symbols are illustrated in
Fig. 2. All of these functions except the NOT, or INVERTER, can be extended in an
obvious way to include more than two inputs. With these functions at hand, it becomes
possible to construct any logic function desired.
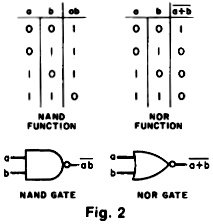
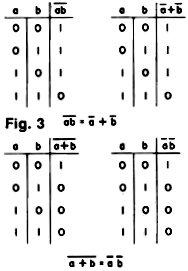
In manipulating the basic functions
to form more complex ones, it is expedient to have available two important, yet
simple, rules of basic logic theory known as DeMorgan's Laws. Figure 3 contains
truth tables for the logic functions ab,
a + b, a + b, and
a-b. Comparing them yields the formulas of DeMorgan's
Laws:
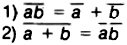
These formulas are useful in implementing digital functions using only NAND
or only NOR gates.
Why Map Techniques?
 A truth table is one way of specifying a logic function - the Karnaugh map
(pronounced Kar-no) is another. To get an idea of what such a map is, and why it
is a convenient tool, let's look at a practical digital design problem. A truth table is one way of specifying a logic function - the Karnaugh map
(pronounced Kar-no) is another. To get an idea of what such a map is, and why it
is a convenient tool, let's look at a practical digital design problem.
Suppose we are faced with designing the digital black box of Fig. 4, which
has three inputs a, b and c, and a single output f(a,b,c). The black box is to
provide a logic one output under the following input conditions:
a=b=c=1, a=c=1 and b=0, a=0 and b=c=1, or a=b=0 and c=1. How can we
manufacture the digital logic inside the box from this specification?
One possible answer is to be methodical. A person unfamiliar with map
techniques - but very methodical - might reason in the following way.
"The output function f(a,b,c) is logic one whenever a=b=c=1. An AND gate puts
out a one whenever all inputs are logic one, so let's use an AND. But the AND
output is zero for all other input combinations, and f(a,b,c) is a one for
several other input conditions.
"Well, the AND gate did pretty well for the first input combination, so why
not try it for the second? Let's take the complement of b by passing it through
an INVERTER and run it into an AND gate with a and c. This AND will put out a
one when a=c=1 and b=0, as desired. This seems to be working well, so let's do
the same with each of the other two combinations."
 With all the AND gates and INVERTERs arranged as above, our methodical
experimenter will then observe that, since f(a,b,c) is to be a logic one
whenever the input variables form the first combination, or the second, or the
third, or the fourth, all he has to do is OR the outputs of the four ANDs to
generate f(a,b,c). The resulting logic is shown in Fig. 5. With all the AND gates and INVERTERs arranged as above, our methodical
experimenter will then observe that, since f(a,b,c) is to be a logic one
whenever the input variables form the first combination, or the second, or the
third, or the fourth, all he has to do is OR the outputs of the four ANDs to
generate f(a,b,c). The resulting logic is shown in Fig. 5.
Now this logic design works. It will do the digital job, but it is
inefficient. It requires four AND gates, one OR, and two INVERTERs. This is
costly, and it would cause quite a few layout problems because of the numerous
interconnections. In addition, the design procedure outlined above is slow and,
for more complicated circuits, error prone. What can be done to 'streamline the
procedure?
The answer is the Karnaugh map. This is just a rectangle divided up into a
number of squares, each square corresponding to a given input combination. The
Karnaugh map of our function f(a,b,c) is shown in Fig. 6. The right half of the
map corresponds to a=1, the left half to a=0 (a=1), the middle half to b=1, and so
on. The basic idea is that there is one square for each input combination. If we
write into that square the value of the output function for that particular
input combination, we will have completely specified the function. The ones and
zeros in Fig. 6 are the values which f(a,b,c) assumes for the associated input
variable combinations.
 Now recalling our methodical design procedure, it is easy to see that each
square which has a one in it corresponds to the AND function of those input
variables, and f(a,b,c) can be generated as the OR function of all of the ANDs. Now recalling our methodical design procedure, it is easy to see that each
square which has a one in it corresponds to the AND function of those input
variables, and f(a,b,c) can be generated as the OR function of all of the ANDs.
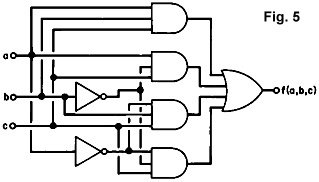 A key factor arises here. It isn't necessary to include all of these AND
functions, and the Karnaugh map tells us how to eliminate some of the terms. For
example, looking at Fig. 6, we see that f(a,b,c) is a one for four adjacent
boxes forming the bottom half of the map. (We will consider squares on opposite
edges to be adjacent.) It is also easy to see the following: The only variable
which does not change as we go from one square with a one to another with a one
is c. It remains at one. What this means is that f(a,b,c) cannot depend on a and
b because, regardless of their values, f(a,b,c) is a one as long as c=1.
Therefore we can forget about a and b, and implement our black box as shown in
Fig. 7. We have grouped together the four adjacent squares to eliminate a and b.
Notice that we have simplified things a great deal, since we now need no gates
at all. A key factor arises here. It isn't necessary to include all of these AND
functions, and the Karnaugh map tells us how to eliminate some of the terms. For
example, looking at Fig. 6, we see that f(a,b,c) is a one for four adjacent
boxes forming the bottom half of the map. (We will consider squares on opposite
edges to be adjacent.) It is also easy to see the following: The only variable
which does not change as we go from one square with a one to another with a one
is c. It remains at one. What this means is that f(a,b,c) cannot depend on a and
b because, regardless of their values, f(a,b,c) is a one as long as c=1.
Therefore we can forget about a and b, and implement our black box as shown in
Fig. 7. We have grouped together the four adjacent squares to eliminate a and b.
Notice that we have simplified things a great deal, since we now need no gates
at all.
Using a Karnaugh Map
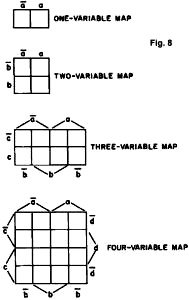
  Maps of one, two, three, and four variables are shown in Fig. 8. Maps of one
variable are rarely used, and maps with more than four variables are seldom
needed - even if such a problem were to chance along, the Karnaugh map would not
be the tool to use. Its value depends on the pattern recognition capability of
the user, and it becomes hard to recognize pattern groupings in maps of more
than four variables. Maps of one, two, three, and four variables are shown in Fig. 8. Maps of one
variable are rarely used, and maps with more than four variables are seldom
needed - even if such a problem were to chance along, the Karnaugh map would not
be the tool to use. Its value depends on the pattern recognition capability of
the user, and it becomes hard to recognize pattern groupings in maps of more
than four variables.
Using the three-variable map as an example, note that there is one box for
abc, one for abc, another for
abc, and so on, with abc corresponding to
the input combination a=1, b=1, c=1; abc
to a=1, b=0, c=1; and abc to a =0, b =1, c =0; etc. Each box,
then, corresponds to a single row in the truth table. The map is arranged in
such a way that half of it corresponds to the uncomplemented form of a given
variable and the other half to its complemented form; and the variables are
interleaved so that every input combination corresponds to exactly one square,
and conversely. Usually only the uncomplemented form of each variable is written
- it being clear that the other hall of the map corresponds to the complemented
form.
 Now, a logic function is displayed by placing ones and zeros in the boxes on
the map. If a given input combination produces an output, or function value, of
one, a one is placed in the corresponding square on the map. If the output is
zero, a zero is placed in the square. As an example, look at the logic function
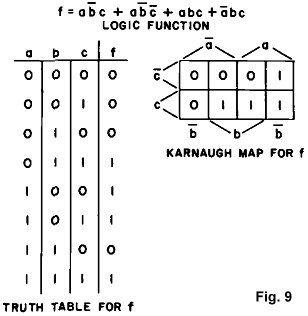
in Fig. 9. On the Karnaugh map, the box given by abc has a 1 in it. This means
that f is a logical one when the input variables have the value a=1, b=1, and
c=1. The box given by abc has a 0
in it. This means that f=0 when a=1, b=1, and c=0. These entries, as well as all
the others, can be verified by looking at the truth table. Now, a logic function is displayed by placing ones and zeros in the boxes on
the map. If a given input combination produces an output, or function value, of
one, a one is placed in the corresponding square on the map. If the output is
zero, a zero is placed in the square. As an example, look at the logic function
in Fig. 9. On the Karnaugh map, the box given by abc has a 1 in it. This means
that f is a logical one when the input variables have the value a=1, b=1, and
c=1. The box given by abc has a 0
in it. This means that f=0 when a=1, b=1, and c=0. These entries, as well as all
the others, can be verified by looking at the truth table.
The logic function in Fig. 9 is not at all simple looking. The question is,
how can the function be reduced to its simplest form? Variables can be
eliminated from the function by use of the following definition and rules:
Definition: Two boxes are adjacent if the corresponding
variables differ in only one place, for example if one box corresponds to a b c and the other to abc. Notice that
boxes on opposite edges of the map are adjacent under this definition.
Rule 1:
If two boxes containing ones are adjacent, the single variable which differs
between the two (uncomplemented for one, complemented for the other) can be
eliminated and the two boxes combined. These two boxes correspond to the AND
function of all the variables except the one eliminated.
Rule 2: If four boxes
containing ones are adjacent in such a way that each box is adjacent to at least
two others, these boxes can be combined and the two variables eliminated-those
two which appear in both complemented and uncomplemented form somewhere within
the group. The group of four corresponds to the AND function of all the
variables except for the two which have been eliminated.
 Rule 3: The same
procedure holds for eight, sixteen, and so on, adjacent boxes. Each box in a
grouping must be adjacent to three, four, etc., others within that group. Rule 3: The same
procedure holds for eight, sixteen, and so on, adjacent boxes. Each box in a
grouping must be adjacent to three, four, etc., others within that group.
Rule
4: The various AND functions produced by the above groupings are "ORed" together
to yield the simplest function.
It should be noted that a given box can be
included in more than one grouping if that will simplify the overall function,
but each grouping should contain at least one box which doesn't belong to an
existing grouping (otherwise, this would lead to redundancy).
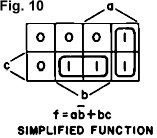
 To illustrate, the Karnaugh map of Fig. 9 is repeated in Fig. 10, along with
the adjacency groupings and the resulting simplified function. Note the contrast
in simplicity. The boxes represented by abc and abc, although adjacent, are not grouped
together because each is already included in an existing grouping. Now we are
equipped to tackle a real -life problem. To illustrate, the Karnaugh map of Fig. 9 is repeated in Fig. 10, along with
the adjacency groupings and the resulting simplified function. Note the contrast
in simplicity. The boxes represented by abc and abc, although adjacent, are not grouped
together because each is already included in an existing grouping. Now we are
equipped to tackle a real -life problem.
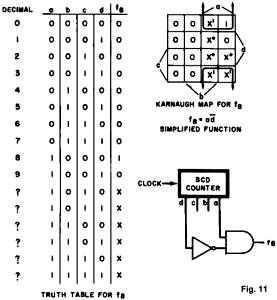
BCD-to-Decimal Decoder
Consider the BCD counter of Fig. 11, with the four output variables a, b, c,
and d. Suppose we need to decode the count of decimal eight and provide a
control pulse, lasting one clock period, to some other digital circuit. We must
build a logic function defined by the truth table of Fig. 11. This truth table
introduces a new variable, called a don't care and given the symbol "X" The
don't care means that we can define the output function f to be either zero or
one for that particular input combination-simply because the input combination
will never occur. A BCD counter never counts above decimal nine. The X's can be
given values of zero or one so as to simplify the resulting function. In our
case, the don't cares have been chosen as indicated by the smaller ones and
zeros on the map. Notice the very simple form for the function f8, which can be
constructed from a single AND gate and an INVERTER.
The preceding was an example of what is called combinational logic. The
outputs at a given time are dependent only upon the inputs at that time.
Actually, the gates used to build up a logic function have some delay. In the
case of combinational logic, though, this just means that after the input values
are established, there is some flat delay before the output value is
established. The delay is critical only if we have to compare the output value
with another being similarly generated. If this is the case, we could encounter
problems with the timing margins.
 In the digital game we are playing, though, the gate delays can be important
for a different reason. They allow us to build so-called sequential machines for
storing information, as well as for a myriad of other useful things. The general
idea of a sequential machine is illustrated in Fig. 12. All the gate delays of
delta seconds - for illustrative purposes only-are assumed to be lumped into the
output leads. The leads labeled x1, x2 and x3 are the external inputs, and those
tagged q1, q2, and q3 are the outputs. (There
could, of course, be any number of inputs and any number of outputs.) The leads
labeled Q1, Q2, and Q3, are assumed to respond
instantaneously to the inputs and fed-back outputs. In the digital game we are playing, though, the gate delays can be important
for a different reason. They allow us to build so-called sequential machines for
storing information, as well as for a myriad of other useful things. The general
idea of a sequential machine is illustrated in Fig. 12. All the gate delays of
delta seconds - for illustrative purposes only-are assumed to be lumped into the
output leads. The leads labeled x1, x2 and x3 are the external inputs, and those
tagged q1, q2, and q3 are the outputs. (There
could, of course, be any number of inputs and any number of outputs.) The leads
labeled Q1, Q2, and Q3, are assumed to respond
instantaneously to the inputs and fed-back outputs.
If the inputs have been in one state for a long time, the circuit will have
settled into a stable situation with q1, q2, and q3 identical with
Q1, Q2, and Q3, respectively. Now suppose one or more of the inputs changes values. Then no
longer will the small q's be the same as the upper-case Q's. After the passage
of (delta) time corresponding to the gate delays, though, the values of Q will
have propagated through to the outputs, and the small q's will again be
identical with the large ones. For a given set of input values, then, the small
q's are called the unstable states and the large ones the stable states of the
sequential machine. The feature which allows memory storage and other effects is
the regenerative characteristics created by the feedback.
The R-S Flip-Flop
An R-S flip-flop is a one-bit digital memory whose output is set to the one
state by a one on an input set (S) line and to the zero state by a one on
another line, called the reset (R). An incomplete truth table for this device is
sketched in Fig. 13. It is incomplete because the output stable state is
specified not only in terms of ones, zeros, and don't cares, but depends in
addition on the present (unstable) state q. We can form a complete truth table
by including q as one of the input variables, thus creating a feedback
situation. The complete truth table is also shown in Fig. 13, along with the
resulting Karnaugh map and the derived logic equation for the state Q. Note that
we must always have RS=0 (called the RS flip-flop constraint) to keep from
violating the condition that R=S=1 must never occur. Figure 13 also shows how
DeMorgan's Law is used to get the function into a form requiring only NOR gates
for its construction. By assuming all three possible combinations of input
variables (remembering the R=S=1 is disallowed from ever occurring) and
computing outputs, the truth table can easily be verified. It is also easy to
show in this way that the output labeled
Q is, indeed, the complement of the output labeled Q for all input
conditions except the disallowed R=S=1.
The Clocked R-S Master-Slave Flip-Flop
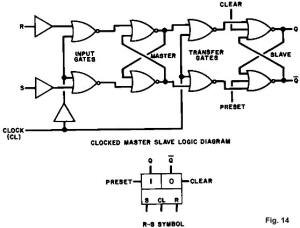 It is often desirable to have available an R -S flip-flop which changes state
only on, for example, the trailing edge (or 1-0 transition) of a clock signal.
It is possible to use the Karnaugh map to derive the form of such a flip-flop,
but the end result, although economical in number of gates and number of inputs
per gate, would not shed much light on the internal workings. It is often desirable to have available an R -S flip-flop which changes state
only on, for example, the trailing edge (or 1-0 transition) of a clock signal.
It is possible to use the Karnaugh map to derive the form of such a flip-flop,
but the end result, although economical in number of gates and number of inputs
per gate, would not shed much light on the internal workings.
This type of sequential machine is depicted in Fig. 14. When the clock goes
high, the R and S inputs are passed through the input gates and stored in the
master. When the clock goes low, the input gates are disabled, and the
information is coupled through the transfer gates into the slave flip-flop. The
function of the preset and clear inputs is evident. Try assuming a set of input
values for R and S, and trace the information flow, letting the clock change as
described above, to convince yourself that the unit performs the R-S function.
The J-K Flip-Flop
 Let's return to our newly developed map technique now and develop the
(clocked) J-K flip-flop as a last example. For convenience, since output changes
are allowed only on clock transitions, let's denote the unstable state q by Qn
and the stable state Q by Qn+1. This is reasonable, because Qn
is the stable state just prior to the nth 1-0 clock transition, and is the
unstable state just afterward, with the flip-flop settling down into the stable
state Qn+1 before the next clock transition occurs. Let's return to our newly developed map technique now and develop the
(clocked) J-K flip-flop as a last example. For convenience, since output changes
are allowed only on clock transitions, let's denote the unstable state q by Qn
and the stable state Q by Qn+1. This is reasonable, because Qn
is the stable state just prior to the nth 1-0 clock transition, and is the
unstable state just afterward, with the flip-flop settling down into the stable
state Qn+1 before the next clock transition occurs.
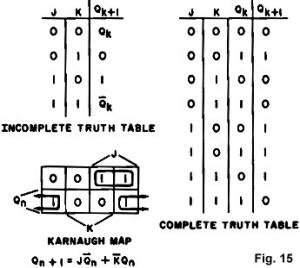 The incomplete and complete truth tables are shown in Fig. 15, along with the
Karnaugh map and the resulting simplified function. The J serves as the S and K
as the R, respectively, of an R -S flip-flop. The only difference is that the
J=K=1 output is now defined (Qn). The incomplete and complete truth tables are shown in Fig. 15, along with the
Karnaugh map and the resulting simplified function. The J serves as the S and K
as the R, respectively, of an R -S flip-flop. The only difference is that the
J=K=1 output is now defined (Qn).
Let's use the clocked R-S flip-flop to build the J-K from our derived
equation. For this purpose, let S=JQn
and R=KQn be the
inputs to the clocked R-S. According to the R-S equation,
Qn+1 = S + RQn
= JQn + (KQn)Qn
Now, applying DeMorgan's law to KQn,
we get
Qn+1 = JQn
+ (K + Qn)Qn = JQn +
KQn + QnQn.
But QnQn
= 0 always, so
Qn+1 = JQn
+
KQn
which is the J-K flip-flop equation.
Notice that the R-S constraint is satisfied, since
RS = (JQn)(KQn)
= JK(QnQn)
= 0
Fig. 16 shows the construction of the J-K from the R-S using two AND gates.
Again, test the operation by assuming a set of conditions for J and K
and tracing the logic flow. A glance back at the incomplete truth table will
reveal that if J=K=1 (J and K inputs tied to a logic one) the J-K forms a
toggle flip-flop.
The preceding examples have been intended to accomplish two things. In the
first place, knowledge of the logical operation of the various types of
flip-flops is essential in order to use them intelligently in an original
design. As a second objective, they have provided an effective demonstration of
the economy of thought which results when the Karnaugh may is used in a digital
design effort.
|





 By Art Davis
By Art Davis
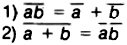
 A truth table is one way of specifying a logic function - the Karnaugh map
(pronounced Kar-no) is another. To get an idea of what such a map is, and why it
is a convenient tool, let's look at a practical digital design problem.
A truth table is one way of specifying a logic function - the Karnaugh map
(pronounced Kar-no) is another. To get an idea of what such a map is, and why it
is a convenient tool, let's look at a practical digital design problem.  With all the AND gates and INVERTERs arranged as above, our methodical
experimenter will then observe that, since f(a,b,c) is to be a logic one
whenever the input variables form the first combination, or the second, or the
third, or the fourth, all he has to do is OR the outputs of the four ANDs to
generate f(a,b,c). The resulting logic is shown in Fig. 5.
With all the AND gates and INVERTERs arranged as above, our methodical
experimenter will then observe that, since f(a,b,c) is to be a logic one
whenever the input variables form the first combination, or the second, or the
third, or the fourth, all he has to do is OR the outputs of the four ANDs to
generate f(a,b,c). The resulting logic is shown in Fig. 5.  Now recalling our methodical design procedure, it is easy to see that each
square which has a one in it corresponds to the AND function of those input
variables, and f(a,b,c) can be generated as the OR function of all of the ANDs.
Now recalling our methodical design procedure, it is easy to see that each
square which has a one in it corresponds to the AND function of those input
variables, and f(a,b,c) can be generated as the OR function of all of the ANDs.  A key factor arises here. It isn't necessary to include all of these AND
functions, and the Karnaugh map tells us how to eliminate some of the terms. For
example, looking at Fig. 6, we see that f(a,b,c) is a one for four adjacent
boxes forming the bottom half of the map. (We will consider squares on opposite
edges to be adjacent.) It is also easy to see the following: The only variable
which does not change as we go from one square with a one to another with a one
is c. It remains at one. What this means is that f(a,b,c) cannot depend on a and
b because, regardless of their values, f(a,b,c) is a one as long as c=1.
Therefore we can forget about a and b, and implement our black box as shown in
Fig. 7. We have grouped together the four adjacent squares to eliminate a and b.
Notice that we have simplified things a great deal, since we now need no gates
at all.
A key factor arises here. It isn't necessary to include all of these AND
functions, and the Karnaugh map tells us how to eliminate some of the terms. For
example, looking at Fig. 6, we see that f(a,b,c) is a one for four adjacent
boxes forming the bottom half of the map. (We will consider squares on opposite
edges to be adjacent.) It is also easy to see the following: The only variable
which does not change as we go from one square with a one to another with a one
is c. It remains at one. What this means is that f(a,b,c) cannot depend on a and
b because, regardless of their values, f(a,b,c) is a one as long as c=1.
Therefore we can forget about a and b, and implement our black box as shown in
Fig. 7. We have grouped together the four adjacent squares to eliminate a and b.
Notice that we have simplified things a great deal, since we now need no gates
at all. 
 Maps of one, two, three, and four variables are shown in Fig. 8. Maps of one
variable are rarely used, and maps with more than four variables are seldom
needed - even if such a problem were to chance along, the Karnaugh map would not
be the tool to use. Its value depends on the pattern recognition capability of
the user, and it becomes hard to recognize pattern groupings in maps of more
than four variables.
Maps of one, two, three, and four variables are shown in Fig. 8. Maps of one
variable are rarely used, and maps with more than four variables are seldom
needed - even if such a problem were to chance along, the Karnaugh map would not
be the tool to use. Its value depends on the pattern recognition capability of
the user, and it becomes hard to recognize pattern groupings in maps of more
than four variables. 
 Rule 3: The same
procedure holds for eight, sixteen, and so on, adjacent boxes. Each box in a
grouping must be adjacent to three, four, etc., others within that group.
Rule 3: The same
procedure holds for eight, sixteen, and so on, adjacent boxes. Each box in a
grouping must be adjacent to three, four, etc., others within that group.  To illustrate, the Karnaugh map of Fig. 9 is repeated in Fig. 10, along with
the adjacency groupings and the resulting simplified function. Note the contrast
in simplicity. The boxes represented by abc and a
To illustrate, the Karnaugh map of Fig. 9 is repeated in Fig. 10, along with
the adjacency groupings and the resulting simplified function. Note the contrast
in simplicity. The boxes represented by abc and a

 Let's return to our newly developed map technique now and develop the
(clocked) J-K flip-flop as a last example. For convenience, since output changes
are allowed only on clock transitions, let's denote the unstable state q by Qn
and the stable state Q by Qn+1. This is reasonable, because Qn
is the stable state just prior to the nth 1-0 clock transition, and is the
unstable state just afterward, with the flip-flop settling down into the stable
state Qn+1 before the next clock transition occurs.
Let's return to our newly developed map technique now and develop the
(clocked) J-K flip-flop as a last example. For convenience, since output changes
are allowed only on clock transitions, let's denote the unstable state q by Qn
and the stable state Q by Qn+1. This is reasonable, because Qn
is the stable state just prior to the nth 1-0 clock transition, and is the
unstable state just afterward, with the flip-flop settling down into the stable
state Qn+1 before the next clock transition occurs.



