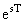|
In mathematics, the
Laplace transform is one of the best known and most widely used integral transforms.
It is commonly used to produce an easily solvable algebraic equation from an ordinary
differential equation. It has many important applications in mathematics, physics,
optics, electrical engineering, control engineering, signal processing, and probability
theory.
In mathematics [and engineering], it is used for solving differential and integral
equations. In physics and engineering, it is used for analysis of linear time-invariant
systems such as electrical circuits, harmonic oscillators, optical devices, and
mechanical systems. In this analysis, the Laplace transform is often interpreted
as a transformation from the time-domain, in which inputs and outputs are functions
of time, to the frequency-domain, where the same inputs and outputs are functions
of complex angular frequency, in radians per unit time. Given a simple mathematical
or functional description of an input or output to a system, the Laplace transform
provides an alternative functional description that often simplifies the process
of analyzing the behavior of the system, or in synthesizing a new system based on
a set of specifications. - Wikipedia
See also LaPlace Transform
Properties
 |
↔ |
 |
 |
↔ |
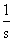 |
 |
↔ |
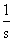 |
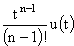 |
↔ |
 |
 |
↔ |
 |
 |
↔ |
 |
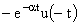 |
↔ |
 |
 |
↔ |
 |
 |
↔ |
 |
| |
|
|
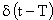 |
↔ |
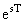 |
 |
↔ |
 |
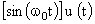 |
↔ |
 |
 |
↔ |
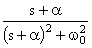 |
 |
↔ |
 |
|