The Oscilloscope as a Resonance and LC Tester
February 1960 Electronics World

February 1960 Electronics World   Table of Contents  Wax nostalgic about and learn from the history of early electronics. See articles from Electronics World, published May 1959 - December 1971. All copyrights hereby acknowledged.

All of the oscilloscope measurement techniques presented in this 1960 Electronics World magazine article apply to 2018 circuit measurements. Anyone who attended a high school or college electronics lab has created and measured capacitance, inductance and resonance using an o-scope as part of a classroom exercise. We all were wowed the first time we hooked up signal generators to both the horizontal and vertical deflection inputs and observed rotating Lissajous patterns on the display. Don't tell me you didn't twist the frequency and amplitude knobs of the sig gens with the delight of a kid playing with an Etch-A-Sketch. When I was taking labs in the 1970's and 1980's, school oscilloscopes were all analog and had no handy-dandy digital readout marker functions that helped make rise time and fall time measurements a little easier. We used the X- and Y- trace position adjuster knobs to move the waveform to a convenient measurement point behind the etched display grid, and then counted whole squares and interpolated between them. The same applied to spectrum analyzers. There was undeniably a benefit to learning the skill, but I definitely appreciate modern test equipment with digital markers and math functions.

The Scope as a Resonance and LC Tester

By A. A. Mangieri

Test flybacks, check resonance, measure inductance or capacitance with two resistors and your scope.

The modern oscilloscope is regarded by many as the most versatile of test instruments. Few people claim to know all the uses to which it may be put. New uses are always being suggested. The possibility of measuring resonance with the oscilloscope was investigated because a convenient method of checking low-frequency tanks, in the range of 1 to 200 kilocycles, was needed. Popular devices normally used to measure resonant frequencies, like grid-dip meters, do not generally extend below 300 kc. As for unknown values of an inductance or capacitance, they can be found by resonating them against known components.

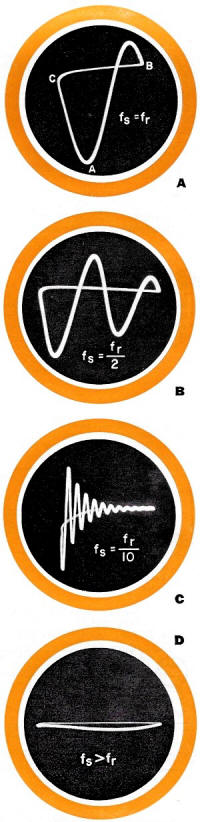
Fig. 1. Oscilloscope displays obtained (A) when sweep rate (f_s) and resonant. frequency of the tank (f_r) are equal, (B, C) when f_s is a subharmonic of f_r, and (D) when f_s is greater than f_r.

The method worked out was that of exciting a parallel connection of L and a with the saw-tooth output from an oscilloscope. Circuit connections for the technique are shown in Fig. 2. The saw-tooth voltage (E₁) is applied to the LC network and an output voltage (E₂) is taken from the tank for application to the vertical input of the oscilloscope. Isolation resistors R₁ and R₂ are not critical: values anywhere from 50,000 to 250,000 ohms are satisfactory.

Theory of Operation

A saw-tooth wave is an excellent source of a broad band of frequencies. In addition to its fundamental, it contains a sequence of usable odd and even harmonics of progressively smaller amplitude. The parallel LC circuit will exhibit a characteristically high impedance at its single frequency of resonance.

We may understand behavior of the circuit if we first think of the saw-tooth wave, E₁ as a pulse that shock-excites the tank circuit. This results in a damped, transient oscillation, E₂. The frequency of oscillation is determined by the LC tank and the damping by the "Q" of the circuit.

We will call the fundamental sweep frequency or repetition rate of the saw-tooth waveform f_s and the resonant frequency of the LC circuit f_r. If the sweep-frequency controls of the scope are adjusted so that these two are equal (f_s = f_r), the oscilloscope pattern will resemble Fig. 1A, displaying one cycle of oscillation. If the sweep frequency is one-half the resonant LC frequency (f_s = f_r/2), a two-cycle display (Fig. 1B) results, with the second cycle smaller in amplitude than the first. With f_s much lower than f_r (f_s = f_r/10), the damped oscillation of Fig. 1C results. If the sweep frequency should differ from the resonant frequency in the other direction - that is, if f_s should be greater than f_r, the waveform collapses as shown in Fig. 1D.

If f_r is unknown, how can we determine when sweep frequency f_s is correctly set to it? This is done simply by adjusting the sweep frequency while observing point A in Fig. 1A. This point will extend and retract vertically as we sweep through the resonant frequency. The point of maximum extension (maximum pattern height) occurs when f_s = f_r. Similarly, when we sweep f_s gradually through f_r/2, point A exhibits like behavior, but with reduced amplitude. During normal adjustment, point A will also seem to move from side to side, and the retrace line (B-C) will move up and down. These effects reflect the gradual shifting of phase between E₁ and E₂.

Calibration

To apply the technique, we must obviously calibrate the sweep frequency controls of the oscilloscope. Where the fine-frequency control is not marked with a subdivided scale, a dial plate with a hundred divisions may be fixed in place behind it. An audio or other low-frequency oscillator may be used. Connect the oscillator output to the vertical terminals of the oscilloscope and, for each frequency at which calibration is made, adjust the scope controls to obtain a single-cycle display.

During calibration, keep the sync-amplitude control of the scope adjusted to its lowest usable setting. This prevents excessive "pulling" of the sweep frequency and permits the greatest possible accuracy. During actual resonance and LC tests. the sync-amplitude control is set to zero. Despite the fact that the multivibrator of the scope's sweep generator will be free-running with no sync, its stability will be adequate in most cases. Nearly all oscilloscopes today, including some less expensive ones, use some form of voltage regulation, insuring a reasonable amount of frequency stability.

Arbitrary markings rather than actual frequencies should be marked on the scope panel. Actual calibration frequencies should be plotted on graph paper. In this way, a separate curve for each position of the coarse frequency control can be made up, and all curves may be plotted on the same reference sheet. Semi-log graph paper was found to be most practical.

Resonance Testing

To determine the resonant frequency of a parallel circuit, connect it to the oscilloscope as shown in Fig. 2, and adjust sweep frequency to obtain a single-cycle display while maximizing pattern height. Resonant frequency may then be read from the calibration curve.

Conversely, to adjust an LC circuit to a particular frequency, set the scope controls to that frequency and manipulate the value of either L or C to produce the characteristic pattern. The direction in which the parallel combination is off may be determined by comparing the shape of the initial pattern observed with those in Fig. 1.

One practical application of the method has been in testing flyback transformers, by measuring their self-resonant frequency. With the TV receiver de-energized, connect the high end of the flyback transformer to the oscilloscope through the two isolation resistors, as shown, and connect the low end of the transformer to the scope's ground terminal. This self-resonant frequency will vary considerably from one type of set to another, depending on design of the transformer itself and differences in circuit loading. It will help to record the normal frequency for each type of circuit design encountered for later comparison.

In testing the flyback circuit of a suspected receiver, moderate deviation from the normal frequency may be expected due to manufacturing tolerances. However circuit defects, such as open or shorted windings and cracked or loose cores, will result in a marked change in inductance and therefore a large change in resonant frequency. Is it also possible, as in other flyback testing techniques, to unload the transformer gradually by disconnecting associated components one at a time to localize a defect.

Measuring Capacitance

We can determine the value of an inductor or capacitor in a tank circuit if the resonant frequency and the value of the other component in the LC combination are known. Of the two methods available for measuring capacitance, the greater accuracy and simplicity of one of them makes it the strongly preferred technique. In addition to one (or more) inductor chosen as a standard reference, it relies on calibration against several known capacitors. A capacitor decade box or a sequence of other accurate capacitors will serve.

Using the arrangement of Fig. 2, each of the capacitors is connected in turn across the reference inductor. The value of the latter need not be known exactly. With each capacitor, the scope's f_s is adjusted to equal f_r. A sheet of graph paper is then used to record the position of the sweep-frequency controls for each known value of capacitance, and a curve may be plotted from these individual readings. Calibration in terms of sweep frequency is not necessary.

To measure an unknown capacitor, connect it across the reference inductance in the test circuit and adjust the sweep frequency for resonance. The value of C may then be found by direct reference to the calibration curve. Neither the sweep frequency, the exact value of the inductor, nor any other characteristics of the latter need be taken into account once it has been chosen as the standard. Experimentation shows that a choke of about 60 millihenrys can be used to measure capacitance from 100 μμf. to 0.1 μf. High-"Q" inductors are preferred.

The alternative method of measuring C uses the curves already plotted for resonance tests along with the known inductor already noted. In addition, the familiar formulas involving reactance and resonance will have to be used for calculation of values. Even here, the paperwork can be simplified by using a reactance slide rule. One such inexpensive unit is made by Shure Brothers, Inc. Nevertheless, the technique must take into account additional factors that will not be involved in the first method described for measuring capacitance. For example, the reference inductor will have a certain amount of distributed shunt capacitance across its terminals, rendering it self-resonant at some frequency. This capacitance, C_o, is across any external capacitor that may be in parallel with the inductor.

If the inductance is known to start with, C_o may be found by determining the self-resonant frequency and using the formulas or the reactance slide rule. To measure an unknown capacitor, connect it in parallel with the inductor in the test circuit and find f_r. From this frequency and the known value of L, the value of C may be worked out or read on the reactance calculator. From the value thus obtained, C_o should be subtracted. Circuit "Q" also can be a factor if an attempt is made to use an inductor over too wide a range of capacitance values. If circuit "Q" is much less than ten, considerable error can result. For a particular inductor, it is wise to limit the values of C that are used to measure over a range that insures a circuit "Q" of ten or more. The latter factor may also be calculated with the reactance slide rule.

Measuring Inductance

Capacitors of known value will obviously be needed to determine the inductance of unknown coils, and such factors as "Q" and C_o are also important. However a simple method with few pitfalls does exist.

First find the self-resonant frequency, f_o, of the unknown inductor. Next, shunt sufficient known capacitance across this inductor so that f_r for the combination is about one-tenth of f_o. Under these conditions, C_o will be small compared to C, so that the former will not cause significant error. Also, circuit "Q" will generally be above ten. Using f_r and the added shunt capacitance as the known quantities, the inductance can be found using the formula L = 1/4π²f_r²C or from the reac­tance calculator.

Summary

The measurement of low-frequency parallel-resonant circuits and of capacitance, using the methods recommended here based on appropriate calculation curves, are straightforward and reliable. Measurements involving more than one step and the calculator (or formulas) will also be found useful to those who have no other suitable equipment for making such checks.

Accuracies will obviously not approach those obtainable by producing nulls on the bridges in laboratory-quality equipment. However, there is a question as to how much accuracy is actually needed. Most measurements made by the methods described here fell within five per-cent.

A final word of caution: some types of inductors with powdered-iron cores are quite non-linear, inductance varying with applied voltage and frequency. These should be avoided as reference inductors. No simple correction factors will compensate for the errors they introduce. As to capacitors, paper and mica units show relatively small changes in value even at higher frequencies and also have high "Q."