|
April 1969 Electronics World
 Table of Contents
Table of Contents
Wax nostalgic about and learn from the history of early electronics. See articles
from
Electronics World, published May 1959
- December 1971. All copyrights hereby acknowledged.
|
Filters has always been one of
my favorite topics. I gained a real appreciation for and understanding of them when
drudging through the mathematics behind the curves in college courses. BTW, for
anyone out there thinking about taking up engineering as a career; i.e., getting an
engineering degree, it is vitally important that you fully comprehend the concept of
Laplace and Fourier transforms because when you get to the point that you need to
employ them in your primary classes, having to struggle with the basic math while
learning to apply it to circuits, mechanics, etc., will almost surely cause you to
fail. Anyway, this article from a 1969 issue of Electronics World
magazine does a nice job of
introducing the four fundamental filter pass types (not including all-pass) and
discussing the concepts of amplitude and phase relationships. Any filter primer
written today would include the same material, except you probably would not have
ever heard of the image parameter method of filter design, which was the in thing
before desktop computers were available to do the hard work.
The Importance of Filters

The author, Assoc. Professor of Electrical Engineering at Pratt Institute,
received his B.E.E. cum laude from CCNY in 1951 and attended Columbia and Hofstra Universities
(M.A. in Physics, 1958). His areas of interest are solid-state electronics and computer
logic. He is the co-author of "Semiconductor Fundamentals: Devices and Circuits" and
is currently at work on a new book, "Electronic Circuit Analysis" which will be published
very soon.
By A. H. Seidman / Contributing Editor
Once the image-parameter method was the only good approach to filter design. Now it
is modern network synthesis and computers which guarantee better products.
A filter is a frequency-sensitive component which is able to pass, with minimum attenuation,
a select range of frequencies while suppressing the transmission of unwanted frequencies
outside this band. Applications of filters are numerous, covering frequencies from less
than a hertz in seismology to gigahertz in microwave work. Most filters are custom-made
and some five-hundred companies are competing for a market currently estimated to be
$40 million annually and promising to double by 1972.
Because of the widespread use of computers, filter technology in the past few years
has come into its own as a sophisticated specialty. Nearly any filter can be designed
using a computer. Computerized sensitivity studies of such items as component tolerance,
"Q", and environmental factors help in designing a practical filter that is reliable
and meets specifications. Because of the complexity of modern technology, filter requirements
have become more sophisticated than they were a decade ago when the engineer could design
his filter by using suitable tables.
Today, a special brand of expertise is required. There are filter specialists who
design and make filters to satisfy the particular customer requirements. There are filter
houses which can provide any filter design, using lumped, distributed, or other components.
But many others tend to specialize and offer only crystal, ceramic, mechanical, or microwave
filters. In general, except for relatively simple designs, it seldom pays an engineer
to design and build a filter in house. More important is how he selects and specifies
filters. This Special Section outlines these techniques.
What's Available?
If one were able to build the ideal filter, its characteristics would be as shown
in Fig. 1. The passband has unity gain, permitting signals in the range of frequencies
defined by f2-f1 to be transmitted without any
attenuation. In the region outside the passband, referred to as the stopband, 100 percent
suppression of frequencies is obtained. The transition from the pass- to stopband or
vice versa is over zero frequency (instantaneous). And an examination of the phase characteristics
shows that the phase shift changes linearly with frequency in the passband. Actually,
filters do not possess zero attenuation in the passband and suppression in the stopband
is not infinite. Furthermore, the transition between bands is gradual and the phase shift
is nonlinear.

Fig. 1. "Ideal", and unobtainable, filter characteristics. Compare
this graph with those for practical designs, Fig. 2.
The filter designer must approximate ideal filter characteristics as closely as possible
with combinations of passive elements like inductors and capacitors (LC filters); with
resonant transducers (crystal, ceramic, and mechanical filters); combinations of an amplifier
and passive components (active filters); and, at microwave frequencies, distributed,
cavity, and strip-line filters. These subjects are explored in depth in the remaining
articles of this Special Section.
In terms of frequency discrimination properties, there are tour distinct types of
filters: low-pass, high-pass, bandpass, and band-reject types. Typical amplitude and
phase-shift response curves for the filters are given in Fig. 2.
Low-pass filters pass frequencies from zero to a higher or cut-off point. In general,
an RC integrating network is considered a low-pass filter. On the other hand, high-pass
filters attenuate frequencies below a specified cut-off point, passing all other frequencies
beyond this point un-attenuated. Examples of high-pass filters are the simple RC differentiating
network and the waveguide used at microwave frequencies. In both cases, the cut-off frequency
is taken at the -3 dB point.
The bandpass filter passes a group of frequencies between specified lower- and upper-cut-off
frequencies. Typically, bandpass filters are used in the i.f. stages of a receiver. The
band-reject filter can be thought of as an upside-down bandpass filter, rejecting frequencies
between the cut-off points and passing all other frequencies without attenuation.
Filter design is based on mathematics and modern network synthesis. In the past, filter
design was based on the image-parameter method, where a lumped network is described in
terms of a distributed network, like a transmission line. Today, however, the polynomial
method, also called the exact or insertion-loss method. is usually the basis of filter
designs, This method tackles the filter as a lumped-parameter system and deals directly
with the various parameters that characterize the filter. Its drawback is the inordinate
amount of work required to obtain values for the filter elements; this labor means nothing,
however, when calculations are computerized.

Fig. 2(A) - Characteristics of four basic filters using LC elements
- Low-pass

Fig. 2(B) - Characteristics of four basic filters using LC elements
- High-pass

Fig. 2(C) - Characteristics of four basic filters using LC elements
- Band-pass

Fig. 2(D) - Characteristics of four basic filters using LC elements
- Band-reject
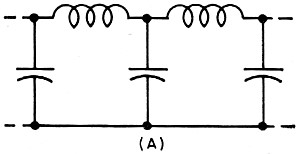
Fig. 3(A) - Butterworth and Chebyshev filters
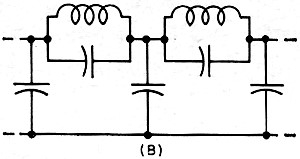
Fig. 3(B) - Elliptic filters.

Fig. 4. Test circuit for measuring insertion loss of filter.
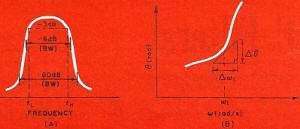
Fig. 5(A) - Defining shape factor and percentage bandwidth. (B) -
Determining the phase slope of the filter. See text.

Fig. 6. Procedures for measuring impedance of a filter.
A number of classic filter designs have evolved, using LC sections. To gain some insight
into what may be expected of filters. three of these structures will be examined briefly:
the Butterworth, Chebyshev, and elliptic filters. Their basic forms, using the low-pass
filter as an example, are shown in Fig. 3.
The Butterworth filter, also referred to as a maximally flat filter, is characterized
by a relatively flat response and no ripple in the passband. The roll-off, that is, the
decrease in gain beyond the cut-off frequency, approximates -18 dB per octave for a section.
In terms of mathematics, the filter is simple to handle, having fair phase and good amplitude
response. Actually, however, its cut-off frequency is poorly defined, making it unsuitable
for applications demanding a uniform transmission of frequencies in the passband and
fast roll-off.
The Chebyshev filter has a sharper cut-off than the Butterworth, but exhibits ripple
in the passband; the ripple is 0.1 to 3 percent, or greater, of maximum signal amplitude.
If one can tolerate greater ripple, a trade-off is possible to obtain sharper cut-off.
The Chebyshev filter provides a relatively constant amplitude in the passband.
Sharper cut-off than that obtainable with either the Butterworth or Chebyshev filters
is realized with the elliptic filter. But, besides having ripple in the passband, the
elliptic filter also exhibits ripple in the stopband, Of the three filters, the elliptic
generally provides the best performance with a minimum number of filter sections. Other
classical LC filters are the Bessel and Gaussian types. Mechanical, crystal, and active
filters can also exhibit characteristics similar to LC filters.
Our discussion of filters has tacitly assumed ideal components - a convenient fiction
that serves to simplify the many calculations in synthesizing filters. To account for
real lossy components, like inductors and capacitors, a technique called predistortion
is used by the experts. Expected changes in filter performance, owing to lossy components,
are included in the evaluations of polynomials used to describe filter operation. When
done on a computer, the task is relatively easy.
Filter Terminology
We have already alluded to some of the terminology, like passband, stopband, and roll-off,
that is peculiar to filters. To specify filters, the engineer must be sure what he is
talking about. In this section we shall consider definitions of terms used to characterize
filters, as used by industry and the military. Wherever appropriate, test circuits employed
in establishing some of the definitions will also be examined.
Insertion loss indicates how effective attenuation of signal frequencies is in either
the passband or stopband of the filter. A test circuit for measuring insertion loss is
shown in Fig. 4. ZS and ZL are the source and load impedances,
respectively; their values must be stated when specifying the insertion loss of a filter.
With the d.p.d.t. switch in position 1, the filter is removed from the circuit. Voltage
(E1) across load ZL, is measured for the frequency or range of frequencies
of interest. When the switch is thrown to position 2, the filter is in the test circuit
and voltage E2 is recorded (for the same range of frequencies used in the previous measurement).
Insertion loss (IL in dB) is defined as: IL = 20 log10 (E1/E2).
Discrimination is a useful criterion for comparing the attenuation in a filter between
a chosen reference frequency, usually the frequency corresponding to maximum output voltage,
and- a second frequency, often in the stopband. The test setup used is the same as that
for measuring insertion loss, with measurements of insertion loss made at the reference
frequency and the second frequency. The algebraic difference, in dB, in the two measurements
yields the discrimination, designated alpha: α = IL (ref freq.) - IL
(second freq.).
The cut-off frequency is the frequency at which the maximum specified insertion loss
occurs in the passband. Typically, it is -3dB, but it can he any selected level.
Because roll-off from the pass- to stopband is gradual, a transition region exists.
This region may be specified as the difference between the cut-off frequency and the
frequency corresponding to the minimum value of insertion loss in the stopband.
Two terms used to characterize bandpass filters are shape factor and percent bandwidth
. A typical amplitude response curve for a bandpass filter is shown in Fig, 5A. Shape
factor is defined as the ratio of bandwidths between two specified values of insertion
loss in the passband. Often the -6 dB and -60 dB points are selected; assuming this to
be the case, the shape factor is Shape factor = BW (-60 dB) /BW (-6 dB).
Percent bandwidth is defined as: EQUATION HERE, where fH and
fL. are the upper and lower -3 dB frequency points, respectively.
Ripple in the passband or stopband can be cited either in dB or percent.
Except for the ideal filter, the phase-shift response of filters is nonlinear. A useful
measure of the nonlinearity is the phase slope obtained by drawing a line tangent to
the phase-shift curve at the frequency in question (see Fig. 5B). A triangle is drawn
and the phase slope, in seconds is defined as: Phase slope = Δθ / Δω
.
Group delay is the delay of frequencies transmitted through the passband. If the delay
is flat, all frequencies are delayed by the same amount. Group delay is equal to the
phase slope at a stated frequency.
The transient response of a filter is its response to a step function. In practice,
the step is approximated by a low-frequency square wave. The output response of the filter
will appear as a damped sinusoid having a maximum overshoot and ringing. Where the transient
performance of filters is important to the application, a figure of permissible overshoot
and ringing should be specified.
Out-put and input impedance of a filter at various frequencies may be determined with
the test setup of Fig. 6. Source ES is a variable frequency source; the filter
is terminated in a specified impedance. By definition, the magnitude of the input (or
output) impedance is the magnitude of the impressed voltage |EI| across the
filter, divided by the magnitude of the input current. Because current meters tend to
be inaccurate at higher frequencies, the input current is determined by measuring the
voltage magnitude |ER|, using an off-ground or battery-operated meter, across
resistance R. The input (or output) impedance, Z, is: Z = |EI / ER
| (R).
At the outset the engineer should have a good idea of what the filter he needs is
expected to do. He should know, for example, what the filter characteristics should look
like, temperature range of operation, and the impedance terminations the filter will
see when installed in the circuit. To assist the engineer, some companies provide nomograms,
charts, or graphs to enable him to specify a filter. Sales and applications engineers
are also available to help the engineer arrive at a realistic filter specification. What
must never be done is to over-specify; over-specification results in higher costs and
bulkier filters.
Filters come in many forms other than LC (or RC) structures. As described in the following
articles, filters using mechanical transducers, like ceramic and crystal, offer interesting
design opportunities; at low frequencies. the active filter can be a possible choice.
The engineer should investigate all possibilities before making his final selection.
What are some things the filter designer must know to ensure that you, the engineer,
will get the most filter for your dollar? He must know the magnitude of signals to be
applied to the filter and their waveshape. If high-amplitude signals are present, power
levels may become a significant consideration which could lead to larger, heavier, and
costlier units. For this reason, filters should be used in low-level stages.
If the waveshape is appreciably nonsinusoidal, the transient response becomes important;
this requires the specification of values of permissible overshoot and ringing. If the
filter is going to see d.c. levels in addition to the signal, this must also be stated
in the filter specification.
All filters exhibit a nonlinear phase shift and a varying phase slope. In applications
like data transmission systems, where a constant phase slope over some specific operating
region is required to ensure flat group delay, this condition must be specified. A constant
phase slope requirement will raise filter costs; therefore it should be specified only
if absolutely essential.
As previously stated, early filter designs used the image-parameter method, where
equal source and load impedances are considered essential for optimum filter performance.
But today, thanks to the computer, the polynomial method is generally used to synthesize
filters. With this technique, the actual source and load impedances the filter sees when
placed in the circuit are the significant parameters. If parallel operation is necessary,
as in some telemetry applications, this should be made known to the designer so he can
consider the stop-band impedance characteristics of the filters as well as minimize interactions
between the parallel combination.
The maximum ripple that can be tolerated in the pass- or stopband should be specified.
Achieving low ripple often entails more filter sections and high-"Q" components, resulting
in greater filter costs. For these reasons, an engineer should never over-specify but
determine realistically how much ripple he can "live with."
A realistic appraisal of environmental conditions under which the filter will operate
is a worthwhile undertaking. A wider temperature range than needed could mean that highly
"stable components would be required, again resulting in higher filter costs. In addition,
excessive shock and vibration requirements increase costs and lead to bulkier filter
designs.
A number of companies offer brochures relating to filter operation and design. A sampling
of some that may be of interest to the reader are: "Wave Filters: Their Design and Specifications"
by ADC Products Inc., Minneapolis, Minn. Burr-Brown. of Tucson, Arizona has a well-written
booklet, covering active filters, entitled "Handbook of Operational Amplifier Active
RC Networks." Crystal filters are treated in "Recent Developments in Crystal Filters"
issued by Damon Engineering Inc., Needham Heights, Mass. For military applications, MIL-F-18327C
(May, 1966 is a general specification for filters.
|



















