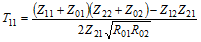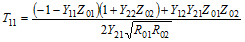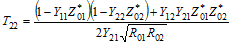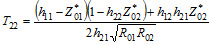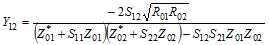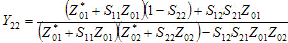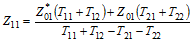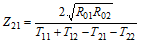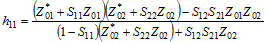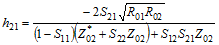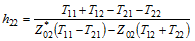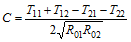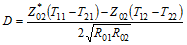Conversion formulas between various forms of 2-port network electrical parameters
is difficult to find (at least when I first posted these way back in
2001), so once I finally located the paper that included them1, I felt it was my duty to publish it for public
access. The paper is available on the IEEE website by subscribers only. None that
I found also include the correction paper2
published a year later that addresses some of the technicalities of the S- and T-parameter
translations when complex impedance reference planes are used. In order to avoid
those sticky issues, I have reproduced only the sets of translations that are unaffected.
Many thanks to Mr. Frickey for his unique work.
The 2-port network shown to the above is representative of what is implied in
the application of these equations. Basic relationships of voltage and current are
given in the table to the right. Many other sources exist on the particulars of
2-port network analysis, so it will not be covered here.
All of the parameter equations make use of complex values for all numbers of
impedance and the resulting matrix parameters, i.e., Z = R ± jX.
If you do not already know, here is the meaning of each type of parameter matrix:
S (scattering), Y (admittance), Z (impedance), h (hybrid), ABCD (chain), and T (chain
scattering or chain transfer).
These are all I have, so please do not write to ask if I have others.
1. IEEE Transactions on Microwave Theory and Techniques. Vol. 42, No
2. February 1994. Conversions Between S, Z, Y, h, ABCD, and T Parameters which are
Valid for Complex Source and Load Impedances. By Dean A. Frickey, Member, IEEE
2. IEEE Transactions on Microwave Theory and Techniques. Vol 43, No
4. April 1995. A correction was printed by Roger B. Marks and Dylan F. Williams.
3. I1 formula corrected to use V2 rather than
V1. Thanks to Christoph T. for noticing.
4. Here is Andy H.'s message:
In regards to the page dealing with two port conversions: https://www.rfcafe.com/references/electrical/s-h-y-z.htm.
Frickey's original work is indeed correct. I put the equations into Sympy and solved
them symbolically to show they match as given below. I also implemented them in
Python to numerically show they are correct. Finally, I implemented Louis J.'s version
and those only work for real-valued impedances. This is apparent as no components
of Z01 or Z02 are ever conjugated in his expressions.
import sympy as sp
t11, t12, t21, t22 = sp.symbols('t11, t12, t21, t22') h11, h12, h21, h22 = sp.symbols('h11,
h12, h21, h22') z01, z02, z01c, z02c, R = sp.symbols('z01, z02, z01c, z02c, R')
eq1 = sp.Eq(( (-h11-z01) * (1+h22*z02) + h12*h21*z02 ) / (2*h21*R), t11) eq2
= sp.Eq(( (h11+z01) * (1-h22*z02c) + h12*h21*z02c ) / (2*h21*R), t12) eq3 = sp.Eq((
(z01c-h11) * (1+h22*z02) + h12*h21*z02 ) / (2*h21*R), t21) eq4 = sp.Eq(( (h11-z01c)
* (1-h22*z02c) + h12*h21*z02c ) / (2*h21*R), t22)
ans = sp.solve((eq1, eq2, eq3, eq4), (h11, h12, h21, h22))
print(ans)
[((t11*z01c*z02c - t12*z01c*z02 + t21*z01*z02c - t22*z01*z02) / (t11*z02c - t12*z02
- t21*z02c + t22*z02),
2*R*(t11*t22 - t12*t21) / (t11*z02c - t12*z02 - t21*z02c + t22*z02),
-(z01 + z01c)*(z02 + z02c) / (2*R*(t11*z02c - t12*z02 - t21*z02c + t22*z02)),
(t11 + t12 - t21 - t22) / (t11*z02c - t12*z02 - t21*z02c + t22*z02))]
----- Comparison with Complex Impedances ----- import numpy as np
def t_to_h_frickey(t, z0):
z0c = np.matrix.conj(z0)
h = np.zeros([2,2], dtype=complex)
denominator = z0c[1] * (t[0,0] - t[1,0]) - z0[1] * (t[0,1] - t[1,1])
h[0,0] = z0c[1]*(t[0,0] * z0c[0] + t[1,0] * z0[0]) - z0[1] * (t[0,1] * z0c[0]
+ t[1,1] * z0[0]) h[0,1] = 2 * np.sqrt(z0[0].real * z0[1].real) * (t[0,0] * t[1,1]
- t[0,1] * t[1,0]) h[1,0] = -2 * np.sqrt(z0[0].real * z0[1].real) h[1,1] = t[0,0]
+ t[0,1] - t[1,0] - t[1,1]
return h / denominator
def t_to_h_louis(t, z0):
z0c = np.matrix.conj(z0)
h = np.zeros([2,2], dtype=complex)
denominator = t[1,1] + t[0,0] - t[0,1] - t[1,0]
h[0,0] = z0[0] * (-t[1,1] + t[1,0] + t[0,0] - t[0,1]) h[0,1] = 2 * (t[0,0] *
t[1,1] - t[0,1] * t[1,0]) * np.sqrt(z0[0].real * z0[1].real) / z0[1] h[1,0] = -2
* z0[0] / np.sqrt(z0[0].real * z0[1].real) h[1,1] = (-t[1,1] + t[0,1] + t[0,0] -
t[1,0]) / z0[1]
return h / denominator
def h_to_t(h, z0):
z0c = np.matrix.conj(z0)
t = np.zeros([2,2], dtype=complex)
denominator = 2 * h[1,0] * np.sqrt(z0[0].real * z0[1].real)
t[0,0] = (-h[0,0] - z0[0]) * (1 + h[1,1] * z0[1]) + h[0,1] * h[1,0] * z0[1] t[0,1]
= (h[0,0] + z0[0]) * (1 - h[1,1] * z0c[1]) + h[0,1] * h[1,0] * z0c[1] t[1,0] = (z0c[0]
- h[0,0]) * (1 + h[1,1] * z0[1]) + h[0,1] * h[1,0] * z0[1] t[1,1] = (h[0,0] - z0c[0])
* (1 - h[1,1] * z0c[1]) + h[0,1] * h[1,0] * z0c[1]
return t / denominator
t11 = 1 + 1j * 2 t12 = 5 - 1j * 8 t21 = -4 + 1j * 3 t22 = 2 + 1j * 1
t = np.array([[t11, t12], [t21, t22]])
# T <--> H z1, z2 = 50 + 10j, 50 - 10j
h = t_to_h_frickey(t, np.array([z1, z2])) print('Frickey:') print(f'Conversion
from T to H \n{h}') print(f'Conversion from H to T \n{h_to_t(h, np.array([z1, z2]))}')
h = t_to_h_louis(t, np.array([z1, z2])) print('Louis:') print(f'Conversion from
T to H \n{h}') print(f'Conversion from H to T \n{h_to_t(h, np.array([z1, z2]))}')
Frickey: Conversion from T to H [[ 3.90532544e+01+5.62721893e+01j -7.75147929e+00-2.39644970e+00j]
[-7.39644970e-02+1.77514793e-01j -1.18343195e-02-2.15976331e-02j]]
Conversion from H to T [[ 1.+2.j 5.-8.j] [-4.+3.j 2.+1.j]]
Louis: Conversion from T to H [[ 4.05882353e+01+8.76470588e+01j -9.43438914e+00-3.41628959e+00j]
[-1.05882353e-01+2.23529412e-01j -1.33484163e-02-2.73755656e-02j]]
Conversion from H to T [[ 1. +2.j 5.92307692-661538462j] [-3.61538462+3.92307692j
2.84615385+1.07692308j]]
----- Comparison with Real-Valued Impedances -----
t11 = 1 + 1j * 2 t12 = 5 - 1j * 8 t21 = -4 + 1j * 3 t22 = 2 + 1j * 1
t = np.array([[t11, t12], [t21, t22]])
# T <--> H z1, z2 = 50 + 0j, 50 - 0j
h = t_to_h_frickey(t, np.array([z1, z2])) print('Frickey:') print(f'Conversion
from T to H \n{h}') print(f'Conversion from H to T \n{h_to_t(h, np.array([z1, z2]))}')
h = t_to_h_louis(t, np.array([z1, z2])) print('Louis:') print(f'Conversion from
T to H \n{h}') print(f'Conversion from H to T \n{h_to_t(h, np.array([z1, z2]))}')
Frickey: Conversion from T to H [[ 5.58823529e+01+7.64705882e+01j -1.01176471e+01-1.52941176e+00j]
[-5.88235294e-02+2.35294118e-01j -1.88235294e-02-2.47058824e-02j]] Conversion from
H to T [[ 1.+2.j 5.-8.j] [-4.+3.j 2.+1.j]]
Louis: Conversion from T to H [[ 5.58823529e+01+7.64705882e+01j -1.01176471e+01-1.52941176e+00j]
[-5.88235294e-02+2.35294118e-01j -1.88235294e-02-2.47058824e-02j]] Conversion from
H to T [[ 1.+2.j 5.-8.j] [-4.+3.j 2.+1.j]]
Then:
I went down a rabbit hole and programmed (in Python) all of the conversions in
the paper, and made test cases that I put in a separate Python file. The test cases
use measured data from an Analog Devices HMC455LP3 high output IP3 GaAs InGaP heterojunction
bipolar transistor. I have attached both files and I will default to you as to whether
or not to post the contents.
# IEEE TRANSACTIONS ON MICROWAVE THEORY AND TECHNIQUES. VOL 42, NO 2. FEBRUARY
1994
# Conversions Between S, Z, Y, h, ABCD, and T Parameters which are Valid
for Complex Source and Load Impedances
# Dean A. Frickey, Member, EEE
# Tables I and II
import numpy as np
from two_port_conversions import
*
""" Testing """
# Analog Devices - HMC455LP3 - S parameters
# High
output IP3 GaAs InGaP Heterojunction Bipolar Transistor
# MHz S (Magntidue
and Angle (deg))
# 1487.273 0.409 160.117 4.367 163.864 0.063 115.967 0.254 -132.654
s11 = 0.409 * np.exp(1j * np.radians(160.117))
s12 = 4.367 * np.exp(1j *
np.radians(163.864))
s21 = 0.063 * np.exp(1j * np.radians(115.967))
s22 =
0.254 * np.exp(1j * np.radians(-132.654))
s_orig = np.array([[s11, s12],
[s21, s22]])
# Data specified at 50 Ohms (adding small complex component
to test conversions)
z1, z2 = 50 + 0.01j, 50 - 0.02j
z0 = np.array([z1, z2])
""" Conversions """
print(f'Original S: \n{s_orig}\n')
# S -->
Z --> T --> Z --> S
z = s_to_z(s_orig, z0)
t = z_to_t(z, z0)
z
= t_to_z(t, z0)
s = z_to_s(z, z0)
print(f'Test (S --> Z --> T -->
Z --> S): \n{s}\n')
# S --> Y --> T --> Y --> S
y = s_to_y(s_orig,
z0)
t = y_to_t(y, z0)
y = t_to_y(t, z0)
s = y_to_s(y, z0)
print(f'Test
(S --> Y --> T --> Y --> S): \n{s}\n')
# S --> H --> T
--> H --> S
h = s_to_h(s_orig, z0)
t = h_to_t(h, z0)
h = t_to_h(t,
z0)
s = h_to_s(h, z0)
print(f'Test (S --> H --> T --> H --> S):
\n{s}\n')
# S --> ABCD --> T --> ABCD --> S
abcd = s_to_abcd(s_orig,
z0)
t = abcd_to_t(abcd, z0)
abcd = t_to_abcd(t, z0)
s = abcd_to_s(abcd,
z0)
print(f'Test (S --> ABCD --> T --> ABCD --> S): \n{s}\n')
# IEEE TRANSACTIONS ON MICROWAVE THEORY AND TECHNIQUES. VOL 42, NO 2. FEBRUARY
1994
# Conversions Between S, Z, Y, h, ABCD, and T Parameters which are Valid
for Complex Source and Load Impedances
# Dean A. Frickey, Member, EEE
# Tables I and II
import numpy as np
def s_to_z(s, z0):
""" Scattering
(S) to Impedance (Z)
:param s: The scattering matrix.
:param z0: The port
impedances (Ohms).
:return: The impedance matrix.
"""
# Calculate the conjugate
of the port impedances
z0c = np.matrix.conj(z0)
# Initialize the output
array
z = np.zeros([2,2], dtype=complex)
# Calculate the denominator
denominator = (1 - s[0,0]) * (1 - s[1,1]) - s[0,1] * s[1,0]
# Calculate the
numerators
z[0,0] = (z0c[0] + s[0,0] * z0[0]) * (1 - s[1,1]) + s[0,1] * s[1,0]
* z0[0]
z[0,1] = 2 * s[0,1] * np.sqrt(z0[0].real * z0[1].real)
z[1,0] = 2
* s[1,0] * np.sqrt(z0[0].real * z0[1].real)
z[1,1] = (1 - s[0,0]) * (z0c[1] +
s[1,1] * z0[1]) + s[0,1] * s[1,0] * z0[1]
# Return the conversion
return
z / denominator
def z_to_s(z, z0):
""" Impedance (Z) to Scattering
(S)
:param z: The impedance matrix.
:param z0: The port impedances (Ohms).
:return: The scattering matrix.
"""
# Calculate the conjugate of the port
impedances
z0c = np.matrix.conj(z0)
# Initialize the output array
s
= np.zeros([2,2], dtype=complex)
# Calculate the denominator
denominator
= (z[0,0] + z0[0]) * (z[1,1] + z0[1]) - z[0,1] * z[1,0]
# Calculate the numerators
s[0,0] = (z[0,0] - z0c[0]) * (z[1,1] + z0[1]) - z[0,1] * z[1,0]
s[0,1] = 2 *
z[0,1] * np.sqrt(z0[0].real * z0[1].real)
s[1,0] = 2 * z[1,0] * np.sqrt(z0[0].real
* z0[1].real)
s[1,1] = (z[0,0] + z0[0]) * (z[1,1] - z0c[1]) - z[0,1] * z[1,0]
# Return the conversion
return s / denominator
def s_to_y(s, z0):
""" Scattering (S) to Admittance (Y)
:param s: The scattering matrix.
:param z0: The port impedances (Ohms).
:return: The admittance matrix.
"""
# Calculate the conjugate of the port impedances
z0c = np.matrix.conj(z0)
# Initialize the output array
y = np.zeros([2,2], dtype=complex)
#
Calculate the denominator
denominator = (z0c[0] + s[0,0] * z0[0]) * (z0c[1] +
s[1,1] * z0[1]) - s[0,1] * s[1,0] * z0[0] * z0[1]
# Calculate the numerators
y[0,0] = (1 - s[0,0]) * (z0c[1] + s[1,1] * z0[1]) + s[0,1] * s[1,0] * z0[1]
y[0,1]
= -2 * s[0,1] * np.sqrt(z0[0].real * z0[1].real)
y[1,0] = -2 * s[1,0] * np.sqrt(z0[0].real
* z0[1].real)
y[1,1] = (z0c[0] + s[0,0] * z0[0]) * (1 - s[1,1]) + s[0,1] * s[1,0]
* z0[0]
# Return the conversion
return y / denominator
def
y_to_s(y, z0):
""" Admittance (Y) to Scattering (S)
:param y: The admittance
matrix.
:param z0: The port impedances (Ohms).
:return: The scattering matrix.
"""
# Calculate the conjugate of the port impedances
z0c = np.matrix.conj(z0)
# Initialize the output array
s = np.zeros([2,2], dtype=complex)
#
Calculate the denominator
denominator = (1 + y[0,0] * z0[0]) * (1 + y[1,1] *
z0[1]) - y[0,1] * y[1,0] * z0[0] * z0[1]
# Calculate the numerators
s[0,0]
= (1 - y[0,0] * z0c[0]) * (1 + y[1,1] * z0[1]) + y[0,1] * y[1,0] * z0c[0] * z0[1]
s[0,1] = -2 * y[0,1] * np.sqrt(z0[0].real * z0[1].real)
s[1,0] = -2 * y[1,0]
* np.sqrt(z0[0].real * z0[1].real)
s[1,1] = (1 + y[0,0] * z0[0]) * (1 - y[1,1]
* z0c[1]) + y[0,1] * y[1,0] * z0[0] * z0c[1]
# Return the conversion
return
s / denominator
def s_to_h(s, z0):
""" Scattering (S) to Hybrid (H)
:param s: The scattering matrix.
:param z0: The port impedances (Ohms).
:return: The hybrid matrix.
"""
# Calculate the conjugate of the port impedances
z0c = np.matrix.conj(z0)
# Initialize the output array
h = np.zeros([2,2],
dtype=complex)
# Calculate the denominator
denominator = (1 - s[0,0])
* (z0c[1] + s[1,1] * z0[1]) + s[0,1] * s[1,0] * z0[1]
# Calculate the numerators
h[0,0] = (z0c[0] + s[0,0] * z0[0]) * (z0c[1] + s[1,1] * z0[1]) - s[0,1] * s[1,0]
* z0[0] * z0[1]
h[0,1] = 2 * s[0,1] * np.sqrt(z0[0].real * z0[1].real)
h[1,0]
= -2 * s[1,0] * np.sqrt(z0[0].real * z0[1].real)
h[1,1] = (1 - s[0,0]) * (1 -
s[1,1]) - s[0,1] * s[1,0]
# Return the conversion
return h / denominator
def h_to_s(h, z0):
""" Hybrid (H) to Scattering (S)
:param h:
The hybrid matrix.
:param z0: The port impedances (Ohms).
:return: The scattering
matrix.
"""
# Calculate the conjugate of the port impedances
z0c = np.matrix.conj(z0)
# Initialize the output array
s = np.zeros([2,2], dtype=complex)
#
Calculate the denominator
denominator = (z0[0] + h[0,0]) * (1 + h[1,1] * z0[1])
- h[0,1] * h[1,0] * z0[1]
# Calculate the numerators
s[0,0] = (h[0,0]
- z0c[0]) * (1 + h[1,1] * z0[1]) - h[0,1] * h[1,0] * z0[1]
s[0,1] = 2 * h[0,1]
* np.sqrt(z0[0].real * z0[1].real)
s[1,0] = -2 * h[1,0] * np.sqrt(z0[0].real
* z0[1].real)
s[1,1] = (z0[0] + h[0,0]) * (1 - h[1,1] * z0c[1]) + h[0,1] * h[1,0]
* z0c[1]
# Return the conversion
return s / denominator
def
s_to_abcd(s, z0):
""" Scattering to Chain (ABCD)
:param s: The scattering
matrix.
:param z0: The port impedances (Ohms).
:return: The chain matrix.
"""
# Calculate the conjugate of the port impedances
z0c = np.matrix.conj(z0)
# Initialize the output array
ans = np.zeros([2,2], dtype=complex)
# Calculate the denominator
denominator = 2 * s[1,0] * np.sqrt(z0[0].real
* z0[1].real)
# Calculate the numerators
ans[0,0] = (z0c[0] + s[0,0] *
z0[0]) * (1 - s[1,1]) + s[0,1] * s[1,0] * z0[0]
ans[0,1] = (z0c[0] + s[0,0] *
z0[0]) * (z0c[1] + s[1,1] * z0[1]) - s[0,1] * s[1,0] * z0[0] * z0[1]
ans[1,0]
= (1 - s[0,0]) * (1 - s[1,1]) - s[0,1] * s[1,0]
ans[1,1] = (1 - s[0,0]) * (z0c[1]
+ s[1,1] * z0[1]) + s[0,1] * s[1,0] * z0[1]
# Return the conversion
return
ans / denominator
def abcd_to_s(abcd, z0):
""" Chain (ABCD) to Scattering
(S)
:param abcd: The chain matrix.
:param z0: The port impedances (Ohms).
:return: The scattering matrix.
"""
# Break out the components
A = abcd[0,0]
B = abcd[0,1]
C = abcd[1,0]
D = abcd[1,1]
# Calculate the conjugate
of the port impedances
z0c = np.matrix.conj(z0)
# Initialize the output
array
s = np.zeros([2,2], dtype=complex)
# Calculate the denominator
denominator = A * z0[1] + B + C * z0[0] * z0[1] + D * z0[0]
# Calculate the
numerators
s[0,0] = A * z0[1] + B - C * z0c[0] * z0[1] - D * z0c[0]
s[0,1]
= 2 * (A * D - B * C) * np.sqrt(z0[0].real * z0[1].real)
s[1,0] = 2 * np.sqrt(z0[0].real
* z0[1].real)
s[1,1] = -A * z0c[1] + B - C * z0[0] * z0c[1] + D * z0[0]
# Return the conversion
return s / denominator
def t_to_z(t, z0):
""" Chain Transfer (T) to Impedance (Z)
:param t: The chain transfer matrix.
:param z0: The port impedances (Ohms).
:return: The impedance matrix.
"""
# Calculate the conjugate of the port impedances
z0c = np.matrix.conj(z0)
# Initialize the output array
z = np.zeros([2,2], dtype=complex)
#
Calculate the denominator
denominator = t[0,0] + t[0,1] - t[1,0] - t[1,1]
# Calculate the numerators
z[0,0] = z0c[0] * (t[0,0] + t[0,1]) + z0[0] *
(t[1,0] + t[1,1])
z[0,1] = 2 * np.sqrt(z0[0].real * z0[1].real) * (t[0,0] * t[1,1]
- t[0,1] * t[1,0])
z[1,0] = 2 * np.sqrt(z0[0].real * z0[1].real)
z[1,1] =
z0c[1] * (t[0,0] - t[1,0]) - z0[1] * (t[0,1] - t[1,1])
# Return the conversion
return z / denominator
def z_to_t(z, z0):
""" Impedance (Z) to Chain
Transfer (T)
:param z: The impedance matrix.
:param z0: The port impedances
(Ohms).
:return: The chain transfer matrix.
"""
# Calculate the conjugate
of the port impedances
z0c = np.matrix.conj(z0)
# Initialize the output
array
t = np.zeros([2,2], dtype=complex)
# Calculate the denominator
denominator = 2 * z[1,0] * np.sqrt(z0[0].real * z0[1].real)
# Calculate the
numerators
t[0,0] = (z[0,0] + z0[0]) * (z[1,1] + z0[1]) - z[0,1] * z[1,0]
t[0,1] = (z[0,0] + z0[0]) * (z0c[1] - z[1,1]) + z[0,1] * z[1,0]
t[1,0] = (z[0,0]
- z0c[0]) * (z[1,1] + z0[1]) - z[0,1] * z[1,0]
t[1,1] = (z0c[0] - z[0,0]) * (z[1,1]
- z0c[1]) + z[0,1] * z[1,0]
# Return the conversion
return t / denominator
def t_to_y(t, z0):
""" Chain Transfer (T) to Admittance (Y)
:param
t: The chain transfer matrix.
:param z0: The port impedances (Ohms).
:return:
The admittance matrix.
"""
# Calculate the conjugate of the port impedances
z0c = np.matrix.conj(z0)
# Initialize the output array
y = np.zeros([2,2],
dtype=complex)
# Calculate the denominator
denominator = t[0,0] * z0c[0]
* z0c[1] - t[0,1] * z0c[0] * z0[1] + t[1,0] * z0[0] * z0c[1] - t[1,1] * z0[0] *
z0[1]
# Calculate the numerators
y[0,0] = z0c[1] * (t[0,0] - t[1,0]) -
z0[1] * (t[0,1] - t[1,1])
y[0,1] = -2 * np.sqrt(z0[0].real * z0[1].real) * (t[0,0]
* t[1,1] - t[0,1] * t[1,0])
y[1,0] = -2 * np.sqrt(z0[0].real * z0[1].real)
y[1,1] = z0c[0] * (t[0,0] + t[0,1]) + z0[0] * (t[1,0] + t[1,1])
# Return
the conversion
return y / denominator
def y_to_t(y, z0):
""" Admittance
(Y) to Chain Transfer (T)
:param y: The admittance matrix.
:param z0:
The port impedances (Ohms).
:return: The chain transfer matrix.
"""
# Calculate
the conjugate of the port impedances
z0c = np.matrix.conj(z0)
# Initialize
the output array
t = np.zeros([2,2], dtype=complex)
# Calculate the denominator
denominator = 2 * y[1,0] * np.sqrt(z0[0].real * z0[1].real)
# Calculate the
numerators
t[0,0] = (-1 - y[0,0] * z0[0]) * (1 + y[1,1] * z0[1]) + y[0,1] * y[1,0]
* z0[0] * z0[1]
t[0,1] = (1 + y[0,0] * z0[0]) * (1 - y[1,1] * z0c[1]) + y[0,1]
* y[1,0] * z0[0] * z0c[1]
t[1,0] = (y[0,0] * z0c[0] - 1) * (1 + y[1,1] * z0[1])
- y[0,1] * y[1,0] * z0c[0] * z0[1]
t[1,1] = (1 - y[0,0] * z0c[0]) * (1 - y[1,1]
* z0c[1]) - y[0,1] * y[1,0] * z0c[0] * z0c[1]
# Return the conversion
return t / denominator
def t_to_h(t, z0):
""" Chain Transfer (T) to
Hybrid (H)
:param t: The chain transfer matrix.
:param z0: The port impedances
(Ohms).
:return: The hybrid matrix.
"""
# Calculate the conjugate of the
port impedances
z0c = np.matrix.conj(z0)
# Initialize the output array
h = np.zeros([2,2], dtype=complex)
# Calculate the denominator
denominator
= z0c[1] * (t[0,0] - t[1,0]) - z0[1] * (t[0,1] - t[1,1])
# Calculate the
numerators
h[0,0] = z0c[1]*(t[0,0] * z0c[0] + t[1,0] * z0[0]) - z0[1] * (t[0,1]
* z0c[0] + t[1,1] * z0[0])
h[0,1] = 2 * np.sqrt(z0[0].real * z0[1].real) * (t[0,0]
* t[1,1] - t[0,1] * t[1,0])
h[1,0] = -2 * np.sqrt(z0[0].real * z0[1].real)
h[1,1] = t[0,0] + t[0,1] - t[1,0] - t[1,1]
# Return the conversion
return
h / denominator
def h_to_t(h, z0):
""" Hybrid (H) to Chain Transfer
(T)
:param t: The hybrid matrix.
:param z0: The port impedances (Ohms).
:return: The chain transfer matrix.
"""
# Calculate the conjugate of the port
impedances
z0c = np.matrix.conj(z0)
# Initialize the output array
t
= np.zeros([2,2], dtype=complex)
# Calculate the denominator
denominator
= 2 * h[1,0] * np.sqrt(z0[0].real * z0[1].real)
# Calculate the numerators
t[0,0] = (-h[0,0] - z0[0]) * (1 + h[1,1] * z0[1]) + h[0,1] * h[1,0] * z0[1]
t[0,1]
= (h[0,0] + z0[0]) * (1 - h[1,1] * z0c[1]) + h[0,1] * h[1,0] * z0c[1]
t[1,0]
= (z0c[0] - h[0,0]) * (1 + h[1,1] * z0[1]) + h[0,1] * h[1,0] * z0[1]
t[1,1] =
(h[0,0] - z0c[0]) * (1 - h[1,1] * z0c[1]) + h[0,1] * h[1,0] * z0c[1]
# Return
the conversion
return t / denominator
def t_to_abcd(t, z0):
"""
Chain Transfer (T) to Chain (ABCD)
:param t: The chain transfer matrix.
:param z0: The port impedances (Ohms).
:return: The chain matrix.
"""
#
Calculate the conjugate of the port impedances
z0c = np.matrix.conj(z0)
# Initialize the output array
ans = np.zeros([2,2], dtype=complex)
# Calculate the denominator
denominator = 2 * np.sqrt(z0[0].real * z0[1].real)
# Calculate the numerators
ans[0,0] = z0c[0] * (t[0,0] + t[0,1]) + z0[0]
* (t[1,0] + t[1,1])
ans[0,1] = z0c[1] * (t[0,0] * z0c[0] + t[1,0] * z0[0]) -
z0[1] * (t[0,1] * z0c[0] + t[1,1] * z0[0])
ans[1,0] = t[0,0] + t[0,1] - t[1,0]
- t[1,1]
ans[1,1] = z0c[1] * (t[0,0] - t[1,0]) - z0[1] * (t[0,1] - t[1,1])
# Return the conversion
return ans / denominator
def abcd_to_t(abcd,
z0):
""" Chain (ABCD) to Chain Transfer (T)
:param abcd: The chain matrix.
:param z0: The port impedances (Ohms).
:return: The chain transfer matrix.
"""
# Break out the components
A = abcd[0,0]
B = abcd[0,1]
C = abcd[1,0]
D = abcd[1,1]
# Calculate the conjugate of the port impedances
z0c = np.matrix.conj(z0)
# Initialize the output array
t = np.zeros([2,2], dtype=complex)
#
Calculate the denominator
denominator = 2 * np.sqrt(z0[0].real * z0[1].real)
# Calculate the numerators
t[0,0] = A * z0[1] + B + C * z0[0] * z0[1] + D
* z0[0]
t[0,1] = A * z0c[1] - B + C * z0[0] * z0c[1] - D * z0[0]
t[1,0] =
A * z0[1] + B - C * z0c[0] * z0[1] - D * z0c[0]
t[1,1] = A * z0c[1] - B - C *
z0c[0] * z0c[1] + D * z0c[0]
# Return the conversion
return t / denominator
5. Here is Louis J.'s message:







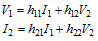

 One of the most
sought-after sets of conversion is from s-parameters to T-parameters, and then back
to s-parameters. This is because matrix multiplications can be performed directly
on T-parameters in order to calculate cascaded component responses. That is, s-parameters
matrices cannot be multiplied in series to obtain cascaded s-parameters, but T-parameters
can be. So, convert your component s-parameters to T-parameters, multiply matrices,
then convert the result back to s-parameters.
One of the most
sought-after sets of conversion is from s-parameters to T-parameters, and then back
to s-parameters. This is because matrix multiplications can be performed directly
on T-parameters in order to calculate cascaded component responses. That is, s-parameters
matrices cannot be multiplied in series to obtain cascaded s-parameters, but T-parameters
can be. So, convert your component s-parameters to T-parameters, multiply matrices,
then convert the result back to s-parameters.