Rationalizing Pi
(i.e., can exactly one full rotation equal an inexact number?)
Kirt's Cogitations™ #262

<Previous                     Next>

Rationalizing Pi

While torturing myself on the elliptical exercise machine in my basement, I often do mental exercises to help pass time during the utterly boring, albeit beneficial, endeavor. Often the routine is no more complicated than dividing elapsed calories shown on the counter display by elapsed time to get a burn rate, then figuring how much longer it will take until my goal is reached (usually between 1,200 and 1,800 calories), all without the benefit of paper, pencil, or calculator. Of course by the time I finally come up with a number, I'm way past the point where the calculations began, so I start over. That reminds me of the old episode of Beverly Hillbillies where Jethro is showing off his new watch to Uncle Jed. Jed asks what time it is, and Jethro says, "Well, the big hand is on the 2 and little hand is on the 12 and the second hand is on the 10, so that makes it uh...., shucks, its not that time anymore." He went through the routine three or four times with no indication that he would ever stop. Finally, Jed asks him, "What's the pert-near time?," to which Jethro responds, "It's pert-near 2:13." ... but I digress.

During my last session on the cursed machine, for some reason I was contemplating pi (π - not yet cancelled by WHO). Pi has been an enigma in the realm of mathematics and physics since it was first recognized as being irrational. The fact that the ratio of a circle's circumference to its diameter is an inexact number has caused enormous amounts of consternation for dogged investigators of the aforementioned phenomenon. Pythagoras is believed to have first noticed the irrationality of certain numerical ratios when even something as basic as the corner-to-corner diagonal of a unit square could not be calculated to a finite precision. In some religious circles (see what I did there?) even contemplating such thoughts caused souls to be burned at the stake for daring to assert that such an imperfection could exist in a perfectly created world. Recall that Galileo was excommunicated for asserting that the earth was not the center of the universe. I kid you not.

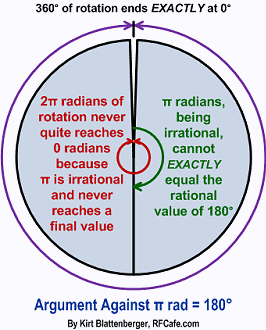
For anyone not familiar with irrational numbers, they are numbers with non-zero decimal places that do not end and do not have a repeating sequence. The "do not end" part is what bothers me about pi. Consider that we normally measure rotation in angular units of radians, and that 2π radians is defined as one full rotation. If we never had to count more than a single rotation, then stopping at something other than an inexact number is not so bothersome... although it actually is bothersome since the rotation stops exactly at some angle even if it cannot be measured in terms of pi. It doesn't asymptotically approach a exactly quarter of a turn at but never actually stops. Rotation can stop at exactly a quarter turn (exactly 90°) even if π/2 radians itself is inexact. Rotation can stop at exactly half a turn (exactly 180°) even if π radians itself is inexact. That just doesn't seem right, does it?

To really make the point, progress thorough a full rotation. At some point the first full rotation is exactly completed and the next rotation ensues. We routinely equate exactly 2π radians (an irrational number) with 360° (a rational number). How can an irrational number like π radians be exactly equal to a rational number like 180°? Does assigning the angle unit of "radian" magically make it rational? The concept seems... irrational.

Mathematically, we are comfortable with taking the limit of a function as its variable approaches some value asymptotically, and declaring that the result can be rational. An example would be , exactly. However, we never speak of a limit when using pi to define angles. 2π radians is precisely one full rotation, π radians is exactly half a rotation, as are 360° and 180°, respectively. Do you see the logical conflict that beguiles me?

If I have a circle with a circumference of exactly 1, does that mean it does not have a diameter or radius which can be measured exactly with a sufficiently precise ruler?

Therefore, not through application of rigorous mathematical manipulations but through elementary application of reductio ad absurdum I assert that pi must in fact be rational - or at least it cannot be irrational. Maybe it is pseudorational or pseudoirrational. Either way, I boldly declare quod erat deomonstrandum (QED). Quando omni flunkus moritati (Red Green, look it up).

This article is written without doing an Internet search to see whether someone else has cogitated similarly. Surely someone has. I go out on a limb here publically demonstrating either brilliance or idiocy. If it is the latter, oh well, I've done it before and I'll consider it further confirmation that I am, myself, irrational. If it is the former, then feel free to nominate me for the Nobel Prize in mathematics for having proved that pi is rational after all.

Update: I posted this proposition on LinkedIn and have received a few comments. It's probably not allowed to copy them here, so I'll just post my reply to the opinions:

****

Thanks again for the comments. My primary point is that it makes no sense to equate an irrational value like 2 pi radians to a rational number like 360 degrees, which is what we routinely do. According to Merriam Webster, a radian is "a unit of plane angular measurement that is equal to the angle at the center of a circle subtended by an arc equal in length to the radius." A degree is "a 360th part of the circumference of a circle." So, you can rotate exactly 360 degrees to complete exactly one full rotation since a degree is defined as exactly 1/360th of a rotation, thus closing the circle. Can you also rotate exactly 2 pi radians and complete exactly one full rotation since a radian is defined by what always works out to be an imprecise, irrational value? For any arbitrarily minute, exact step size you can increment exactly from   360 minus [step size]   degrees to a full circle by adding one [step size] degrees. Can you do the same exact sort of operation using pi and radians? Using pi and radians means you can only close the circle after reaching the last digit in pi, which if pi is an irrational number, can never be reached. Is there another set of values, not related to pi, where we exactly equate a rational number to an irrational number? (8/2/2012)

Posted February 6, 2024
(updated from original post on 7/21/2012)