Calculation of Energy Used by Weight-Driven Clock Movement

How much energy does it take to power a pendulum-regulated, gravity-driven mechanical clock for a full day? I decided to use my hand-crafted grandmother clock as a test bed. Three 5-pound lead weights provide motivation for countering the friction of all the gears and chime hammers. Calculation of the energy consumption is a Physics 101 problem since the familiar governing equation is that of potential energy in the Earth's gravitational field:

All three weights were reset to the top of the travel and a reference measurement was made (see photo). All three weights drive the mechanism in unison, so they fall the same amount over time. Since I was only interested in the change in potential energy, the change of height, not the absolute height from the Earth's center, was needed. A convenient form of energy units is inch*pounds (in-lb), which is easily converted to Joules (J) and milliwatt*hours (mWh). Five consecutive days of measurements at approximately the same time (7:30 pm) resulted in the spreadsheet below.

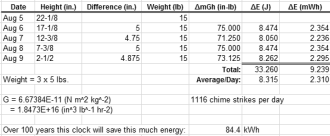
Weight drop should be the same each day, and really probably was; the reported differences are due to rounding to the nearest 1/8th inch each time. An average is given to smooth out the variation. 2.31 mWh per day is not a lot of energy considering that the weights are driving not just the clock hands, but also the hammers that strike the chimes. In fact, striking the chimes takes much more energy than driving the clock hands. It would be interesting - and I will likely do it at some point - to disable the chimes and make the same set of measurements.

At the top of each hour, this clock movement plays the familiar Westminster melody, which is a total of 16 notes. Each quarter hour it plays a cumulative 1/4 of the melody, that is at quarter past the hour it plays the first four notes, at half past the hour it plays the first eight notes, at quarter till the hour it plays the first 12 notes. So, every hour it plays 4 + 8 + 12 + 16 = 40 notes (24 x 40 = 960 per day). Then, it strikes once for each hour for 2 x (1+2+...+11+12) = 156 per day, for a grand total of 1,116 chime strikes per day - that's a lot of strikes.

Why even bother making the energy calculation? I wanted to estimate what my carbon credit should be for not drawing that energy from the electric grid. After all, most crimes short of premeditated murder can be forgiven if you can demonstrate that, especially over the last decade or two, you have made an attempt to be more green. Green holiness points are earned by driving hybrid vehicles, installing solar panels, using less toilet paper, showering less frequently, etc. Since electric power in my area of Kernersville, North Carolina, is primarily coal generated (although there is a nuclear plant over in Raleigh), it is especially important to exhibit a greener hue.

Let us assume that my clock runs for 100 years before succumbing to wear. At 2.31 mWh of energy each day and an average of 365.24 days per year, my efforts will have saved a whopping 844 kWh in a century^†. That should gain me absolution for at least an unarmed robbery. For comparison, a 23 W CFL bulb would consume 0.0231 kW * 24.0 hrs/day * (365.24 days/yr *100 yr) = 20.2E3 kWh (20.2 GWh) in the same 100 years.

† As is the custom, I will conveniently ignore the energy consumed by all the electric power tools used while building the clock

   and all the fuel used in gathering the components (wood, finishing materials, hardware).

Posted August 11, 2014