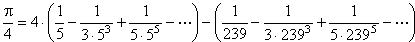Pi (π) - a Closer Look |
||
|
There are so many pages on the Internet with information on π
(pi) that I will not even attempt to outdo them. However, if you happened upon this website and are looking for
series expansions for calculating π, then you have come to the
right place. Here are a few of the most popular. The earliest renditions of π resulted from estimating the relationship of measurements of the circumference of a circle to its diameter. Here are a few early values, which were all ratios of whole numbers because at the time it was inconceivable that something "irrational" could exist:
which is the first infinite series ever found for π, by James Gregory (1638-1675). The problem is that this series (called the Gregory-Leibniz series) converges very slowly on π: 300 terms are needed to be accurate to only two decimal places! Newton (1656-1742) had a better idea (many, actually) and discovered the following: 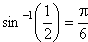 , then , then
He then determined that
Another series by Gregory was produced using two arctangents which resulted in:
Euler (1707-1783) determined that
This series by David and Gregory Chudnovsky of Columbia University produced over 4 billion digits in 1994, and each term gives an additional 14 digits: 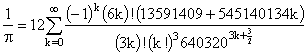
The incredibly simple series here was recently discovered:
...and was used as the basis for a handy algorithm that produces any digit of π one might desire, albeit in hexadecimal - see Reference 2, below, for the formula (too much involved to repeat it here). (thanks to Hugo K. for these last three items and for Reference 2, below) 2. "The Quest for Pi" by David H. Bailey, Jonathan M. Borwein, Peter B. Borwein and Simon
Plouffe |
||
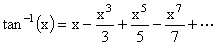 and since
and since