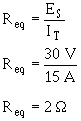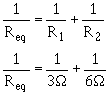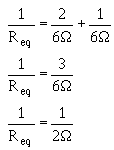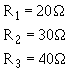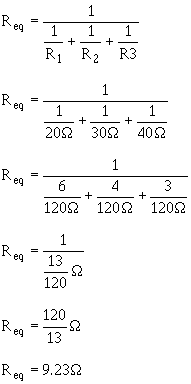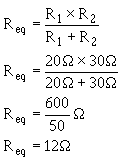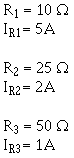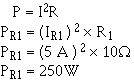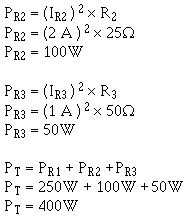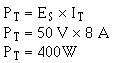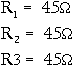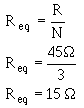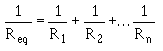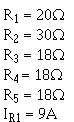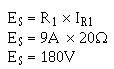Module 1 - Introduction to Matter, Energy, and Direct Current |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Module 1 − Introduction to Matter, Energy, and Direct Current
Pages i, 1−1, 1−11, 1−21, 1−31, 1−41, 1−51, 1−61, 2−1, 2−11, 2−21, 3−1, 3−11, 3−21, 3−31, 3−41, 3−51, 3−61, 3−71, 3−81, 3−91, 3−101, 3−111, 3−121, Appendix I, II, III, IV, V, Index
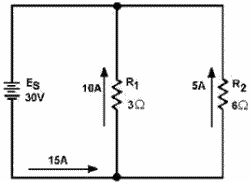
Figure 3-45. - Example circuit with unequal parallel resistors. Given:
Solution:
The equivalent resistance the circuit shown in figure 3-45 is smaller than either the two resistors (R1, R2). An important point to remember is that the equivalent resistance a parallel circuit is always less than the resistance any branch. Equivalent resistance can be found if you know the individual resistance values and the source voltage. By calculating each branch current, adding the branch currents to calculate total current, and dividing the source voltage by the total current, the total can be found. This method, while effective, is somewhat lengthy. a quicker method finding equivalent resistance is to use the general formula for resistors in parallel:
If you apply the general formula to the circuit shown in figure 3-45 you will get the same value for equivalent resistance (2 ) as was obtained in the previous calculation that used source voltage and total current.
3-61 Given:
Solution:
Convert the fractions to a common denominator.
Since both sides are reciprocals (divided into one), disregard the reciprocal function.
The formula you were given for equal resistors in parallel
is a simplification the general formula for resistors in parallel
There are other simplifications the general formula for resistors in parallel which can be used to calculate the total or equivalent resistance in a parallel circuit. RECIPROCAL METHOD. - This method is based upon taking the reciprocal each side the equation. This presents the general formula for resistors in parallel as:
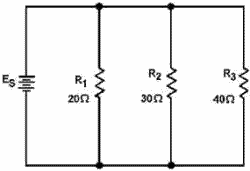
3-62 This formula is used to solve for the equivalent resistance a number unequal parallel resistors. You must find the lowest common denominator in solving these problems. If you are a little hazy on finding the lowest common denominator, brush up on it in Mathematics Volume 1, NAVEDTRA 10069 (Series). Example: Three resistors are connected in parallel as shown in figure 3-46. The resistor values are: R1 = 20 ohms, R2 = 30 ohms, R3 = 40 ohms. What is the equivalent resistance? (Use the reciprocal method.)
Figure 3-46. - Example parallel circuit with unequal branch resistors. Given:
3-63 Solution:
Product OVER The SUM METHOD. - a convenient method for finding the equivalent, or total, resistance two parallel resistors is by using the following formula.
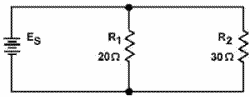
This equation, called the product over the sum formula, is used so frequently it should be committed to memory. Example: What is the equivalent resistance a 20-ohm and a 30-ohm resistor connected in parallel, as in figure 3-47?
Figure 3-47. - Parallel circuit with two unequal resistors.
3-64 Given:
Solution:
Q36. Four equal resistors are connected in parallel, each resistor has an ohmic value 100 ohms, what is the equivalent resistance? Q37. Three resistors connected in parallel have values 12 k , 20 k , and 30 k What is the equivalent resistance? Q38. Two resistors connected in parallel have values 10 k and 30 k What is the equivalent resistance? Power in a Parallel Circuit Power computations in a parallel circuit are essentially the same as those used for the series circuit. Since power dissipation in resistors consists a heat loss, power dissipations are additive regardless how the resistors are connected in the circuit. The total power is equal to the sum the power dissipated by the individual resistors. Like the series circuit, the total power consumed by the parallel circuit is:
Example: Find the total power consumed by the circuit in figure 3-48.
3-65
Figure 3-48. - Example parallel circuit. Given:
Solution:
3-66
Since the total current and source voltage are known, the total power can also be computed by: Given:
Solution:
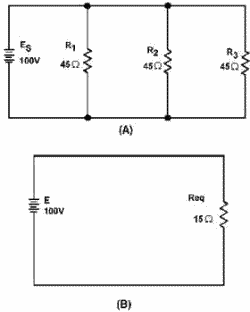
Equivalent Circuits In the study electricity, it is ten necessary to reduce a complex circuit into a simpler form. Any complex circuit consisting resistances can be redrawn (reduced) to a basic equivalent circuit containing the voltage source and a single resistor representing total resistance. This process is called reduction to an EQUIVALENT Circuit. Figure 3-49 shows a parallel circuit with three resistors equal value and the redrawn equivalent circuit. The parallel circuit shown in part a shows the original circuit. To create the equivalent circuit, you must first calculate the equivalent resistance.
3-67
Figure 3-49. - Parallel circuit with equivalent circuit. Given:
Solution:
Once the equivalent resistance is known, a new circuit is drawn consisting a single resistor (to represent the equivalent resistance) and the voltage source, as shown in part B. Rules for Parallel DC Circuits 1. The same voltage exists across each branch a parallel circuit and is equal to the source voltage.
3-68 2. The current through a branch a parallel network is inversely proportional to the amount resistance the branch. 3. The total current a parallel circuit is equal to the sum the individual branch currents the circuit. 4. The total resistance a parallel circuit is found by the general formula:
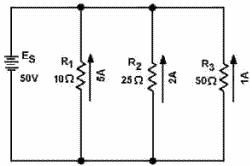
or one the formulas derived from this general formula. 5. The total power consumed in a parallel circuit is equal to the sum the power consumptions the individual resistances. SOLVING PARALLEL Circuit PROBLEMS Problems involving the determination resistance, voltage, current, and power in a parallel circuit are solved as simply as in a series circuit. The procedure is the same - (1) draw the circuit diagram, (2) state the values given and the values to be found, (3) select the equations to be used in solving for the unknown quantities based upon the known quantities, and (4) substitute the known values in the equation you have selected and solve for the unknown value. Example: a parallel circuit consists five resistors. The value each resistor is known and the current through R1 is known. You are asked to calculate the value for total resistance, total power, total current, source voltage, the power used by each resistor, and the current through resistors R2, R3, R4, and R5. Given:
Find:
This may appear to be a large amount mathematical manipulation. However, if you use the step- by-step approach, the circuit will fall apart quite easily. The first step in solving this problem is for you to draw the circuit and indicate the known values as shown in figure 3-50.
3-69
Figure 3-50. - Parallel circuit problem. There are several ways to approach this problem. With the values you have been given, you could first solve for RT, the power used by R1, or the voltage across R1, which you know is equal to the source voltage and the voltage across each the other resistors. Solving for RT or the power used by Ri will not help in solving for the other unknown values. Once the voltage across R1 is known, this value will help you calculate other unknowns. Therefore the logical unknown to solve for is the source voltage (the voltage across R1). Given:
Solution:
Now that source voltage is known, you can solve for current in each branch. Given:
3-70
|
||||||||||||||||||||||||||||||||||||||||||||||||||