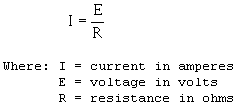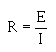Module 1 - Introduction to Matter, Energy, and Direct Current |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Module 1 − Introduction to Matter, Energy, and Direct Current
Pages i, 1−1, 1−11, 1−21, 1−31, 1−41, 1−51, 1−61, 2−1, 2−11, 2−21, 3−1, 3−11, 3−21, 3−31, 3−41, 3−51, 3−61, 3−71, 3−81, 3−91, 3−101, 3−111, 3−121, Appendix I, II, III, IV, V, Index
Chapter 3 Direct CURRENT Learning Objectives Upon completing this chapter, you will be able to: 1. Identify the term schematic diagram and identify the components in a circuit from a simple schematic diagram. 2. State the equation for Ohm's law and describe the effects on current caused by changes in a circuit. 3. Given simple graphs current versus power and voltage versus power, determine the value circuit power for a given current and voltage. 4. Identify the term power, and state three formulas for computing power. 5. Compute circuit and component power in series, parallel, and combination circuits. 6. Compute the efficiency an electrical device. 7. Solve for unknown quantities resistance, current, and voltage in a series circuit. 8. Describe how voltage polarities are assigned to the voltage drops across resistors when Kirchhoff's voltage law is used. 9. State the voltage at the reference point in a circuit. 10. Define open and short circuits and describe their effects on a circuit. 11. State the meaning the term source resistance and describe its effect on a circuit. 12. Describe in terms circuit values the circuit condition needed for maximum power transfer. 13. Compute efficiency power transfer in a circuit. 14. Solve for unknown quantities resistance, current, and voltage in a parallel circuit. 15. State the significance the polarity assigned to a current when using Kirchhoff's current law. 16. State the meaning the term equivalent resistance. 17. Compute resistance, current, voltage, and power in voltage dividers. 18. Describe the method by which a single voltage divider can provide both positive and negative voltages. 19. Recognize the safety precautions associated with the hazard electrical shock. 20. Identify the first aid procedures for a victim electrical shock.
3-1 Introduction The material covered in this chapter contains many new terms that are explained as you progress through the material. The basic dc circuit is the easiest to understand, so the chapter begins with the basic circuit and from there works into the basic schematic diagram that circuit. The schematic diagram is used in all your future work in electricity and electronics. It is very important that you become familiar with the symbols that are used. This chapter also explains how to determine the total resistance, current, voltage, and power in a series, parallel, or combination circuit through the use Ohm's and Kirchhoff's laws. The voltage divider network, series, parallel, and series-parallel practice problem circuits will be used for practical examples what you have learned. The Basic ELECTRIC Circuit The flashlight is an example a basic electric circuit. It contains a source electrical energy (the dry cells in the flashlight), a load (the bulb) which changes the electrical energy into a more useful form energy (light), and a switch to control the energy delivered to the load. Before you study a schematic representation the flashlight, it is necessary to define certain terms. The Load is any device through which an electrical current flows and which changes this electrical energy into a more useful form. Some common examples loads are a light bulb, which changes electrical energy to light energy; an electric motor, which changes electrical energy into mechanical energy; and the speaker in a radio, which changes electrical energy into sound. The SOURCE is the device which furnishes the electrical energy used by the load. It may consist a simple dry cell (as in a flashlight), a storage battery (as in an automobile), or a power supply (such as a battery charger). The Switch, which permits control the electrical device, interrupts the current delivered to the load.
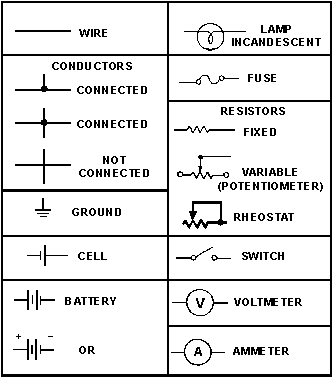
3-2 SCHEMATIC REPRESENTATION The technician's main aid in troubleshooting a circuit in a piece equipment is the SCHEMATIC Diagram. The schematic diagram is a "picture" the circuit that uses symbols to represent the various circuit components; physically large or complex circuits can be shown on a relatively small diagram. Before studying the basic schematic, look at figure 3-1. This figure shows the symbols that are used in this chapter. These, and others like them, are referred to and used throughout the study electricity and electronics.
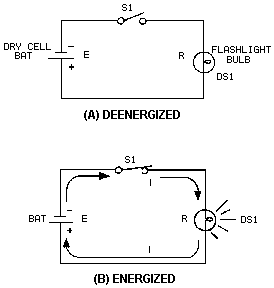
Figure 3-1. - Symbols commonly used in electricity. The schematic in figure 3-2 represents a flashlight. View a the figure shows the flashlight in the f or deenergized state. The switch (Si) is open. There is no complete path for current (I) through the circuit, and the bulb (DSi) does not light. In figure 3-2 view B, switch Si is closed. Current flows in the direction the arrows from the negative terminal the battery (BAT), through the switch (Si), through the lamp (DSi), and back to the positive terminal the battery. With the switch closed the path for current is complete. Current will continue to flow until the switch (Si) is moved to the open position or the battery is completely discharged.
3-3
Figure 3-2. - Basic flashlight schematic. Q1. In figure 3-2, what part the circuit is the (a) load and (b) source? Q2. What happens to the path for current when Si is open as shown in figure 3-2(A)? Q3. What is the name given to the "picture" a circuit such as the one shown in figure 3-2? OHM'S LAW In the early part the 19th century, George Simon Ohm proved by experiment that a precise relationship exists between current, voltage, and resistance. This relationship is called Ohm's law and is stated as follows: The current in a circuit is DirectLY proportional to the applied voltage and INVERSELY proportional to the circuit resistance. Ohm's law may be expressed as an equation:
As stated in Ohm's law, current is inversely proportional to resistance. This means, as the resistance in a circuit increases, the current decreases proportionately.
3-4 In the equation
if any two quantities are known, the third one can be determined. Refer to figure 3-2(B), the schematic the flashlight. If the battery (BAT) supplies a voltage 1.5 volts and the lamp (DS1) has a resistance 5 ohms, then the current in the circuit can be determined. Using this equation and substituting values:
If the flashlight were a two-cell flashlight, we would have twice the voltage, or 3.0 volts, applied to the circuit. Using this voltage in the equation:
You can see that the current has doubled as the voltage has doubled. This demonstrates that the current is directly proportional to the applied voltage. If the value resistance the lamp is doubled, the equation will be:
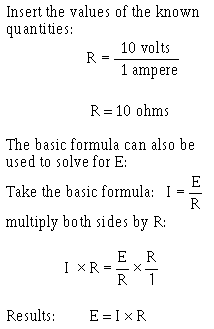
The current has been reduced to one half the value the previous equation, or .3 ampere. This demonstrates that the current is inversely proportional to the resistance. Doubling the value the resistance the load reduces circuit current value to one half its former value. APPLICATION OHM'S LAW By using Ohm's law, you are able to find the resistance a circuit, knowing only the voltage and the current in the circuit. In any equation, if all the variables (parameters) are known except one, that unknown can be found. For example, using Ohm's law, if current (I) and voltage (E) are known, resistance (R) the only parameter not known, can be determined: 1. Basic formula:
2. Remove the divisor by multiplying both sides by R:
3-5
3. Result step 2: R x I = E 4. To get R alone (on one side the equation) divide both sides by I:
5. The basic formula, transposed for R, is:
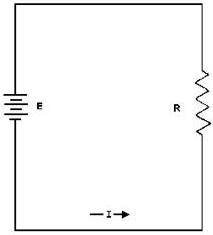
Refer to figure 3-3 where E equals 10 volts and I equals 1 ampere. Solve for R, using the equation just explained. Given: E = 10 volts I = 1 ampere Solution:
Figure 3-3. - Determining resistance in a basic circuit.
3-6
This equation can be used to find the voltage for the circuit shown in figure 3-4.
Figure 3-4. - Determining voltage in a basic circuit.
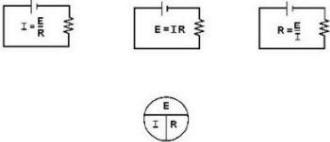
3-7 The Ohm's law equation and its various forms may be obtained readily with the aid figure 3-5. The circle containing E, I, and R is divided into two parts, with E above the line and with I and R below the line. To determine the unknown quantity, first cover that quantity with a finger. The position the uncovered letters in the circle will indicate the mathematical operation to be performed. For example, to find I, cover I with a finger. The uncovered letters indicate that E is to be divided by R, or
To find the formula for E, cover E with your finger. The result indicates that I is to be multiplied by R, or E = IR. To find the formula for R, cover R. The result indicates that E is to be divided by I, or
Figure 3-5. - Ohm's law in diagram form. You are cautioned not to rely wholly on the use this diagram when you transpose the Ohm's law formulas. The diagram should be used to supplement your knowledge the algebraic method. Algebra is a basic tool in the solution electrical problems. Q4. According to Ohm's law, what happens to circuit current if the applied voltage (a) increases, (b) decreases? Q5. According to Ohm's law, what happens to circuit current if circuit resistance (a) increases, (b) decreases? Q6. What is the equation used to find circuit resistance if voltage and current values are known? GRAPHICAL ANALYSIs The Basic Circuit One the most valuable methods analyzing a circuit is by constructing a graph. No other method provides a more convenient or more rapid way to observe the characteristics an electrical device.
3-8 The first step in constructing a graph is to obtain a table data. The information in the table can be obtained by taking measurements on the circuit under examination, or can be obtained theoretically through a series Ohm's law computations. The latter method is used here. Since there are three variables (E, I, and R) to be analyzed, there are three distinct graphs that may be constructed. To construct any graph electrical quantities, it is standard practice to vary one quantity in a specified way and note the changes which occur in a second quantity. The quantity which is intentionally varied is called the independent variable and is plotted on the horizontal axis. The horizontal axis is known as the X-AXIs. The second quantity, which varies as a result changes in the first quantity, is called the dependent variable and is plotted on the vertical, or Y-AXIs. Any other quantities involved are held constant. For example, in the circuit shown in figure 3-6, if the resistance was held at 10 ohms and the voltage was varied, the resulting changes in current could then be graphed. The resistance is the constant, the voltage is the independent variable, and the current is the dependent variable.
Figure 3-6. - Three variables in a basic circuit. Figure 3-7 shows the graph and a table values. This table shows R held constant at 10 ohms as E is varied from 0 to 20 volts in 5-volt steps. Through the use Ohm's law, you can calculate the value current for each value voltage shown in the table. When the table is complete, the information it contains can be used to construct the graph shown in figure 3-7. For example, when the voltage applied to the 10-ohm resistor is 10 volts, the current is 1 ampere. These values current and voltage determine a point on the graph. When all five points have been plotted, a smooth curve is drawn through the points.
3-9
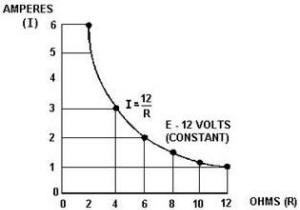
Figure 3-7. - Volt-ampere characteristic. Through the use this curve, the value current through the resistor can be quickly determined for any value voltage between 0 and 20 volts. Since the curve is a straight line, it shows that equal changes voltage across the resistor produce equal changes in current through the resistor. This fact illustrates an important characteristic the basic law - the current varies directly with the applied voltage when the resistance is held constant. When the voltage across a load is held constant, the current depends solely upon the resistance the load. For example, figure 3-8 shows a graph with the voltage held constant at 12 volts. The independent variable is the resistance which is varied from 2 ohms to 12 ohms. The current is the dependent variable. Values for current can be calculated as:
3-10
|
||||||||||||||||||||||||||||||||||||||||||||||||||