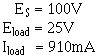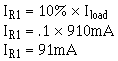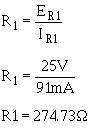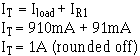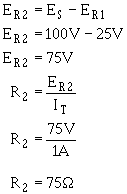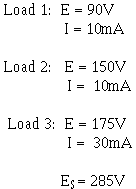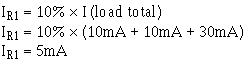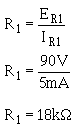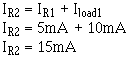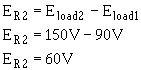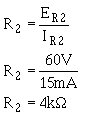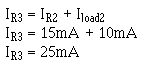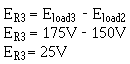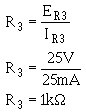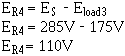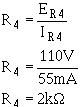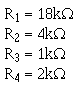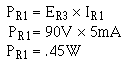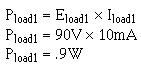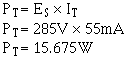Module 1 - Introduction to Matter, Energy, and Direct Current |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Module 1 − Introduction to Matter, Energy, and Direct Current
Pages i, 1−1, 1−11, 1−21, 1−31, 1−41, 1−51, 1−61, 2−1, 2−11, 2−21, 3−1, 3−11, 3−21, 3−31, 3−41, 3−51, 3−61, 3−71, 3−81, 3−91, 3−101, 3−111, 3−121, Appendix I, II, III, IV, V, Index
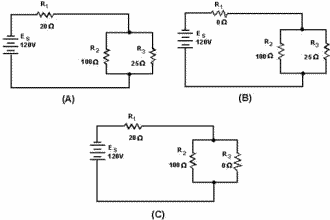
circuit involved. To illustrate this point, figure 3-62 shows a series-parallel network in which shorts are developed. In figure 3-62 (A) the normal circuit is shown. RT = 40 ohms and IT = 3 amps.
Figure 3-62. - Series-parallel circuit with shorts. In figure 3-62 (B), R1 has shorted. R1 now has zero ohms resistance. The total the resistance the circuit is now equal to the resistance the parallel network R2 and R3, or 20 ohms. Circuit current has increased to 6 amps. All this current goes through the parallel network (R2, R3) and this increase in current would most likely damage the components. In figure 3-62 (C), R3 has shorted. With R3 shorted there is a short circuit in parallel with R2 . The short circuit routes the current around R2, effectively removing R2 from the circuit. Total circuit resistance is now equal to the resistance R1, or 20 ohms. As you know, R2 and R3 form a parallel network. Resistance the network can be calculated as follows: Given:
3-91 Solution:
The total circuit current with R3 shorted is 6 amps. All this current flows through R1 and would most likely damage R1. Notice that even though only one portion the parallel network was shorted, the entire paralleled network was disabled. Opens and shorts alike, if occurring in a circuit, result in an overall change in the equivalent resistance. This can cause undesirable effects in other parts the circuit due to the corresponding change in the total current flow. a short usually causes components to fail in a circuit which is not properly fused or otherwise protected. The failure may take the form a burned-out resistor, damaged source, or a fire in the circuit components and wiring. Fuses and other circuit protection devices are installed in equipment circuits to prevent damage caused by increases in current. These circuit protection devices are designed to open if current increases to a predetermined value. Circuit protection devices are connected in series with the circuit or portion the circuit that the device is protecting. When the circuit protection device opens, current flow ceases in the circuit. A more thorough explanation fuses and other circuit protection devices is presented in Module 3, Introduction to Circuit Protection, Control, and Measurement. Q46. What is the effect on total resistance and total current in a circuit if an open occurs in (a) a parallel branch, and (b) in a series portion? Q47. What is the effect on total resistance and total current in a circuit if a short occurs in (a) a parallel branch, and (b) in a series portion? Q48. If one branch a parallel network is shorted, what portion circuit current flows through the remaining branches? Voltage DIVIDERS Most electrical and electronics equipment use voltages various levels throughout their circuitry. One circuit may require a 90-volt supply, another a i50-volt supply, and still another a i80-volt supply. These voltage requirements could be supplied by three individual power sources. This method is expensive and requires a considerable amount room. The most common method supplying these voltages is to use a single voltage source and a Voltage DIVIDER. Before voltage dividers are explained, a review what was discussed earlier concerning voltage references may be help.
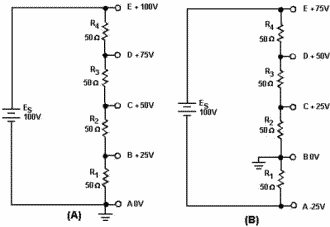
3-92 As you know, some circuits are designed to supply both positive and negative voltages. Perhaps now you wonder if a negative voltage has any less potential than a positive voltage. The answer is that 100 volts is 100 volts. Whether it is negative or positive does not affect the feeling you get when you are shocked. Voltage polarities are considered as being positive or negative in respect to a reference point, usually ground. Figure 3-63 will help to illustrate this point.
Figure 3-63. - Voltage polarities. Figure 3-63(A) shows a series circuit with a voltage source 100 volts and four 50-ohm resistors connected in series. The ground, or reference point, is connected to one end resistor R1. The current in this circuit determined by Ohm's law is .5 amp. Each resistor develops (drops) 25 volts. The five tap-f points indicated in the schematic are points at which the voltage can be measured. As indicated on the schematic, the voltage measured at each the points from point a to point E starts at zero volts and becomes more positive in 25 volt steps to a value positive 100 volts. In figure 3-63(B), the ground, or reference point has been moved to point B. The current in the circuit is still .5 amp and each resistor still develops 25 volts. The total voltage developed in the circuit remains at 100 volts, but because the reference point has been changed, the voltage at point a is negative 25 volts. Point E, which was at positive 100 volts in figure 3-63(A), now has a voltage positive 75 volts. As you can see the voltage at any point in the circuit is dependent on three factors; the current through the resistor, the ohmic value the resistor, and the reference point in the circuit. A typical voltage divider consists two or more resistors connected in series across a source voltage (Es). The source voltage must be as high or higher than any voltage developed by the voltage divider. As the source voltage is dropped in successive steps through the series resistors, any desired
3-93 portion the source voltage may be "tapped f" to supply individual voltage requirements. The values the series resistors used in the voltage divider are determined by the voltage and current requirements the loads. Figure 3-64 is used to illustrate the development a simple voltage divider. The requirement for this voltage divider is to provide a voltage 25 volts and a current 910 milliamps to the load from a source voltage 100 volts. Figure 3-64(A) provides a circuit in which 25 volts is available at point B. If the load was connected between point B and ground, you might think that the load would be supplied with 25 volts. This is not true since the load connected between point B and ground forms a parallel network the load and resistor R1. (Remember that the value resistance a parallel network is always less than the value the smallest resistor in the network.)
Figure 3-64. - Simple voltage divider. Since the resistance the network would now be less than 25 ohms, the voltage at point B would be less than 25 volts. This would not satisfy the requirement the load. To determine the size resistor used in the voltage divider, a rule--thumb is used. The current in the divider resistor should equal approximately 10 percent the load current. This current, which does not flow through any the load devices, is called bleeder current. Given this information, the voltage divider can be designed using the following steps. 1. Determine the load requirement and the available voltage source.
3-94
2. Select bleeder current by applying the 10% rule--thumb.
3. Calculate bleeder resistance.
The value R1 may be rounded f to 275 ohms:
4. Calculate the total current (load plus bleeder).
5. Calculate the resistance the other divider resistor(s).
The voltage divider circuit can now be drawn as shown in figure 3-64(B). Q49. What information must be known to determine the component values for a voltage divider?
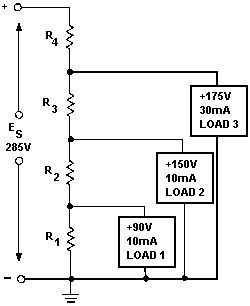
3-95 Q50. If a voltage divider is required for a load that will use 450 mA current, what should be the value bleeder current? Q51. If the load in question 50 requires a voltage +90 V, what should be the value the bleeder resistor? Q52. If the source voltage for the voltage divider in question 50 supplies 150 volts, what is the total current through the voltage divider? MULTIPLE-Load Voltage DIVIDERS A multiple-load voltage divider is shown in figure 3-65. An important point that was not emphasized before is that when using the 10% rule--thumb to calculate the bleeder current, you must take 10% the total load current.
Figure 3-65. - Multiple-load voltage divider. Given the information shown in figure 3-65, you can calculate the values for the resistors needed in the voltage-divider circuits. The same steps will be followed as in the previous voltage divider problem.
3-96 Given:
The bleeder current should be 10% the total load current. Solution:
Since the voltage across R1 (ER1) is equal to the voltage requirement for load 1, Ohm's law can be used to calculate the value for R1. Solution:
The current through R2 (IR2) is equal to the current through R1 plus the current through load 1. Solution:
The voltage across R2 (ER2) is equal to the difference between the voltage requirements load 1 and load 2.
3-97
Ohm's law can now be used to solve for the value R2 . Solution:
The current through R3 (IR3) is equal to the current through R2 plus the current through load 2.
The voltage across R3 (ER3) equals the difference between the voltage requirement load 3 and load 2.
Ohm's law can now be used to solve for the value R3 . Solution:
The current through R4 (IR4) is equal to the current through R3 plus the current through load 3. IR4 is equal to total circuit current (IT).
The voltage across R4 (ER4) equals the difference between the source voltage and the voltage requirement load 3.
3-98
Ohm's law can now be used to solve for the value R4 . Solution:
With the calculations just explained, the values the resistors used in the voltage divider are as follows:
Power IN The Voltage DIVIDER Power in the voltage divider is an extremely important quantity. The power dissipated by the resistors in the voltage divider should be calculated to determine the power handling requirements the resistors. Total power the circuit is needed to determine the power requirement the source. The power for the circuit shown in figure 3-65 is calculated as follows: Given:
Solution:
The power in each resistor is calculated just as for R1. When the calculations are performed, the following results are obtained:
3-99 To calculate the power for load 1: Given:
Solution:
The power in each load is calculated just as for load 1. When the calculations are performed, the following results are obtained.
Total power is calculated by summing the power consumed by the loads and the power dissipated by the divider resistors. The total power in the circuit is 15.675 watts. The power used by the loads and divider resistors is supplied by the source. This applies to all electrical circuits; power for all components is supplied by the source. Since power is the product voltage and current, the power supplied by the source is equal to the source voltage multiplied by the total circuit current (Es x IT). In the circuit figure 3-65, the total power can be calculated by: Given:
Solution:
Voltage DIVIDER with Positive and Negative Voltage REQUIREMENTS In many cases the load for a voltage divider requires both positive and negative voltages. Positive and negative voltages can be supplied from a single source voltage by connecting the ground (reference point) between two the divider resistors. The exact point in the circuit at which the reference point is placed depends upon the voltages required by the loads.
3-100
|
||||||||||||||||||||||||||||||||||||||||||||||||||