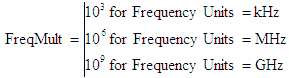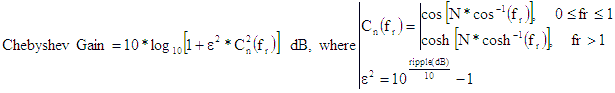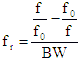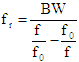RF Cascade Workbook for Excel
RF & Electronics Symbols for Visio
RF & Electronics Symbols for Office
RF & Electronics Stencils for Visio
RF Workbench
T-Shirts, Mugs, Cups, Ball Caps, Mouse Pads
Espresso Engineering Workbook™
Smith Chart™ for Excel
|
 |
RF Cascade Workbook© 2005 User's Guide - Chapter 7 |
|
Chapter
1, 2,
3, 4,
5, 6,
7, 8,
9,
10, 11,
12,
13
Version 1.11 by Kirt Blattenberger RF Cafe Website (www.rfcafe.com)
Chapter 7
7 Filter-Mixer
Worksheet
A major new feature in RF Cascade Workbook 2005 is the ability to calculate
frequency dependent parameters due to mixers and filters. System input power and inband gains for each stage
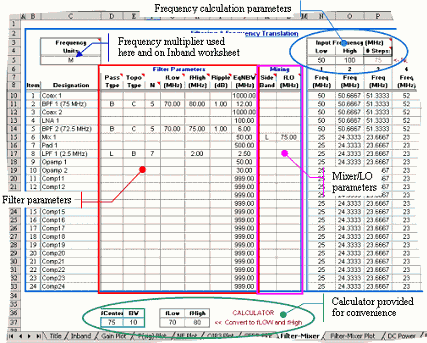
are derived from the “Input” worksheet input parameters. Min/Max values are not used here. Figure 12 shows the
parameter input area for the worksheet. By default, 75 equally spaced frequency calculation points are
provided between specified minimum and maximum frequencies, but can be changed.
Band-limiting parameters can be assigned to every stage in the cascade if you know
how to model them. In doing so, gain slope across the useful band can be modeled to predict the overall system
gain slope.
|
A low order Butterworth filer might be used with a bandwidth that results in an
inband slope that matched measured or datasheet values. Use a lowpass filter to model a negative gain slope or
a highpass filter to model a positive gain slope. Keep in mind that gain values calculated on the
“Filter-Mixer” worksheet are not used back on the “Inband” worksheet. Most users will probably only enter
specifications for filter stages. As with all simulations, the output data is only as good as the input
parameters.
Single-tone mixer intermodulation products are not calculated or included in the
output spectrum display.
|
|
|
|
Figure 12 Filter-Mixer
Input Parameter Input Area
|
|
7.1
Input Frequency
|
|
In order for Excel to calculate the frequency response, a range of frequency
values must be generated to use for the gain calculations. Furthermore, since frequency translation is
accommodate by using mixer stages, each position in the cascade must have its own frequency cell. This creates
a lot of cells and consequently a lot of calculations. A default of 75 steps is used to strike a balance
between step size, recalculation time, and file size. Parameter definitions are given in Table 4.
|
|
Parameter
|
Description
|
Range
|
Tolerance
|
Units
|
|
Low
|
Lowest input frequency to be used |
10-9 to <High
|
- |
Frequency Units
|
|
High
|
Highest input frequency to be used |
>Low to 1012
|
- |
Frequency Units
|
|
# Steps
|
Number of intervals between Low and High |
1 to 500
|
- |
- |
|
|
Table 4 Input Frequency
Parameters
|
|
If a different number of steps is required, it will be necessary to add or delete
columns in both the “Freq” and the “Psig” areas. Use the same methodology as described in section 2 for
accomplishing the changes, keeping in mind that the equations must retain their continuity.
|
|
7.2
Filters
|
|
Models are provided for the two most often-used filter transfer functions:
Butterworth and Chebyshev. If you need other response functions, you can create them simply by writing a
little VBA code or even implementing the equation directly in a range of cells.
|
|
To facilitate using filters that closely match real world filters, the orders of
the filters are not restricted to integer values. Seldom does a real 5th order Butterworth exactly match the
theoretical profile, so you can enter 4.9 or 5.1 or any other value as needed to match your actual filter.
|
|
Parameter
|
Description
|
Range
|
Tolerance
|
Units
|
Pass Type |
Lowpass, highpass, bandpass or bandstop. NOTE: Leave blank for no
filter |
“B” or “b” for Bandpass “H” or “h” for
Highpass
“L” or “l” for Lowpass “S” or “s” for bandStop
|
-
|
-
|
Topo Type |
Transfer function topology. NOTE: Leave blank for no filter |
“B” or “b” for Butterworth “C” or “c” for
Chebyshev
|
-
|
-
|
N |
Order NOTE: Leave blank for no filter |
2 to 25
|
-
|
-
|
fLow |
Lower cutoff frequency for highpass, bandpass and bandstop filters. |
10-12 to < fHigh
|
-
|
Frequency Units
|
fHigh |
Upper cutoff frequency for lowpass, bandpass and bandstop filters. |
>fLow to 1012
|
-
|
Frequency Units
|
Ripple |
Inband ripple for Chebyshev NOTE: Leave blank for no filter |
0.001 to 10
|
-
|
dB
|
EqNBW |
Equivalent noise bandwidth. This value is used on the ”Inband”
worksheet to calculate noise power levels. |
10-12 to 1012
|
-
|
Frequency Units
|
|
|
Table 5 Filter Parameters
|
|
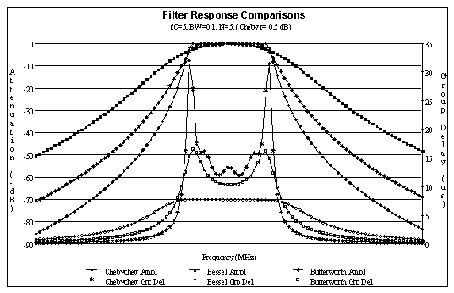
Figure 13 illustrates how three different filter topologies (Butterworth,
Chebyshev and Bessel) compare for equal order (5th). The Chebyshev filter inband ripple is arbitrarily set to
0.5 dB. Both gain and group delay are shown.
|
|
|
|
Figure 13 Bandpass Filter
Response Comparison
|
|
The following equations are the prototype functions for Butterworth and Chebyshev
filters. Use the conversions in Table 6 in place of fr for lowpass, highpass, bandpass and bandstop filter
equations. These are based on infinite “Q” implementation (purely reactive components).
|
|
Butterworth Filter
|
|
Butterworth filters are sometimes referred to as “maximally flat,” because they
exhibit the flattest passband response with no ripple. The cutoff frequency is defined at the half power point
(-3.01 dB). Only the amplitude response is used in RF Cascade Workbook.
|
|
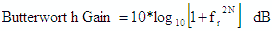
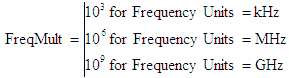
|
|
Chebyshev Filter
|
|
Chebyshev filters are sometimes referred to as “equiripple” filters because they
exhibit a ripple in the inband response. Chebyshevs have the highest out-of-band rejection for an all-pole
transfer function. Higher attenuation requires a non-monotonic out-of-band response (e.g., elliptical). Higher
inband ripple results in greater out-of-band attenuation for a fixed order number. The cutoff frequency is
defined to be where the out-of-band attenuation begins to exceed the inband ripple value.
|
|
Note that the inband ripple response is defined by a cosine function. One way to
determine the order of a lowpass or highpass Chebyshev filter is to count the number of peaks and valleys in
the inband response, which is equal to the order. For bandpass or bandstop, the order is half the number or
peaks and valleys. The out-of-band rejection is defined by a hyperbolic cosine function, which looks somewhat
like a smashed parabola (see
https://mathworld.wolfram.com/HyperbolicCosine.html), and is monotonic (no inflection points).
|
|
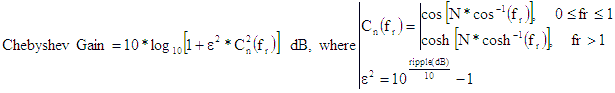
|
|
|
|
Lowpass
|
Highpass
|
Bandpass
|
Bandstop
|
|

|
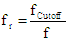
|
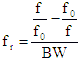
|
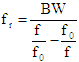
|
| |
|

|
|
|
Table 6 Filter Conversion
Factors
|
|
Chapter
1, 2,
3, 4,
5, 6,
7, 8,
9,
10, 11,
12,
13
|
Version 1.11 by Kirt Blattenberger RF Cafe Website (www.rfcafe.com)
|
Chapter 7
|
|
 |
|

 |