|
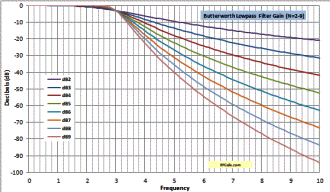
This may be the only place you will ever find the explicit formulas for Butterworth
lowpass filter gain, phase, and group delay based on the basic Butterworth
polynomials (until people copy my work and don't give
credit*). Hoping to avoid having to do the messy math of
complex numbers requiring separating out the real and imaginary parts to obtain
phase (θ) - and then to get the first derivative for group delay (τd) -
I searched high and low, far and wide for closed form equations, to no
avail. All I could
ever find was instruction to apply arg{H(ω)} for phase (θ) and -dθ/dω
for group delay -- pretty useless if you want to plug an equation into a spreadsheet
or software.
Here are
equations and plots for Butterworth highpass, bandpass, and bandstop filters.
Finally, I decided if I wanted the solutions, I would have to slog through all
the equations myself. Here is the result. The basic steps are as follow:
- Simplify the polynomial factors by multiplying out the parenthetical quantities.
- Substitute jω (or iω, but engineers use jω) for each "s," where ω is the frequency
(ωn) being evaluated divided by the cutoff frequency (ωco);
hence, jω = jωn/ωco.
- Since j2 = -1 by definition, all even powers of j result in "real"
parts and all odd powers of j result in "imaginary" parts. E.g., for 3rd-order:
- H(s) = (s + 1)(s2 + s + 1) = js3 + 2s2 +2s
+ 1
- H(jω) = (jω)3 + 2(jω)2 +2(jω) + 1 = j3ω3
+ 2(j2ω2) +2(jω) + 1
= -jω3 + 2(-ω2)
+ j2ω + 1 = -jω3 - 2ω2
+ j2ω + 1
- Re{H(jω)} =
1 - 2ω2
(parts w/o j), and Im{H(jω)} = 2ω - ω3
(parts w/j)
- Gain is G(ω) = sqrt [Re{H(jω)2 +
Im{H(jω)2]
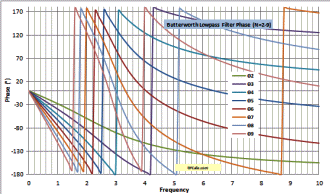
- The phase angle is by definition θ(ω) =
tan-1 (Re{H(jω)}/Im{H(jω)})
θ(ω) = tan-1 [(1 - 2ω2)
/ (2ω - ω3)]
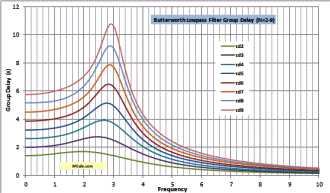
- Group delay is defined as
τd(ω)
= -dθ(ω)/dω. This is where it gets hard, mainly
due to the arctangent, but the fraction is no walk in the park, either. Fortunately,
there are online math websites like SymboLab
that will handle such derivatives. For that matter, it will multiply all the factors
for you as well, reducing the opportunity for errors.
- Finally, do the ω = ωn/ωco substitution everywhere. ωn
is the frequency at which the equation is being evaluated, and ωco is
the cutoff frequency. Frequency units cancel out, so a 1 Hz cutoff plots the
same as a 1 kHz cutoff or a 1 GHz cutoff for gain and phase. The group delay
scale needs to be divided by a factor equal to the frequency units (÷103
for kHz, ÷106 for MHz, etc.).
This table represents hours of work on my part. I will eventually get around
to lowpass, highpass, bandpass, and bandreject for Butterworth, Chebyshev, and Bessel
(and maybe Gaussian) filters.
Butterworth Lowpass, Highpass, Bandpass, and Bandstop Filter Calculator with Gain, Phase and Group Delay
are
now part of my free
RF Cafe Espresso Engineering Workbook™!
* I had
Archive.org save a copy of this page in order to prove this
is my original work.
| N |
|
| 1 |
|
s + 1
(jω) + 1
sqrt (1 + ω2)
|
|
tan-1 (1/ω)
|
|
1/(1 + ω2)
|
|
| 2 |
|
s2 + 1 + 1.4142s
(jω)2 + 1.4142(jω) + 1
(1 - ω2) + j1.4142ω
sqrt [(1 - ω2)2 + (1.4142ω)2]
|
|
tan-1 [(1 - ω2)/1.4142ω]
|
|
(1 + ω2)/[1.4142(0.5ω4 - 0.0001ω2) + 0.5]
|
|
| 3 |
|
s3 + 2s2 + 2s + 1
(jω)3 + 2(jω)2
+ 2(jω) + 1
(1 - 2ω2) + j(2ω - ω3)
sqrt [(1 - 2ω2)2
+ (2ω - ω3)2]
|
|
tan-1 [(1 - 2*ω2)/(2ω - ω3)]
|
|
(2*ω4 + ω2 + 2)/(ω6 + 1)
|
|
| 4 |
|
s4 + 2.6131s3 + 3.4142s2 + 2.6131s + 1
(jω)4 + 2.6131(jω)3 + 3.4142(jω)2 + 2.6131(jω)
+ 1
(ω4 - 3.4142ω2 + 1) + j(-2.6131ω3 + 2.6131ω)
sqrt [(ω4 - 3.4142ω2 + 1)2 + (-2.6131ω3
+ 2.6131ω)2]
|
| tan-1 [(ω4 - 3.4142ω2 + 1)/(-2.6131ω3
+ 2.6131ω)] |
| (2.6131ω6 + 1.08234602ω4 + 1.08234602ω2 + 2.6131)
/ (ω8 - 0.00010839ω6 + 0.00017842ω4 - 0.00010839ω2
+ 1) |
|
| 5 |
|
s5 + 3.2361s4 + 5.2361s3 + 5.2361s2
+ 3.2361s + 1
(jω)5 + 3.2361(jω)4 + 5.2361(jω)3 + 5.2361(jω)2
+ 3.2361(jω) + 1
(3.2361ω4 - 5.2361ω2+1) + j(ω5 - 5.2361ω3
+ 3.2361ω)
sqrt [(3.2361ω4 - 5.2361ω2 + 1)2 + (ω5
- 5.2361ω3 + 3.2361ω)2]
|
| tan-1 [(3.2361ω4 - 5.2361ω2 + 1)/(ω5
- 5.2361ω3 + 3.2361ω)] |
| (3.2361ω8 + 1.23624321ω6 + 0.99971358ω4 + 1.23624321ω2
+ 3.2361) / (ω10 + 0.00014321ω8 - 0.00014321ω6
- 0.00014321ω4 + 0.00014321ω2 + 1) |
|
| 6 |
|
s6 + 3.8637s5 + 7.4641s4 + 9.1416s3
+ 7.4641s2 + 3.8637s + 1
(jω)6 + 3.8637(jω)5 + 7.4641(jω)4 + 9.1416(jω)3
+ 7.4641(jω)2 + 3.8637(jω) + 1
(-ω6 + 7.4641ω4 - 7.4641ω2 + 1) + j(3.8637ω5
- 9.1416ω3 + 3.8637ω)
sqrt [(-ω6 + 7.4641ω4 - 7.4641ω2 + 1)2
+ (3.8637ω5 - 9.1416ω3 + 3.8637ω)2]
|
|
tan-1 [(-ω6 + 7.4641ω4 - 7.4641ω2
+ 1)/(3.8637ω5 - 9.1416ω3 + 3.8637ω)]
|
|
(3.8637*ω10 + 1.41424317*ω8 + 1.03518705*ω6
+ 1.03518705*ω4 + 1.41424317*ω2 + 3.8637) / (ω12
- 0.00002231*ω10 + 0.00018897*ω8 - 0.00037168*ω6
+ 0.00018897*ω4 - 0.00002231*ω2 + 1)
|
|
| 7 |
|
s7 + 4.4940s6 + 10.0978s5 + 14.5920s4
+ 14.5920s3 + 10.0978s2 + 4.4940s + 1
(jω)7 + 4.4940(jω)6 + 10.0978(jω)5 + 14.5920(jω)4
+ 14.5920(jω)3 + 10.0978(jω)2 + 4.4940(jω) + 1
(-4.494ω6 + 14.592ω4 - 10.0978ω2 + 1) + j(-ω7
+ 10.0978ω5 - 14.592ω3 + 4.494ω)
sqrt [(-4.494ω6 + 14.592ω4 - 10.0978ω2 + 1)2
+ (-ω7 + 10.0978ω5 - 14.592ω3 + 4.494ω)2]
|
| tan-1 [(-4.494ω6 + 14.592ω4 - 10.0978ω2
+ 1)/(-ω7 + 10.0978ω5 - 14.592ω3 + 4.494ω)] |
|
(4.494ω12 + 1.6035132ω10 + 1.1067536ω8 + 1.00994948ω6
+ 1.1067536ω4 + 1.6035132ω2 + 4.494) / (ω14+0.000436ω12
- 0.00333116ω10 + 0.0032952ω8 + 0.0032952ω6-0.00333116ω4
+ 0.000436ω2 + 1)
|
|
| 8 |
|
s8 + 5.1528s7 + 13.1371s6 + 21.8462s5
+ 25.6884s4 + 21.8462s3 + 13.1371s2 + 5.1528s + 1
(jω)8 + 5.1258(jω)7 + 13.1371(jω)6 + 21.8462(jω)5
+ 25.6884(jω)4 + 21.8462(jω)3 + 13.1371(jω)2 +
5.1258(jω) + 1
(ω8 - 13.1371ω6 + 25.6884ω4 - 13.1371ω2
+ 1) + j(-5.1258ω7 + 21.8462ω5 - 21.8462ω3 + 5.1258ω)
|
|
tan-1 [(ω8 - 13.1371ω6 + 25.6884ω4
- 13.1371ω2 + 1)/(-5.1258ω7 + 21.8462ω5 - 21.8462ω3
+ 5.1258ω)]
|
|
(5.1258ω14 + 1.79954718ω12 + 1.20591186ω10 +
1.01691792ω8 + 1.01691792ω6 - 1.20591186ω4 + 1.79954718ω2
+ 5.1258) / (ω16 - 0.00037436ω14 + 0.00169249ω12
- 0.00140092ω10 + 0.00012722ω8 - 0.00140092ω6 +
0.00169249ω4 - 0.00037436ω2 + 1)
|
|
| 9 |
|
ω9 + 5.7588ω8 + 16.5817ω7 + 31.1634ω6
+ 41.9864ω5 + 41.9864ω4 + 31.1634ω3 + 16.5817ω2
+ 5.7588ω + 1
(jω)9 + 5.7588(jω)8 + 16.5817(jω)7 + 31.1634(jω)6
+ 41.9864(jω)5 + 41.9864(jω)4 + 31.1634(jω)3 +
16.5817(jω)2 + 5.7588(jω) + 1
(5.7588ω8 - 31.1634ω6 + 41.9864ω4 - 16.5817ω2
+ 1) + j(ω9 - 16.5817ω 7 + 41.9864ω5 - 31.1634ω3
+ 5.7588ω)
sqrt [(5.7588ω8 - 31.1634ω6 + 41.9864ω4 - 16.5817ω2
+ 1)2 + (ω9 - 16.5817ω 7 + 41.9864ω5
- 31.1634ω3 + 5.7588ω)2]
|
|
tan-1 [(5.7588ω8 - 31.1634ω6 + 41.9864ω4
- 16.5817ω2 + 1)/(ω9 - 16.5817ω 7 + 41.9864ω5
- 31.1634ω3 + 5.7588ω)]
|
|
(5.7588ω16 + 2.00049396ω14 + 1.30030882ω12 +
1.06835072ω10 + 1.00271865ω8 + 1.06835072ω6 + 1.30030882ω4
+ 2.00049396ω2 + 5.7588) / (ω18 + 0.00037744ω16
- 0.00200095ω14 + 0.00148244ω12 + 0.00034108ω10
+ 0.00034108ω8 + 0.00148244ω6 - 0.00200095ω4 +
0.00037744ω2 + 1)
|
|
Posted December 1, 2023
|