|
|
|||||||||
| Software: RF Cascade Workbook | RF Symbols for Office | RF Symbols & Stencils for Visio | Espresso Workbook | ||||||||||
|
|||||||||||||||||||||||||||||||
   |
   |
||||||||||||||||||||||||||||||
|
Please Support RF Cafe by purchasing my ridiculously low-priced products, all of which I created. RF & Electronics Symbols for Visio RF & Electronics Symbols for Office RF & Electronics Stencils for Visio T-Shirts, Mugs, Cups, Ball Caps, Mouse Pads These Are Available for Free |
|||||||||||||||||||||||||||||||
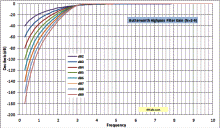
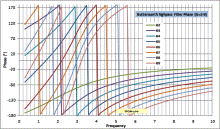
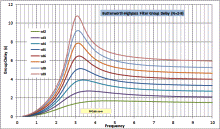
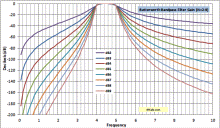
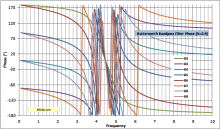
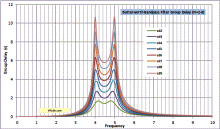
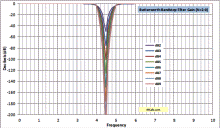
Butterworth Highpass & Bandpass Filter Gain, Phase, and Group Delay Equations
A few days ago I posted a webpage detailing my work to generate equations for gain, phase, and group delay for a Butterworth lowpass filter, using the basic polynomials. I could not find them anywhere on the Web or in filter design books I own. The only difference between calculating Butterworth lowpass, highpass, bandpass, and bandstop filter values for gain, phase, and group delay is how the relative frequency is defined. Simply substitute the following for ω in any of the equations for gain, phase, or group delay. It's that simple. Graphs are published below. Frequency units cancel out, so a 1 Hz cutoff plots the same as a 1 kHz cutoff or a 1 GHz cutoff for gain and phase. The group delay scale needs to be divided by a factor equal to the frequency units (÷103 for kHz, ÷106 for MHz, etc.).
Butterworth Lowpass, Highpass, Bandpass, and Bandstop Filter Calculator with Gain, Phase and Group Delay are now part of my free RF Cafe Espresso Engineering Workbook™!
|
Lowpass ω = ωn/ωco Where ωn is the frequency at which the equation is being evaluated, and ωco is the cutoff frequency |
Highpass ω = ωco/ωn Where ωn is the frequency at which the equation is being evaluated, and ωco is the cutoff frequency |
Bandpass ω = (ωn/ω0 - ω0/ωn) / BW ω0 = sqrt (ωU * ωL) BW = (ωU - ωL) / ω0 Where ωn is the frequency at which the equation is being evaluated, ω0 is the geometric average center frequency, ωU is the upper cutoff frequency, and ωL is the lower cutoff frequency. |
Bandstop ω = BW / (ωn/ω0 - ω0/ωn) ω0 = sqrt (ωU * ωL) BW = (ωU - ωL) / ω0
Where ωn is the frequency at which the equation is being evaluated, ω0 is the geometric average center frequency, ωU is the upper cutoff frequency, and ωL is the lower cutoff frequency. |
I had Archive.org save a copy of this page in order to prove this is my original work.
|
Butterworth Highpass Filter
Gain
Phase
Group Delay |
Butterworth Bandpass Filter
Gain
Phase
Group Delay |
Butterworth Bandstop Filter
Gain
Phase
Group Delay |
Posted December 13, 2023
Related Pages on RF Cafe
- Butterworth Filter Equations for Magnitude, Phase, and Group Delay
- Chebyshev Filter Equations for Magnitude, Phase, and Group Delay
- Butterworth Lowpass Filter Gain, Phase, and Group Delay Equations
- Butterworth Highpass, Bandpass, & Bandstop Filter Gain, Phase, and Group Delay Equations
- How to Use Filter Equations in a Spreadsheet
- Filter Equivalent Noise Bandwidth
- Filter Prototype Denormalization
- Bessel Filter Prototype Element Values
- Butterworth Lowpass Filter Poles
- Butterworth Filter Prototype Element Values
- Chebyshev Lowpass Filter Poles
- Chebyshev Filter Prototype Element Values
- Monolithic Ceramic Block Combline Bandpass Filters Design
- Coupled Microstrip Filters: Simple Methodologies for Improved Characteristics
Copyright: 1996 - 2026 |
About RF Cafe RF Cafe began life in 1996 as "RF Tools" in an AOL screen name web space totaling 2 MB. Its primary purpose was to provide me with ready access to commonly needed formulas and reference material while performing my work as an RF system and circuit design engineer. The World Wide Web (Internet) was largely an unknown entity at the time and bandwidth was a scarce commodity. Dial-up modems blazed along at 14.4 kbps while tying up your telephone line, and a lady's voice announced "You've Got Mail" when a new message arrived... |
Copyright 1996 - 2026 All trademarks, copyrights, patents, and other rights of ownership to images
and text used on the RF Cafe website are hereby acknowledge My Hobby Website: My Daughter's Website: |
