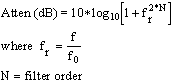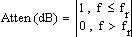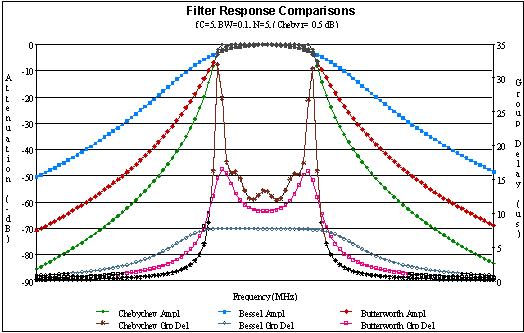
|
An infinite number of filter transfer functions exist. A handful are commonly
used as a starting point due to certain characteristics. The table following the
plots lists properties of the filter types shown below. Not given - due to complex
numerical methods required - are the Cauer (Elliptical) filters that exhibit
equiripple characteristic in both the passband and the stopband.
Click these links for full equations to calculate magnitude, phase, and group
delay of
Butterworth and
Chebyshev Type 1
lowpass, highpass, bandpass, and bandstop filters. They are implemented in my
RF Cafe Espresso Engineering Workbook™ (free download).
Phase information may be gleaned from the transfer functions by separating them
in to real and imaginary parts and then using the relationship:
Phase: θ = tan-1 (Im / Re)
Group delay is defined as the negative of the first derivative of the phase with
respect to frequency, or
Group Delay:
| Butterworth |
- Maximally flat near the center of the band.
- Smooth transition from passband to stopband.
- Moderate out-of-band rejection.
- Low group delay variation near center of band.
- Moderate group delay variation near band edges.
- Table of poles for N=1 to 10.
|
|
|
Chebyshev
Type 1
|
- Equiripple in passband.
- Abrupt transition from passband to stopband.
- High out-of-band rejection.
- Rippled group delay near center of band.
- Large group delay variation near band edges.
- Table of poles for N=1 to 10.
|
|
|
Bessel
|
- Rounded amplitude in passband.
- Gradual transition from passband to stopband.
- Low out-of-band rejection.
- Very flat group delay near center of band.
- Flat group delay variation near band edges[1].
- Table of poles for N=1 to 10.
|
Note: BN, PN, and boN must be placed
in a loop from 0 through
N.
|
|
Ideal
|
- Flat in the passband.
- Step function transition from passband to stopband.
- Infinite out-of-band rejection.
- Zero group delay everywhere.
|
(Heaviside step function)
|
| [1] Filters with a large BW will exhibit sloped group delay
across the band. This usually is not a problem since group delay deviation tends
to be specified for variation in some subsection of the band. |
| These equations are used to convert the lowpass prototype
filter equation into equations for highpass, bandpass, and bandstop filters. They
work for all three functions - Butterworth, Chebyshev, and Bessel. Simply substitute
the highpass, bandpass, or bandstop transformation of interest for the fr
term in the lowpass equation.
|
 Microwave Filters, Couplers
and Matching Network
by Robert J. Wenzel
This CD-ROM course contains approximately 12-hours of instruction on the fundamentals
of microwave filters, couplers and matching networks. Included is a thorough review
of the common types of filter responses and calculations, filter realization, and
various methods of filter design, including bandpass, network theory and Kuroda.
Subsequent sessions cover the fundamentals of directional couplers. A final session
describes distributed element matching networks and a matching network design example.
Related Pages on RF Cafe
-
Butterworth Filter Equations for Magnitude, Phase, and Group Delay
-
Chebyshev Filter Equations for Magnitude, Phase, and Group Delay
-
Butterworth Lowpass Filter Gain, Phase, and Group Delay Equations
-
Butterworth Highpass, Bandpass, & Bandstop Filter Gain, Phase, and Group Delay
Equations
- How to
Use Filter Equations in a Spreadsheet
- Filter Transfer Functions
- Filter Equivalent Noise
Bandwidth
- Filter Prototype Denormalization
- Bessel Filter Poles
- Bessel Filter
Prototype Element Values
- Butterworth Lowpass
Filter Poles
- Butterworth Filter
Prototype Element Values
- Chebyshev Lowpass Filter
Poles
- Chebyshev Filter
Prototype Element Values
- Monolithic
Ceramic Block Combline Bandpass Filters Design
-
Coupled Microstrip Filters: Simple Methodologies for Improved Characteristics
|
