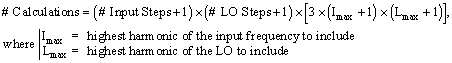|
Here is a reprint of an article I (Kirt Blattenberger) had published in Wireless
Design & Development magazine in 1995. Some of the references are a bit
dated, but the info is all still very useful. Waypoint Software is now RF Cafe,
and TxRx Designer is now Shareware by the name of
RF
Workbench.
With the advent of high speed personal computers, a very insightful graphical
method of determining inband mixer spurious products has been largely forgotten.
The Spur Web1 (a term I coined when I wrote the software) chart rapidly
identifies both inband and out-of-band spurs, affording a pictorial view of where
conversion system frequencies lie with respect to all spur products. To my knowledge,
this was the first use of the chart format in software of any kind. A comparison
will be presented between the Spur Web chart method and the common numerical method.
Contemporary efforts at identifying inband mixer spurious products consist of
employing a computer program, into which a range of frequencies is defined for the
input, output, and local oscillator (LO). A frequency step size or number of frequency
steps determines the resolution of the computation. If too few steps are specified,
then stepping past an inband spur is possible. If too many steps are specified,
then computation time becomes excessive and a long list of spur product frequencies
results. The number of computations for a given range of frequencies is governed
by Equation 1
Equation 1
Mixer spurious products exist due to nonlinear characteristics of diodes used
in mixer construction, mathematically resulting in the sum and difference of integer
value harmonics of input and LO frequencies. Theoretically the harmonics run to
infinity in a simple diode mixer; however, in practice harmonics greater than 9th
order often generate spur products that are below the noise floor and can be ignored.
Double balanced mixers tend to suppress odd order spur products to a greater degree
than even order products, while triple balanced mixers tend to suppress even order
spur products to a greater degree than odd order products. A spur product defined
by 3*I – 5*L is of the eighth order and is considered even (although both harmonics
are odd). In general, spur products take on the form given in Equation 2.
Equation 2
A 60 MHz computer can complete the necessary calculations in less than a second
for even large numbers of steps. Interpreting the data can take much longer, however.
To show how quickly the number of output frequencies can grow, Table 1 uses Equation
1 to predict the number of calculations for both fixed and variable input and LO
frequencies.
| # Input Steps |
# LO Steps |
I |
L |
# Spur Products |
| 0 |
0 |
6 |
6 |
147 |
| 50 |
0 |
6 |
6 |
7,497 |
| 0 |
10 |
6 |
6 |
1,617 |
| 50 |
10 |
6 |
6 |
82,467 |
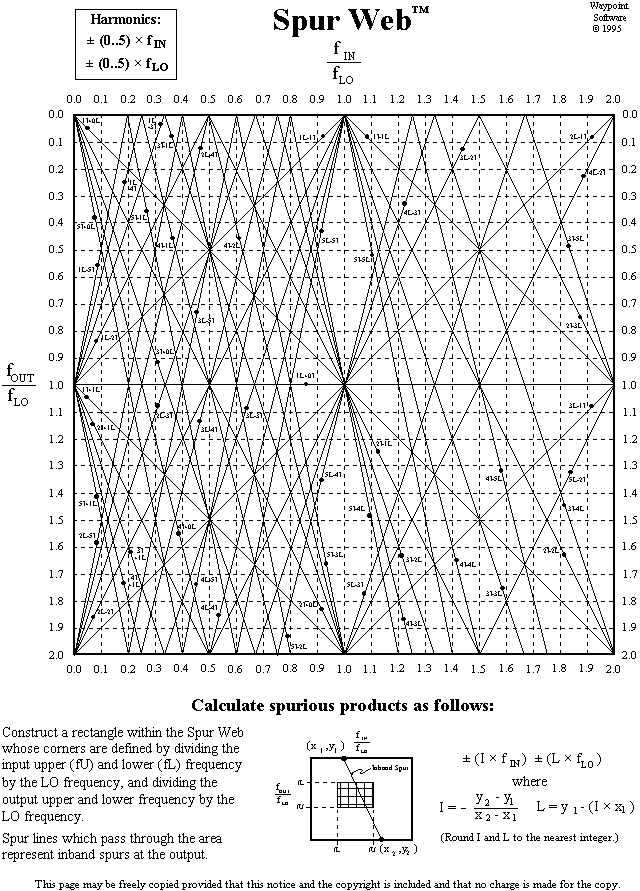
Table 1
Typically, the first range of frequencies tested is defined by input and output
filter passbands since the spurs generated within those bands cannot be filtered.
The next step would be to test a range of input frequencies below the lower input
band edge and a range of frequencies above the upper input band edge. Sufficient
steps in the input frequency must be used to guarantee that all possible spur products
are generated in the calculations. If a variable LO is used, then additional iterations
must be run to cover multiple values of LO frequency. Considerable amounts of time
can be spent sifting through all of the data generated by the aforementioned method.
Enter the Spur Web chart method of spurious mixer product detection. For the
record, I make no claim to have originated the method (my first encounter with the
chart was in an October, 1989, article in MSN magazine); I simply hope to resurrect
a seemingly lost art and to introduce a helpful standard chart. Figure 1 makes clear
why I dubbed the chart a Spur Web.
Choosing axis scales to represent ratios that are obtained by dividing the input
and output frequencies by the LO frequency allows straight lines to be drawn which
are defined by all spur products. The slope of a particular spur line is determined
by the harmonic of the input frequency (I) while the intercept of the spur line
with the vertical axis is determined by the harmonic of the LO frequency (L).
Similarly, the position within the Spur Web chart of a conversion system frequency
plan can be represented by scaling the input and output range of frequencies by
the LO frequency. Here, the input and output filter band edges constitute a good
choice for the frequency ranges. The calculated ratio values describe a rectangular
area within the Spur Web chart. All spur lines that pass through the rectangle are
representative of inband spurs at the output - again, those which cannot be filtered.
Figure 1
Both inband and out-of-band spur products are apparent using the Spur Web method.
If an intolerable spur product is looming just outside your filter band, then its
corresponding input and/or output frequency at any point can be inferred by multiplying
its x and/or y coordinate, respectively, by the LO frequency at the point of interest.
A major advantage is that the sample step size is infinitesimally small so stepping
over a spur product is impossible.
Evaluating a frequency conversion system with a variable LO is equally uninvolved.
Simply construct two rectangles within the Spur Web - one by scaling the input and
output frequencies using the lowest LO frequency (the larger rectangle) and one
using the highest LO frequency (the smaller rectangle). Connect the four corners
of the two rectangles with straight lines to create a wire frame object. Spur lines
that intersect the frame represent inband spurs at the output. Again, multiplying
any point on the chart by the particular LO frequency recovers the corresponding
input and output frequencies.
Referring back to Figure 1, the effects of using a high-side2
LO versus a low-side LO for either an upconversion or a downconversion becomes apparent
from a spurious product perspective. The associated spur products are vastly different
depending upon the position of the rectangle within the Spur Web chart. A particular
mixer model might provide superior suppression for a given set of spur products
in one region of the chart compared to another region, making a choice of high-side
LO versus low-side LO an obvious decision. Other factors, such as expense, might
outweigh the spur product considerations when selecting an LO.
As would be expected, the ±1*I ±1*L spur lines run diagonally from corner to
corner through each rectangular area, indicating that the fundamental conversion
frequencies define the rectangles. Although in the example all of the spur lines
are labeled, a simple set of equations defines each line and can be applied to identify
or create any spur line on the Spur Web chart. Using Equation 3 and Equation 4,
the values for the input harmonic and the LO harmonic can be calculated.
 Equation 3
|
Equation 4
|
Two unencumbered Spur Web charts are provided with this article. One chart includes
all input and LO harmonics from 0 through 5, with all spur lines labeled. The other
Spur Web chart includes input and LO harmonics from 0 through 9 when either of the
harmonics is equal to or greater than 6. Not all spur lines are labeled in the second
chart; however, Equation 3 and Equation 4 can be used to identify any unlabeled
spur line. Including all harmonics from 0 through 9 on a single chart would produce
an annoyingly cluttered chart.
Waypoint Software offers a unique frequency conversion CAE package named TxRx
Designer v3.0, that incorporates the Spur Web chart as a feature in the program.
A dynamic cursor readout provides corresponding input and output frequencies based
on the LO reference frequency. Per the foregoing discussion, the band edges of the
input and output filters are used to describe the rectangle boundaries within the
chart. Figure 2 illustrates how the high-side downconversion example of Figure 1
is presented by TxRx Designer v3.0. To demonstrate the full power of the method,
a variable LO is specified to cover a range of 130 to 150 (frequency units will
be omitted in the discussion).
All of the detected spur products for the 0 through 5th harmonics are listed
in the INBAND SPURS table to the left of the Spur Web chart. Note that the cursor
is positioned on the 2*LO – 3*RF spur line that passes through the upper left corner
of the backmost rectangle. With a reference LO frequency of 150.00, the indicated
IF Freq is 29.7520 (actually 30.0000, but limited by pixel resolution in this case)
while the indicated RF Freq is 90.0000. The CALCULATE SPUR LEVEL window is open
wherein the frequency of the spur product is verified. Additionally, the mixer spur
suppression for the spur product (derived from the mixer definition file) is displayed
along with the power level of the spur product at the system output (inclusive of
system gain and filter rejection).
Figure 2
Immediately apparent is that there are nearby spur lines that are not included
in the detected inband spur table. Simply moving the cursor to a point on a spur
line will reveal the input frequency that generated the spur product. The CALCULATE
SPUR LEVEL window can be used to determine the power level of the out-of-band spur
product at the system output, thereby ascertaining whether the filtering is sufficient
or whether a different mixer model will be required. Filter specifications can be
easily modified by clicking the mouse on a filter icon to open an edit window. Rerunning
the Spur Web calculation takes only a few seconds at most.
After a final configuration is achieved, simply print the screen for a permanent
record of the frequency conversion plan and the system components that are responsible
for it. For a record of the filter responses, switch to the graph screen and print
the system amplitude versus frequency.
Rather than spending valuable time running through multiple iterations of input,
output, and LO frequencies to analyze long lists of spur product frequencies, recommend
learning to use the Spur Web chart is highly recommended. The venerable Smith Chart3
revolutionized the solution of impedance computations in the pre-computer era and
has been carried over into the computer era via manifestations in many programs.
Hopefully, this reintroduction of the Spur Web chart and a demonstration of its
viability in a computer program will prompt inclusion of the Spur Web chart into
system analysis programs. A great service will hence be provided to designers at
a time when work overload is the rule rather than the exception.
Figure 3
Figure 4
- Spur Web™ is a trademark of Waypoint Software (now RF Cafe). I coined
the term (but not the chart format) when I wrote the TxRx Designer (RF Workbench)
software in the early 1990s. Spur Web™ is now widely used, but never attributed
to me.
- A high-side LO refers to an LO frequency higher than the input range of frequencies
for a downconversion, and an LO frequency higher than the output range of frequencies
for an upconversion. The converse is true for a low-side LO.
- Smith Chart™ is a registered trademark of Analog Instruments Company.
Posted March 2, 2007
|
