When plotted as voltage (V) as a function of phase (θ), a triangle wave looks similar to the figure to the right.
The waveform repeats every 2π radians (360°), and is
symmetrical about the voltage axis (when no DC offset is present). Voltage and current exhibiting cyclic behavior
is referred to as alternating; i.e., alternating current (AC). One full cycle is shown here. The basic equation
for a triangle wave is as follows:
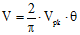 for 0 ≤ θ <
π/2
There are a number of ways in which the amplitude of a triangle wave is referenced, usually as peak voltage (Vpk
or Vp), peak-to-peak voltage (Vpp or Vp-p or Vpkpk or Vpk-pk),
average voltage (Vav or Vavg), and root-mean-square voltage (Vrms). Peak voltage
and peak-to-peak voltage are apparent by looking at the above plot. Root-mean-square and average voltage are not
so apparent.
 Also
see Sinewave Voltages and
Square Wave Voltages pages. Also
see Sinewave Voltages and
Square Wave Voltages pages.
Root-Mean-Square Voltage (Vrms) As the name implies, Vrms is calculated by
taking the square root of the mean average of the square of the voltage in an appropriately chosen interval. In
the case of symmetrical waveforms like the triangle wave, a quarter cycle faithfully represents all four quarter
cycles of the waveform. Therefore, it is acceptable to choose the first quarter cycle, which goes from 0 radians
(0°) through
π/2 radians (90°). Vrms is the value
indicated by the vast majority of AC voltmeters. It is the value that, when applied across a resistance, produces
that same amount of heat that a direct current (DC) voltage of the same magnitude would produce. For example, 1 V
applied across a 1 Ω resistor produces 1 W of heat. A 1 Vrms triangle wave applied across a 1 Ω
resistor also produces 1 W of heat. That 1 Vrms triangle wave has a peak voltage of √3 V (≈1.732 V),
and a peak-to-peak voltage of 2√3 V (≈3.464 V). Since finding a full derivation of the formulas for
root-mean-square (Vrms) voltage is difficult, it is done here for you.
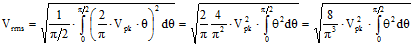
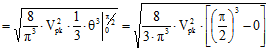
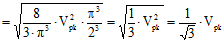
So,
 ≈ 0.577 Vpk ≈ 0.577 Vpk
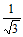 =
0.57735026918962576450914878050196 =
0.57735026918962576450914878050196
 =
1.7320508075688772935274463415059 =
1.7320508075688772935274463415059
Average Voltage (Vavg) As the name implies, Vavg is calculated
by taking the average of the voltage in an appropriately chosen interval. In the case of symmetrical waveforms
like the triangle wave, a quarter cycle faithfully represents all four quarter cycles of the waveform. Therefore,
it is acceptable to choose the first quarter cycle, which goes from 0 radians (0°) through
π/2 radians (90°). As with the Vrms formula,
a full derivation for the Vavg formula is given here as well.


So,
 ≈ 0.5 Vpk ≈ 0.5 Vpk
|



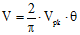 for 0 ≤ θ <
for 0 ≤ θ <
 Also
see
Also
see 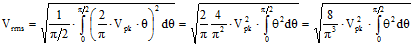
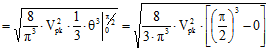
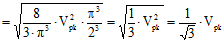
 ≈ 0.577 Vpk
≈ 0.577 Vpk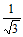 =
0.57735026918962576450914878050196
=
0.57735026918962576450914878050196 =
1.7320508075688772935274463415059
=
1.7320508075688772935274463415059

 ≈ 0.5 Vpk
≈ 0.5 Vpk

