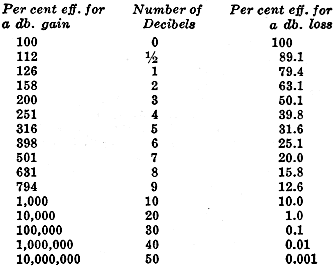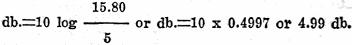Decibel Level vs. Decibel Gain
|
|
Arithmophobia (a real word) is likely the root cause of of decibelphobia (that one's made up), a condition that causes some otherwise rational people to curl in the fetal position in an attempt to avoid the topic. As with most subjects, the more often you engage in using a term, the more comfortable you become with it. Technicians and engineers who deal in voltage and power levels in terms of dividing quantities or transmitting them from one location to another would find conversation and writing without the use of decibels quite inconvenient. It is tempting to point out that using decibel units to express ratios or relative levels, thereby permitting use of simple addition and subtraction rather than multiplication and division, respectively, is no different than using logarithms to do the same with any number in general. However, logarithms are lost on most people as well. Historically, logarithms were so important in science and mathematics that large volumes were created to facilitate rapid multiplication and division of numbers. Just as it is unreasonable to go to a foreign country and expect the indigenous people to adapt their common language to accommodate your lack of knowledge*, if you expect to live in the realm of the RF and microwave world citizens, developing fluency in decibels is essential to a successful, productive existence. This article from a 1936 edition of Radio-Craft is as good a place to start as any. * Except for the case of the hoards crossing the U.S. southern border illegally with the expectation that we'll happily accommodate their native language and even provide all governmental communication in that language while berating protesting, legal citizens who are forced to pay for the policy. Oh, wait, that's what we do >:(
Related Pages: RF Cafe Decimal Tutorial
|
The Decibel Without Pain |
Using the Decibel | Decibel Tutorial:
dB and dBm vs. Gain and Milliwatts |
Versatile Voltage, Power, and Decibel Nomograms |
Decibel Level
vs. Decibel Gain |
A Decibel
Nomograph | The Decibel: AWG Wire
Size Rule of Thumb |
What is a Decibel? |
Understanding Decibels |
Decibels Without Logs |
The Useful Decibel | Decibels |
mW-to-dBm / dBm-to-mW Power Conversion |
NEETS: Decibel
Decibel Level vs. Decibel Gain - Do not miss this lucid explanation! S. L. Canterbury Amplifiers are rated according to the number of watts output they can handle without distortion. The output depends upon the size and design of the amplifier. This output tells what volume of sound will come from a system and the area that can be covered with the installation. The amplifier performs but one important function: to receive the voice of the speaker or music and raise the volume to a much higher level so that the sound energy may be heard by many people over a fairly large area. Basic Ratings Before the gain (amplification) of an amplifier can be measured it is necessary
to select some unit of measurement. As the output of the amplifier is rated in terms
of watts it would be logical to measure the input in terms of watts also. Now the
effect of sound energy on the ear is not a direct (arithmetic) function but varies
in an exponential way. Therefore, the gain of an amplifier is expressed in the same
way, by means of logarithms. The expression is given by the formula:
where db. represents the unit of transmission or amplification-the decibel; W0 is the power output; and Wi is the power input. The formula states that the "decibel gain" is equal to ten (10) times the logarithm of the efficiency of the amplifier. Efficiency is here used in connection with sound energy and does not mean the electrical efficiency which is usually very low. The above formula will hold at all times in rating amplifiers. Amplifiers can also be rated in terms of currents and impedances. Referring to Fig. 1, the formula is
If the resistance of the input impedance equals the load resistance, the 'last term becomes zero and the first term gives the decibel gain. In some designs, however, the second term may be considerable and must not be neglected in such cases. The gain may also be rated in terms of input and output voltages, provided the input and output reactances are equal to zero; that is, when both impedances are resistance only. The formula is:
Again the last term equals zero, if the input and output resistances are equal. The "Zero Level" Sound and noise levels are usually expressed in decibels and not in watts, therefore, a reference level of zero decibels must be set. For convenience, engineers have arbitrarily taken the output of a common-battery telephone transmitter (when spoken into with a loud voice) as zero level. This equals 0.01-watt or 10 milliwatts. The output of a standard transmitter, used by telephone engineers is also 10 milliwatts. Thus in telephone work zero level has been set at 10 milliwatts, but in radio work it will be noticed that the articles in the past have always mentioned the reference level and is not universally standard. The tendency among radio engineers is to refer the system to a zero level of 0.006-watt or 6 milliwatts and throughout this article all levels will be with respect to 6 milliwatts. It 's of very little importance whether the level is 10 or 6 milliwatts as long as one or the other is taken. as standard! By using 6 milliwatts as zero level, amplifiers may be rated at an energy level
of a certain. number of decibels. This is desirable because the ear responds to
sound in a logarithmic manner. This can be illustrated by the following example.
If an amplifier delivers 6 watts output it has a level of:
Now, if the output is doubled, the ear will notice an increase in volume but not twice as great as the 6 watts output because the ear will respond as the increase in decibels and not as the increase in watts output. Thus,
The ear did not detect the increased volume in a direct ratio, but as the logarithm of the ratio. Therefore, if this zero reference level were not used, the amplifier control set at 30 db. gain would not give any indication of the volume of the output unless the input were known. With the control marked in decibels above zero level, the 30 db. setting would indicate an output of 12 watts. A commercial amplifier rated at 26 watts out-put has an energy level, at full output, expressed in decibels equal to:
Now 'it is stated in the catalog that this amplifier has a gain of 96.4 db. Where do the extra 60 decibels come from? The answer to this question will become evident after the microphone output has been considered. Allowance for Mike "Level" Different types ·of microphones have different energy output levels, but most commercial-type carbon-button microphones give an energy level of -50 to -80 db. When the speaker (source of sound) is near the mike, a good average is the -60 db. level. The mike, therefore, lowers the energy level that it receives and it is the function of the amplifier to raise the voice level from -60 db. back to zero level and still higher in order to have appreciable output at the loudspeaker. After the sound has passed through the mike, it is at a very low level and has very little energy. The actual power impressed on the amplifier input, after passing through the mike, can be found as follows: -60 = 10 log R; where R is the ratio of mike output to mike input, and here it is assumed that zero level is impressed upon the mike. 40.0000 - 100 = 10 log R or 4.0000 - 10 = log R or
Thus the input of zero level to the mike is lowered to -60 db. in passing through the mike and the power that the amplifier begins with is very small. The entire gain is therefore 96.4 db. as the amplifier ends up with a 36.4 db. level. In amplification work it is desirable to know what level above zero the amplifier will raise the sound of the speaker's voice, and, therefore, the maximum reading on the control should be 36.4 db. and not 96.4 db. A high-gain amplifier when used with a very poor mike may give but little amplification. For example, suppose the mike had a loss of 76.4 db. This would leave a gain of 20 db. above zero. The output would be far below the rated 26 watts and would be equal to: 20 = 10 log R or 2.0000 = log R or
The energy required to operate the amplifier is 90 watts, while the output is but 26 watts. The efficiency is therefore
This may be expressed in decibels as would be done if used in connection with telephone work.
Table 1 - Decibel vs. percentage loss. The accompanying, Table I lists the efficiency for certain decibel gains or losses. The table's use can be demonstrated by means of the following examples. It is well to point out that the table may be used for any value of decibel gain. Suppose the efficiency at 15 db. gain is to be found. Fifteen decibels equal 10 db. plus 5 db. but the resulting efficiency is the product of the efficiencies at 10 db. and 5 db. A 15 db. gain gives an efficiency of 10 x 3.16 = 31.6 or 3,160 per cent. A Db. Gain in - Dollars! Let us now use this 15 db. gain in a problem. A man starts out with $2 and at the end of two weeks he has a 15 db. gain which is an efficiency of 3,160 per cent. Therefore, at the end of two weeks the man has $63.20. The man's son also has a decibel gain of 15 at the end of two weeks but he started with 50 cents. His efficiency is also 3,160 per cent but instead of having $63.20, like his father, the boy has only $15.80. Again it is seen that the db. gain is not as important as the db. level above a certain reference point. Suppose the reference point chosen by the two is $5.00, and this is zero db. level. The man at the end of 2 weeks, has a level of:
The boy has a db. level of:
level which shall be called a 5 db. level. With the level above, as the reference point, it is at once evident that the father has more money than his son. Both still have the same gain, however. In this case the man began with a -5 db. level and finished with 10 db., a gain of 15. The boy began with a -10 db. level and ended with a 5 db. level which is also a 15 db. gain.
Posted January 3, 2022 |
|


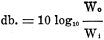

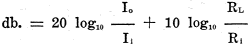
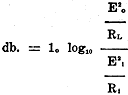
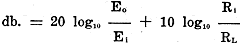
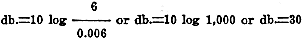 .
.
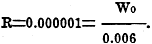 . Therefore W0
= 0.006-microwatt.
. Therefore W0
= 0.006-microwatt.  or the output W0
equals 0.6·watt. After all, the decibel gain is not so important. It is the decibel
level above zero that counts. It is well to point out here that there is a limit
to the over-all gain that an amplifier may have, as explained in Radio-Craft July
1935, page 10.
or the output W0
equals 0.6·watt. After all, the decibel gain is not so important. It is the decibel
level above zero that counts. It is well to point out here that there is a limit
to the over-all gain that an amplifier may have, as explained in Radio-Craft July
1935, page 10. 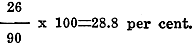
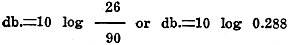 or
or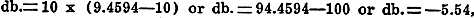 which represents a loss.
which represents a loss.