|
August 1965 Electronics World
 Table
of Contents
Table
of Contents
Wax nostalgic about and learn from the history of early electronics. See articles
from
Electronics World, published May 1959
- December 1971. All copyrights hereby acknowledged.
|
Not so very long ago the availability
and usage of lasers
was restricted to laboratory and military use, but today they are ubiquitous in
our world. CD, DVD, and Blu-ray players are found in nearly every home and office.
Laser pointers (including the green ones being illegally
targeted on aircraft), laser distance measuring devices, laser leveling and
alignment tools, laser light shows, laser cutting, even laser weapons can be found
in many other venues, and at relatively low costs (except
the weapons). Half a century ago, most lasers were fabricated from rare earth
elements whose output powers were measured in a few milliwatts at most. The cost
of even a low power laboratory experimental device was thousands of dollars. I can
remember seeing something like a 0.5 mW helium-neon laser for hobbyists offered
by Edmund Scientific back in the 1970s for about $200, and much more for a laboratory
quality laser. Power supplies were hundreds of volts. Typical laser pointers put
out around 5 to 10 mW and are made from tiny chips of semiconductors powered
by pen cells or button cells. This Electronics World magazine article is a fairly extensive report on the state
of laser science in 1965.
Lasers
 By Warren Groner Sr. Engineer, Electro-Optics
Group Sperry Gyroscope Co. By Warren Groner Sr. Engineer, Electro-Optics
Group Sperry Gyroscope Co.
An authoritative explanation of the operation of solid and gaseous lasers.
The significance of such effects as coherence, population inversion, photon amplification,
and stimulated emission is made clear.
Editor's Note: This is the first in a group of three articles on lasers. Our
objective is to provide the reader with a clear and accurate understanding of laser
operation. Future issues will feature articles covering the modulation and demodulation
of a laser beam, the injection laser, applications, and laser measurements.
The first experimental production of electromagnetic waves by Hertz in 1888 ushered
in the age of radio communication. The reader is surely familiar with the growth
and importance of the communications industry. The milestones which mark its progress
are numbered in consecutive orders of ascending frequency.
The reason for expanding the communications spectrum toward the higher rather
than the lower end is that the rate of information (e.g., video signals) which can
be transmitted is directly proportional to the center frequency of the carrier wave.
In addition, motivation has been furnished for the expansion of the electromagnetic
spectrum by the greater atmospheric penetration of shorter wave-lengths, by the
increased directionality of transmitted power at higher frequency, and the needs
of various interested parties.
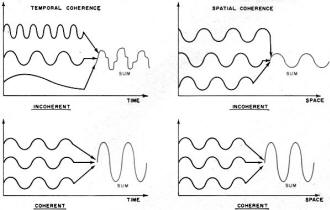
Fig. 1 - The effects of temporal (in time) and spatial (in
space) coherence on three waves.
A technician, eyes protected by dark goggles from the white-hot
glare of light, monitors growth of a laser crystal boule. Painstaking eight-hour
process starts with a crystal "seed" dipped into a crucible filled with molten raw
laser crystal materials. Fixed to a slowly rotating rod, the seed is pulled up a
half inch an hour. The molten metal adheres to the seed and cools and hardens as
it is drawn from the crucible. The crystal looks like a small icicle before it is
cut, machined, and then polished into a usable, commercial laser rod.
It is curious that ordinary light, recognized early in the game as electromagnetic
waves of extremely high frequency ( ≈1015 cps), was never exploited
for communications purposes. To understand the reason for this neglect and appreciate
the importance of the laser, it is necessary to consider what is required of a transmitter
in a communications link. An effective transmitter is a generator of electromagnetic
waves which radiates a significant amount of coherent power in a narrow band of
frequencies, including the particular one of interest. But why is coherence desirable?
Need for Coherence
The need for coherence in an efficient generator is sometimes overlooked by
the radio or microwave engineer. For example, the tacit assumption made when he
designs or builds an antenna for a receiving system is that increasing the area
over which the signal power is collected will increase the signal-to-noise ratio
at the detector. However, this is true only if the phase of the incoming signal
is constant or varies in a predictable manner over all points of the antenna. If
the phase of the incoming signal changes in a random way from point to point over
the antenna, then the detector can sum only the absolute value of the incoming power.
The sum of phase angles will be zero, in general, and all modulation will be lost.
This correlation of phase in the signal is just what is meant by coherence. An instantaneous
correlation of phase from point to point in space is called "spatial coherence"
and a consistent correlation in phase at two neighboring points over a length of
time is called "temporal coherence" (see Fig. 1).
The generators of radio, television, and radar signals exhibit both temporal
and spatial coherence in the emitted signal. Until the advent of the laser, however,
no sources of signal power operating in what is known as the optical spectrum were
coherent in any but a statistical sense. This fact, more than any other, has precluded
the highly desirable use of these frequencies for communications other than simple
"on-off" switching.
The reason for the lack of coherence in optical sources other than the laser
is related to the lack of correlation among the motions of the electrons, each electron
behaving as a tiny oscillator which emits light. For familiar light sources, such
as tungsten filaments and gas-discharge tubes, electrical energy is supplied to
create conditions favorable to the emission of light, e.g., by heating the filament
or exciting the atoms in the gas. The actual emission process, however, is uncontrolled.
Each oscillator radiates independently of its neighbors. Thus the emitted light,
which is just the sum of all the individual radiations, lacks both spatial and temporal
coherence. The idea of maintaining a constant phase relation over the oscillators
by stimulating their emission with a wave of the frequency to be radiated was first
proposed by C.H. Townes in 1958. Two years later, utilizing stimulated emission,
Theodore Maiman achieved pulses of coherent optical radiation from a single ruby
crystal.
Since that time the development of the laser, an acronym for Light Amplification
by Stimulated Emission of Radiation, has proceeded at a phenomenal pace. The intensity,
monochromaticity, and polarization of laser radiation has created potential applications
in medicine, industry, and scientific measurement, in addition to the obvious application
to communications. In conjunction with this spectacular growth, recognition of the
importance of the laser, or optical maser as it is sometimes called, has become
widespread. A billion-dollar laser market by 1970 has been predicted, and in 1964
Professor Townes was a co-recipient of the Nobel Prize for his pioneering work in
this field.
The importance of the laser to the engineer and technician cannot be sufficiently
stressed. Before learning the fundamentals of laser operation, some preparation
is required. The laser is often referred to as a "quantum-electronic" device thus
necessitating the introduction of some important concepts of modem or quantum physics.
Some Ideas of Modern Physics
In 1900 Max Planck formulated an accurate description of the spectrum radiated
from a black body. (A black body is a perfect radiator or absorber of energy.) Planck
offered the revolutionary hypothesis that the energies of the electron oscillators
responsible for the radiation are quantized, that is, restricted in certain integral
multiples of a constant which now bears his name.

Fig. 2 - The Bohr model of the hydrogen atom showing electron
jumping from one energy level to another and emitting radiation.
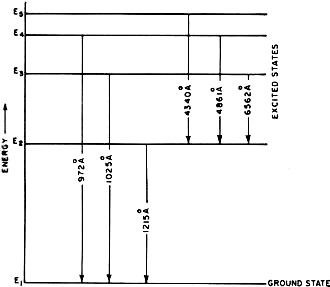
Fig. 3 - Energy-level diagram for the Bohr model of hydrogen
atom. When electrons make transitions from a higher energy level to a lower energy
level, then radiation having a certain specific wavelength (in angstroms) and frequency
is produced.
Although not too well understood at the time, Planck's "quantum" hypothesis was
successfully employed by Albert Einstein in explaining, among other phenomena, the
photo-electric effect. In explaining the photoelectric effect, Einstein extended
the "quantum" concept to the radiation itself, by assuming that light interacts
with electrons in a metal as if the light were itself composed of discrete bundles
of energy whose energy E is given by E = hf where h = Planck's constant and f =
frequency of radiation. Consequently, a light beam can be thought of as a stream
of massless particles called photons which travel at the speed of light. Each particle
contains an energy of hf joules.
In 1913, Niels Bohr gave the quantum theory a big boost by proposing a quantized
model for the hydrogen atom. In Bohr's model the hydrogen atom is pictured as a
small, positively charged nucleus orbited by an electron. Bohr postulated that the
rotational energy of the orbiting electron can have only certain discrete values.
These values define a set of stable electron orbits, that is, while an electron
is rotating in a stable orbit it does not emit radiation. A region which separates
allowed energy levels is called an energy gap. The electron could change energy
only in a jump in which it either absorbed or emitted a photon. Thus, the conservation
of energy for an electron jump may be written as Em - En = hfm,n
where Em and En are two allowed energy states for the orbiting
electron, and fm,n is the frequency of the emitted radiation. Fig. 2
shows this for energy levels corresponding to m = 2 and n = 1.
Using Bohr's model, one could calculate the frequencies of the emitted radiation
and it was found that these frequencies agreed almost perfectly with the observed
characteristic spectrum of hydrogen.
In the years following the introduction of Bohr's model, quantum theory grew
in significance and power. Many changes were made and even a brief sketch of this
development would carry us too far afield for the task at hand. However, some of
the features of the Bohr atom provide a useful introduction to the important concepts
necessary to the description of laser operation.
A graphical picture of the Bohr model in terms of energy is given in Fig. 3,
where energy is plotted on the vertical scale. The horizontal lines are the allowed
energy levels and the vertical connecting lines represent examples of electron jumps
or "transitions" with the wavelength of the emitted radiation given along the transition
lines in angstroms (1 angstrom = 10-10 meter). Energy
level E1 denotes the lowest energy level or ground state for the atom.
The other levels (E2, E3 .... ) represent excited states.
Such a representation is called an energy-level diagram.
The usefulness of these diagrams in atomic physics may be appreciated when one
realizes that the energy-level diagram for a given atom is peculiar to that type
of atom. The energy-level diagram for an atom is to the atomic physicist what the
schematic is to the electronics technician because such a diagram exhibits important
information about atomic behavior.
Lifetime & Population of Levels
One feature of an atom's behavior not included in an energy diagram is the lifetime
and population of levels. That is, if the atom at some given time is in an excited
state (its electrons are at any level except the ground state), will it remain there
for all time if undisturbed, or will it spontaneously jump to some other level and
emit radiation? The answer to this question is that there is always a tendency for
an atom to return to its lowest energy or ground state. Consequently it will spontaneously
make transitions downward until the ground state is reached. For a gas of unexcited
atoms almost all atoms will be in the ground state.
The situation, however, is complicated by the fact that the average time an atom
remains in a state before decaying to some lower level depends on what state it
is in to begin with. Therefore, in order to complete the picture, a set of numbers
must be made available which represents the mean lifetimes of the electron in all
its possible states before it decays spontaneously. In general, these lifetimes
are quite short, <10-8 second. However, there exist levels for which
the lifetime is considerably longer and these are known as metastable states. It
also must be remembered that each of the spontaneous transitions must conserve energy
and therefore is accompanied by the emission of a photon. Photons emitted by spontaneous
transitions are called spontaneous emissions. Because one atom does not know what
another atom is emitting, there is lack of interaction among atoms, and the resulting
emission that is produced is incoherent.
Stimulated Emission
Recalling what was said earlier about ordinary light sources, it would appear
that these sources rely on spontaneous emissions for their output. Spontaneous transitions
are not the only means by which a particular atom may return to its ground state.
Consider the hypothetical case of a coherent light or photon beam traversing
atoms of a gas.

Experimental laser radar resembles a battery of rocket launchers
as it is set up for a test. In operation, the laser beam flashes from the transmitting
telescope (right) and bounces back off a distant target into the receiving telescope
(left). Two smaller telescopes are used for alignment and photography.
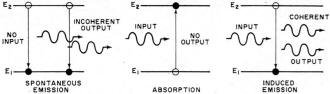
Fig. - Atomic transitions producing emission and absorption.
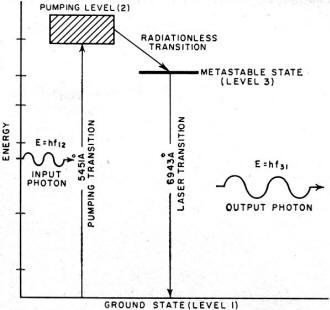
Fig. 5 - The three levels of the chromium ion in a ruby
rod which is involved in pumping and in laser action.

Fig. 6 - (A) Output of ruby laser. Time scale is 0.1 millisec./div.
The envelope is the pump-lamp flash. (B) Expanded portion of the trace with time
scale of 1 μsec./div. Incidentally, in the scope traces shown time proceeds from
right to left rather than left to right.
When the frequency of such a source coincides with one of the frequencies of
spontaneous emission, atoms are induced to make transitions between two particular
energy levels whose difference is ΔE and satisfy the relation ΔE = hf.
An important result is that transitions from the upper to lower energy states are
induced in addition to those in the opposite direction. In fact, the probability
that the induced transition will be in one direction rather than the other depends
only on which level the majority of atoms find themselves. When the transition is
from a lower to an upper energy level (accompanied by the loss of one photon from
the beam), it is called absorption, and when the transition is from upper to lower
energy levels a photon is emitted and it is called induced or stimulated emission.
Note that in this case the emission was induced by the presence of an energy source.
If equal numbers of atoms are in each of two levels the beam intensity will remain
constant in traversing the gas. For more atoms in the upper than in the lower state
the beam will see a net gain of photons or will be amplified by stimulated emissions
in traversing the gas. Because photon emissions will be induced by interaction with
the photons in the beam, which were assumed coherent, they will all be in phase,
and the amplified beam will be coherent (see Fig. 4). In this way a single
spontaneous emission may be amplified into an intense coherent beam. The remaining
problem to solve is to obtain the higher concentration of atoms in the upper energy
level necessary for amplification. This is known as population inversion, and this
particular topic will be treated for the particular case of ruby in the next section.
The Ruby Laser
Obtaining population inversion involves the addition of energy to the gas. The
process of populating an upper energy level at the expense of a lower one is called
pumping. One possible method of pumping between two levels whose difference in energy
is ΔE is by supplying electromagnetic energy of the frequency satisfying the
relation hf = ΔE and thus raising the energy by absorption. This method is
efficient only at the start, when the population of the lower level exceeds that
of the upper. As equal population is obtained the number of upward transitions becomes
equal to the number of downward transitions irrespective of the pumping energy.
Thus, to obtain inversion, a more sophisticated technique is necessary, involving
at least one intermediate energy level upon which the pumped atoms may be stored.
A simple example of the three-level system is in the chromium ions present in
chromium-doped aluminum oxide, more familiarly known as ruby. Before continuing,
it must be observed that since the essential property of a gas is that the constituents
do not interact with one another, a lightly doped (<<1%) crystal is essentially
a gas of dopant atoms in a rather special container. However, their energy levels
are somewhat modified by the presence of the host material. A simplified energy
level diagram of the chromium ion in a ruby crystal is shown in Fig. 5. The
intermediate level (3) is metastable with a lifetime of approximately 10-3
second. The operation is as follows:
A pumping light of frequency ƒ12 causes transition between levels
(1) and (2). The atoms in the excited (2) state may return to the ground state spontaneously
either directly or by first stopping at the metastable state. Because the lifetime
of the metastable state is 100,000 times longer than that of state (2), the atoms
which fall there may be considered almost stationary. The rate at which atoms find
themselves in state (3) is proportional to the rate at which they arrive in (2)
which, in turn, is proportional to the pumping power and independent of the population.
Thus, if sufficient pumping power is supplied, the population of the (3) state will
grow at the expense of the (1) state without the limitation imposed on the two-level
system, and population inversion is obtained.
As long as the population is inverted, the ruby can be an amplifier for radiation
of frequency ƒ31 and, as with any amplifier, adding a positive feedback
loop can cause sustained oscillation. In this case what is meant by positive feedback
is the return of some of the output light (ƒ31 radiation) into the
ruby. This may easily be accomplished with mirrors. In fact, by making use of the
geometry of the mirrors so that the feedback is directional, a resonant cavity is
formed. The amplified radiation, referred to as photon amplification, will build
up in a standing-wave pattern familiar in microwave technology.
The resonant cavity is formed from the crystal itself by carefully grinding and
polishing the ruby and silvering its ends. Because of the shortness of optical wavelengths,
an essential difference exists between our crystal cavity and the more familiar
microwave cavity. Calculating the wavelength from the energy-level diagram, the
wavelength corresponding to ƒ31 radiation is found to be 6943Å
in vacuum. Thus a ruby ground to form a cavity 7.3 cm. long (a typical size), has
100,000 nodes in the standing wave and will be resonant for every frequency that
satisfies the standing-wave condition: (n/2)λ = L where λ
is the wavelength and n an integer. For example, taking n as 105, the
difference between resonant wavelengths Δλ is given by: (Δλ/λ) = (Δƒ/ƒ) =
1/n = 10-5. The cavity is resonant for a large number of frequencies
right around ƒ31 instead of being resonant for only one particular
frequency as in the microwave case.
Practical Considerations
Before turning to a description of operation of the helium-neon gas laser, it
is worth mentioning some practical considerations which arise in carrying out the
scheme just described. First, the pumping power required to obtain population inversion
for a reasonable size crystal is considerable, and may be accomplished only in brief
bursts of light from a flash lamp. The operating time of the ruby laser is therefore
limited to a couple of milliseconds. Second, while the ruby is lasing, the metastable
state is being depopulated by stimulated emission, and quickly (in 10-6
second) outruns the pump, causing lasing action to stop until the pump can again
create a population inversion. Hence, the output of a ruby laser consists, typically,
of a series of irregularly spaced spikes about 10-6 second in duration
in an envelope defined by the pump lamp duration. Fig. 6 shows an oscilloscope
trace of the output of a photo detector receiving light energy from a ruby laser.
Finally, we may consider the over-all efficiency of the ruby laser by forming
a percentage from the ratio of total output of laser light energy to the electrical
energy supplied to the pump. This efficiency is typically less than 1% with most
of the lost energy heating the ruby. This makes cooling the crystal an important
practical consideration.
The Gaseous Laser

Fig. 7 - Operation of four-level system as in gaseous laser.
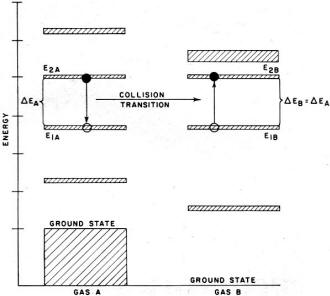
Fig. 8 - Example of resonant transfer by collision of gas
atoms.
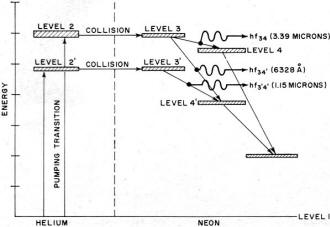
Fig. 9 - Energy levels of helium and neon during laser action.
To understand the operation of the helium-neon gas laser, a different means of
obtaining population inversion as well as of pumping must be considered. The modification
of the energy-level scheme is shown in Fig. 7. Note that a fourth or terminal
level has been added above the ground state. The population inversion is now obtained
between the (3) and (4) levels. The advantage of the four-level scheme is that the
initial population of the terminal level is negligible compared to the ground state
and therefore inversion is more easily obtained (i.e., less atoms in the (3) state
are necessary for its population to exceed that of the (4) state than that of the
ground level) . This reduces the pumping power required and opens up the possibility
of pumping by a different method, called electron-collision pumping.
In quantum theory a striking analogy is found for an electron beam traversing
atoms of gas and that of a photon beam. Only when the kinetic energy of the electrons
coincides with the differences in energy between any two levels are atoms induced
by collisions with the electrons to make transitions between these levels. As in
the electromagnetic case, the most probable direction of the transition depends
only on the relative populations of the states. Hence, as an alternative, we may
consider pumping atoms of gas with accelerated electrons in a discharge tube instead
of by a light beam. These may be the result of a glow discharge when r.f. energy
is applied to the discharge tube. The obvious advantage of this method is we can
maintain this energy constant over extended periods of time and obtain a continuous
laser output. This presupposes the availability of sufficient pump energy for inversion.
The first successful operation of a laser by collision pumping required the presence
of two gases, such as helium and neon, in the discharge tube to realize the proper
energy scheme. A slight digression is necessary to consider the transfer of energy
between atoms of different gases. A sort of resonance phenomenon is encountered
where energy transfer proceeds only when an energy gap is shared. That is, an atom
of one type of gas (A) in a given energy level (2A) may transfer its energy to
an atom of another type (B) in a stage (1B) via a collision if, and only if, there
exist energy levels 1A and 2B such that E2A - E1A = E1B - E2B
(see Fig. 8). As before, the probability of the transition direction is determined
by the population of the levels.
In this gas laser, the higher and lower energy levels are in different gases,
and their population may be modified by changing the relative concentration of the
different gases in the discharge tube. This additional control was fundamental in
achieving the first observed laser action in a gaseous mixture of helium and neon.
Fig. 9 shows the pertinent sections of the energy-level diagrams for helium
and neon with the transitions indicated. Note that when the (3) level is well populated
by pumping energy, there is amplification for two different frequencies, ƒ34
and ƒ34' Note also that the alternate route 1, 2', 3', 4' should
result in amplification at the frequency ƒ3'4'. Lasing action has
been observed at all of these frequencies in helium-neon mixtures. Selection of
oscillation between these frequencies is accomplished by using feedback mirrors
with reflectivities at the different frequencies.
It must be pointed out that the above discussion by no means covers all known
lasers. In fact, the list of laser materials grows on an almost weekly basis. Laser
action has been observed in other solids doped with small quantities of rare earth
ions, almost all the noble gases, and even in some special liquids. In addition,
the observation of coherent light generated by injection currents in semiconductor
diodes such as gallium arsenide and gallium phosphide has added another important
class of laser (called injection lasers) to this fast-growing field.
It is interesting to compare in a general way the helium-neon laser to the ruby
crystal laser. In the first place, the atoms in a gaseous discharge tube are more
widely spaced than the dopant atoms of even a slightly doped solid. A longer path
length in the discharge tube is usually necessary to obtain sufficient optical gain
for lasing. The helium-neon laser resonant cavity is, therefore, generally larger
than that of a ruby laser. However, the over-all efficiency of the helium-neon laser
(total laser output power/pumping power) is considerably higher than that of ruby.
Consequently, power supplies for ruby lasers are most often larger than those for
the helium-neon type.
The most striking difference between these devices is in their outputs. Whereas
the ruby laser output is typified by irregular spiking, the helium-neon laser is
capable of a continuous wave of extremely narrow bandwidth. This great disparity
in emissions has divided the two types of lasers into their respective fields of
application. Microsurgery, microwelding, micromachining, and pulsed-type communications
systems require high instantaneous powers for short durations and consequently have
adopted the ruby laser. On the other hand, continuous communications requiring
sophisticated demodulation techniques such as heterodyning, as well as the practical
usage of light interferometry, find the gaseous type of lasers well suited for this
particular application.
Posted October 11, 2022
(updated from original post
on 6/30/2015)
|





















