|
February 1950 Electronics
 [Table of Contents] [Table of Contents]
Wax nostalgic about and learn from the history of early electronics.
See articles from Electronics,
published 1930 - 1988. All copyrights hereby acknowledged.
|
If
Phillip H. Smith, an
engineer notable for his varied and complex qualities, was around today, he
would undoubtedly be known as "Mr. Impedance," although his humble character
would resist the admittance of stardom into his biography. Anyone as adept at
designing impedance matches, calculating phase changes along a transmission
line, and determining capacitances and inductances, surely has, during routine
tasks of his workday, calculated optimal ratios of inner and outer conductor
diameters which result in minimum antiresonant impedance (∞ Ω), maximum antiresonant impedance
(32.9 Ω),
minimum attenuation, maximum breakdown voltage (59.93 Ω), minimum
temperature rise (36.38 Ω), maximum power carrying (29.94 Ω), and, duh, minimum
resistance (0 Ω). Graphics, plots, and even a nomograph are included.
Optimum Coax Diameters

Fig. 1 - Quick picture of optimum coaxial conductor diameter
ratios.

Fig. 2 - Characteristic impedance in ohms of gas-filled coaxial
line for various conductor diameter ratios.
By Phillip H. Smith,
Technical Staff Bell Telephone Laboratories, Inc. Whippany, N. J.
Equations and charts give optimum ratios of inner and outer conductor diameters
for each of ten different transmission line properties. Comparison of curves speeds
choice of best compromise ratio for a particular application. Expanded scales give
Zo for any ratio.
If the inner diameter D of the outer conductor of a coaxial transmission line
is held constant and the diameter d of the inner conductor is varied, optimum conductor
diameter ratios for different transmission line properties will range from one to
infinity as indicated in Fig. 1. It is frequently advantageous to employ a coaxial
line having a conductor diameter ratio which results in a compromise between several
desirable line properties. A single compromise ratio is also desirable for certain
fields of use because it simplifies manufacturing and merchandising problems. These
considerations have led to standardization, in effect, of a single coaxial conductor
diameter ratio for high - frequency and microwave applications1. This
ratio (2.3) results in a nominal characteristic impedance of about 50 ohms. For
many specific coaxial line applications, however, the design engineer may find it
desirable to employ a conductor diameter ratio which will give more nearly optimum
results.
The derivation of the optimum ratios is briefly described and optimum values
are indicated to one part in ten thousand. In all cases the medium between conductors
is assumed to be a gas with a dielectric constant approaching unity, and any effect
of inner conductor supports upon the optimum conductor diameter ratio for a given
property is neglected.
The relationship between conductor diameter ratio and characteristic impedance,
as plotted on the expanded scales of Fig. 2, is based on the familiar equation
Z0 = 138 log10(D/d)
(1)
Attenuation and Attenuators
For a given frequency and conducting material the total high-frequency resistance
R of a coaxial transmission line is proportional to the inverse sum of the diameters
of the individual conductors:

This equation shows that minimum resistance of a line of given outer conductor
diameter D occurs when ratio D/d approaches unity. Minimum resistance does not,
however, accompany mini- mum attenuation. As the conductor diameter ratio approaches
unity the resistance approaches 0.435 times the resistance of a line having minimum
attenuation, as seen from Fig. 3.
Minimum attenuation, commonly referred to as loss in a coaxial transmission line,
occurs when ratio D/d is 3.592. This ratio corresponds to a characteristic impedance
of 76.64 ohms.
As the conductor diameter ratio drops below the minimum-attenuation ratio of
3.592 the line resistance continues to decrease but the current required to transmit
the same power through the line rises. For ratios below 3.592 the PR losses mount
at a rate that is faster than the rate at which the resistance decreases.
The attenuation constant of the line and not the resistance alone determines
the overall attenuation. The attenuation constant a of a high-frequency transmission
line is
α
= R/2 Z0
(3)
Substituting Z0 from Eq. 1,
α
= R / [276 log10 (D/d)]
(4)
But from Eq. 2 R is proportional to [(1/d) -I- (1/D)]. Substituting this for
R in Eq. 4, we obtain
α
= K * [(1/d) + (1/D)/ log10 (D/d)] (5)
where K is a proportionality factor. The conductor diameter ratio corresponding
to minimum attenuation is obtained by minimizing a with respect to D/d.
The increase in attenuation2 as a result of departing from the optimum
ratio of 3.592 is obtained from Eq. 5 when the proportionality factor K equals log10[3.592/(3.592
+ 1)] or 0.121. Figure 3 shows this graphically.
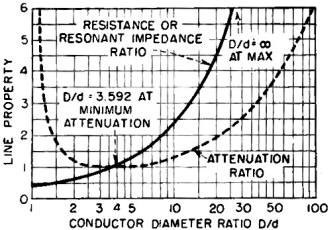
Fig. 3 - Solid-line curve gives effect of D/d on ratio of resistance
or resonant impedance of line to that of line having minimum attenuation. Dashed
-line curve gives effect of D/d on ratio of attenuation of line to that of line
having mini- mum attenuation.
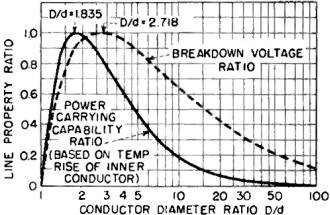
Fig. 4 - Solid-line curve gives effect of D/d on ratio of power
carrying capability of line to that of line having maximum capability. Dashed -line
curve gives effect of D/d on ratio of breakdown voltage to that of line having maximum
resistance to breakdown
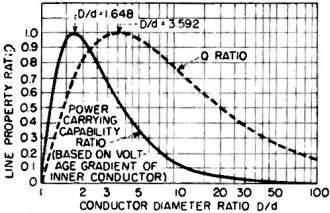
Fig. 5 - Solid-line curve gives effect of D/d on ratio of power-carrying
capability of line (based on voltage gradient of inner conductor) to that of line
having maximum capability. Dashed-line curve gives effect of D/d on ratio of Q of
line to that of line having minimum attenuation.
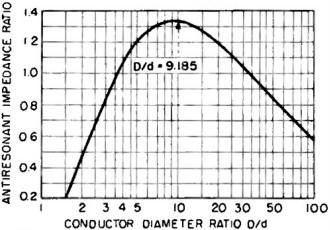
Fig. 6 - Effect of D on ratio of anti-resonant impedance of line
to that of line having minimum attenuation.
Heat, Voltage and Power
The optimum conductor diameter ratio of a coaxial line based on temperature rise
of the inner conductor may, with certain simplifying assumptions, be computed by
multiplying the attenuation constant, as expressed by Eq. 5, by the area ratio of
outer to inner conductor per unit length (which equals the ratio of diameters) and
then minimizing with respect to D/d. An optimum ratio of 1.835 is thus obtained,
which corresponds to a characteristic impedance of 36.38 ohms.
The calculated3 penalty in decreased power-carrying capability based
on a constant temperature rise of the inner conductor, for departing from this optimum
ratio, is shown on Fig. 4. The penalty in increased temperature rise of the inner
conductor for departing from the ratio 1.835 will vary for different conditions
of inner and outer conductor emissivity and thermal properties of the surrounding
media, and therefore can be evaluated quantitatively only in specific cases3.
A coaxial transmission line will withstand maximum applied voltage between conductors
when their diameter ratio is 2.718, which corresponds to a characteristic impedance
of 59.93 ohms. This is determined by minimizing the formula for the voltage gradient
at the surface of the inner conductor4, where breakdown first occurs,
with respect to D/d. The gradient g in volts per cm at the surface of the inner
conductor is
g = 2 * E / (d log10(D/d)]
(6)
where E is the applied voltage and e is the Napierian base (2.718). The reciprocal
of g gives a quantity which is proportional to the ratio of the breakdown voltage
of a line to that of a line having maximum resistance to breakdown. This is plotted
on Fig. 4 as a function of the conductor diameter ratio.
Maximum power-carrying capability of a concentric transmission line occurs when
the conductor diameter ratio equals √e or 1.648, which corresponds to a characteristic
impedance of 29.94 ohms5. This assumes that the frequency is within a
range (usually below about 50 mc) where voltage breakdown rather than overheating
of the inner conductor governs the maximum power rating of the line. This ratio
is also optimum from the power -carrying standpoint at higher frequencies under
most conditions of pulsed operation where the average power is small as compared
to the peak power.
In order to calculate the maximum power-carrying capability ratio, based on a
limiting voltage gradient on the inner conductor, we note first that the applied
voltage across a transmission line terminated in its characteristic impedance is
a function of the characteristic impedance and the power P in the line:
E = √(PZ0)
(7)
But the characteristic impedance as given by Eq. 1 may also be expressed as
Z0 = 60 log10 (D/d)
(8)
Substituting into Eq. 7,
E = √(60 * P) * √[log10 (D/d)]
(9)
The gradient at the surface of the inner conductor for a given applied voltage
is given by Eq. 6. Substituting the above equivalent for E into Eq. 6 we obtain
the following expression for the gradient at the surface of the inner conductor
for a given power
g = 2 √(60 * P) / 2 √[log10 (D/d)] (10)
The conductor diameter ratio which permits the transmission of a given power
with minimum voltage gradient, and hence maximum power transmission when voltage
gradient is the limiting factor, is obtained by minimizing g, as given in Eq. 10,
with respect to D/d. We then obtain (D/d) = √e = 1.648. The square root of the reciprocal
of the gradient as expressed in Eq. 10 gives a quantity which is proportional to
the ratio of the power -carrying capability of the line to that of a line having
a maximum capability, based on minimum voltage gradient on the surface of the inner
conductor. This is plotted as a function of the conductor diameter ratio in Fig.
5.
Antiresonant Impedance
The maximum antiresonant impedance of coaxial transmission line sections is obtained
when the conductor diameter ratio is 9.185, which corresponds to a characteristic
impedance of 132.90 ohms6. The antiresonant impedance of a transmission
line section is, in general
ZAR = Z0/α
(11)
where α
is the attenuation constant of the line. Substituting the value for Z0
given by Eq. 1,
ZAR = log10 (D/d) /
α
(12)
a Combining this with Eq. 5 then gives
ZAR = log210 (D/d) / [(D/d) + 1]
(13)
The conductor diameter ratio which provides a maximum anti-resonant impedance
for a line section is obtained by maximizing ZAR with respect to D/d.
The absolute value of the anti-resonant impedance for a transmission line of
optimum conductor diameter ratio (9.185) may be computed from
ZAR = 3,428.82/R
(14)
where R is the total resistance of the line section.
Resonant Impedance
Minimum resonant impedance of a coaxial line section is obtained when the conductor
diameter ratio approaches the limiting value of unity. As the ratio approaches this
limiting value the characteristic impedance approaches zero.
The resonant impedance of a line section is, in general,
ZR =
α Z0
(15)
Substituting the value for Z. given by Eq. 1
ZR ≈
α log10
(D/d)
(16)
From Eq. 5, α
is proportional to [(1/d) + (1/D)] / [log10 (D/d)] and the resonant impedance
is therefore
ZR ≈ (D/d) + 1
(17)
From inspection of Eq. 17, ZR approaches a minimum value as D/d approaches
unity.
The absolute value of the resonant impedance for a given set of conditions may
be computed from
ZR = R/2
(18)
where R is the total resistance of the line section.
From inspection of Eq. 2 it may be seen that R (and therefore ZR)
is minimum when d = D or D/d = 1.
The minimum antiresonant and the maximum resonant impedance of a coaxial transmission
line section is obtained when the conductor diameter ratio becomes infinitely large,
which corresponds to an infinitely large characteristic impedance. As may be seen
from Eq. 13 and 17, this occurs when D/d becomes infinitely large. This is shown,
with respect to a line having minimum attenuation, on Fig. 3 and Fig. 6.
Q Ratio
If in a tuned circuit the frequency is changed from the resonant frequency by
an amount Δf so that the power in the circuit is reduced to half
the value at resonance (or anti-resonance), then
Q = f / 2Δf
(19)
Defining Q of resonant (or antiresonant) transmission line sections in the same
way6,
Q = Z0/R * 2πl / λ
where 2πl / λ
is the angular length of the line section in radians and R is given by Eq. 2.
The Q is maximum when R/Z0 is minimum, but R/Z0 is proportional
to the attenuation of the line as shown in Fig. 3 and therefore the Q is maximum
when D/d = 3.592.
The Q of a coaxial transmission line section is minimum when the attenuation
of the line is maximum. As may be seen from Fig. 3, this occurs when D/d approaches
the limiting value, unity, and also when D/d becomes infinitely large.
References
(1) RMA Subcommittee on Antennas and R -F Lines-TR-31-2901 ; RMA Sub- committee
on Gas -Filled Transmission Lines-TR-911.
(2) E. J. Sterba and C. B. Feldman, Transmission Lines for Short Wave Radio Systems,
Proc. IRE, July 1932.
(3) C. R. Cox, Design Data for Beaded Coaxial Lines, ELECTRONICS, p 130, May
1946.
(4) F. W. Peek, Jr., "Dielectric Phenomena in High -Voltage Engineering," McGraw-Hill
Book Co., New York, Second Edition, p 28.
(5) P. H. Smith, U. S. Patent No. 2,298,428, issued Oct. 13, 1942.
(6) B. J. Witt, Concentric Tube Lines, Marconi Review, p 20, Jan. -Feb. 1936.
Fig. 5 - Solid-line curve gives effect of D/d on ratio of power-carrying capability
of line (based on voltage gradient of inner conductor) to that of line having maximum
capability. Dashed-line curve gives effect of D/d on ratio of Q of line to that
of line having minimum attenuation
Fig. 6 - Effect of D on ratio of anti-resonant impedance of line to that of line
having minimum attenuation
Posted August 9, 2023
|
















