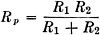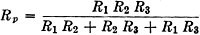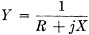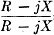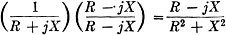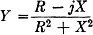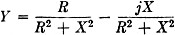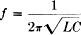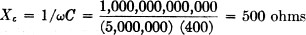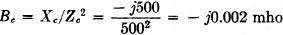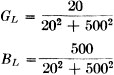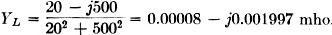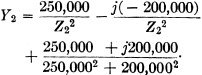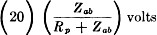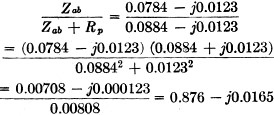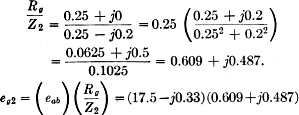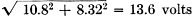June 1944 QST
 Table
of Contents Table
of Contents
Wax nostalgic about and learn from the history of early electronics. See articles
from
QST, published December 1915 - present (visit ARRL
for info). All copyrights hereby acknowledged.
|
When you read a lot of tutorials about introductory
electronics on the Internet, most are the same format where stoic, scholarly presentations
of the facts are given. Those of you who don't have enough fingers and toes to count
all of the college textbooks like that which you have read know of what I speak.
When hobby articles are written in a similar fashion, it can quickly discourage
the neophyte tinkerer or maybe even a future
Bob Pease. The
ARRL's QST magazine has printed a plethora of articles over the years that
are more of a story than just a presentation of the facts. My guess is the reason
is because often the authors are not university professors who have forgotten how
to speak to beginners. This article on basic calculations for AC series and parallel
circuits is a prime example.
A.C. Calculations for Parallel and Series-Parallel Circuits
Solving for Current at Voltage by Means of Admittance
By S.E. Spittle, * W4HSG
The problem of finding the resultant impedance of a group of impedances in parallel
is not usually discussed in the more elementary texts on alternating currents, probably
because the solution of such problems is rather lengthy and difficult without the
use of complex algebra. The term "complex algebra" may have a mysterious and rather
terrifying sound to those who have never heard of it, but actually the process is
comparatively simple for anyone having a knowledge of the elements of plain algebra.
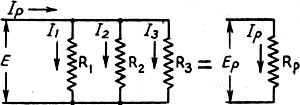
Fig. 1 - Parallel resistances.
The recent QST article entitled "Meet Mr. j"1 provides a good explanation
of the application of complex algebra to alternating-current circuits and should
be read as an introduction to this discussion. In that article one method of computing
the impedance of parallel circuits by means of their phase angles was described.
An alternative method, described here, makes use of the resistive and reactive components
without requiring a knowledge of the phase angles as such, and therefore can be
applied without the use of trigonometric tables.
Since the laws of alternating-current circuits are merely extensions of the laws
governing direct-current circuits, taking into account the effects produced by the
storage of energy in the electric and magnetic fields, it is logical to explain
the solution of a.c. problems in terms of the familiar operations used with d.c.
problems. For example, take a circuit consisting of two resistances, R1
and R2 in parallel, as shown in Fig. 1.
I1 = EG1
I3 = EG3
I2 = EG2
Ip = EGp
The usual formula for finding the parallel resistance of this combination is
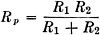
However, this formula is only a special case of the more general formula
1/Rp = 1/R1
+ 1/R2 + 1/R3 ... etc.,
applied to the case of only two resistances. In the special case of two resistances,
the second formula is converted into the first by means of a few simple transpositions;
When there are more than two resistances, the general formula is more practical,
as will readily be seen if we apply the same process to the case of three resistances.
Thus
1/Rp = 1/R1 + 1/R2
+ 1/R3
when transposed becomes
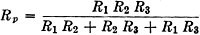
It may be interesting to note that the process of finding the resulting resistance
is the same as finding the total current in the parallel circuit, using any assumed
value of applied e.m.f. Thus
Ip = E/Rp =
E/R1 + E/R2 + E/R3.
Changing the value of E will change Ip but not Rp. Therefore
we can assume E to be one volt, giving the formula for the parallel resistance,
which is usually expressed as

The same formula can be applied to a number of parallel impedances in an a.c.
circuit, giving

The catch in this is that the currents in the various impedances are usually
not in phase with each other, so that the phase difference must be taken into account
in obtaining the correct value of parallel impedance. In the d.c. case the quantity
1/R is known as the conductance, represented by G whose unit of measurement is the
mho. Thus, a resistance of 5 ohms corresponds to a conductance of 1/5 or 0.2 mho.
The total conductance of a parallel circuit is the sum of the conductances of the
individual branches. Thus, making 1/R1 = G1, etc., we have
for three resistances in parallel
Gp = G1 + G2 + G3,
and the equivalent or parallel resistance, Rp, is equal to 1/Gp.
The conductance, G, is numerically equal to the current which would flow with one
volt applied to the circuit. Hence, in finding the total conductance of a parallel
circuit by adding the individual conductances we are merely following the same process
as in finding the total current by adding the individual currents. If this can be
done for d.c. circuits we should likewise be able to do the same thing for a.c.
circuits. In the latter case, 1/Z is called the admittance and is represented by
Y. Also, the total admittance of a parallel circuit is
Yp = Y1 + Y2 ... etc.
The value of Y is also measured in mhos, just as resistance, reactance and impedance
all are measured in ohms.
Here we remember our forgotten friend, the phase-angle. We know that if we apply
an alternating voltage to a circuit having several parallel branches, the absolute
values of the branch currents will add up to more than the absolute value of total
current unless all the currents happen to be in phase. Since the admittance is a
measure of the value of current that would flow in an impedance when one volt is
applied, it is necessary to add admittances in the same manner as we add currents
in a parallel circuit. The only practical ways of adding a number of currents, voltages
or impedances having various phase angles are by drawing scale diagrams or by splitting
each one into two components at right angles to each other, adding the two sets
of components separately and then combining the two sums by the familiar right-triangle
rule, or Pythagorean theorem. One component represents the condition of current
in phase with voltage, or 100 per cent energy consumption, and is often called the
real component . The other component represents the condition of current and voltage
90 degrees out of phase, or 100 per cent energy storage, and is often called the
imaginary component. This component is usually prefixed by the letter j to show
that it has been rotated 90 degrees with respect to the real component. The letter
j has been given the value of √(-1) and when it occurs in a computation it
is treated as a multiplier having this value, as has already been explained in the
article mentioned previously. Algebraic numbers having √(-1) as a factor are
known as imaginary numbers, which explains the name given the components of voltage,
etc., to which the letter j is applied. The method of adding the real and imaginary
components of voltage or current also is covered very well by Mr. Noll and therefore
only its application to parallel circuits will be discussed here.
In many problems of parallel impedance the mathematical solutions can be simplified
by the use of admittances. In this way frequent reference to trigonometric tables
is unnecessary, since phase angles no longer are factors in the computations. Practical
application of the method is discussed in this article and illustrated with typical
examples.
The preceding paragraph implies that we must split up each of our admittances
into two components before we can add them. To obtain the components of the admittance
we make use of the complex expression for impedance, which means the impedance when
split into its components of resistance and reactance. Expressed thusly,
Z = R + jX,
the j means that, if a diagram of the components of impedance is drawn, the reactance,
X, will be drawn at right angles to the resistance, R. Then,
since Y = 1/Z, the corresponding admittance would be
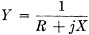
In order to get the complex expression out of the denominator we multiply the
fraction by
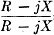
giving
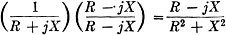
since j2 = -1. Now we have
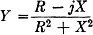
or
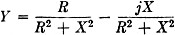
However, we know that
R2 + X2 = Z2.
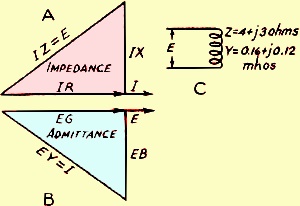
Fig. 2 - Impedance (A) and admittance (B) diagrams for the
coil (C). In the impedance diagram, the current, I, is used as the reference, while
the voltage, E, is used as reference in the diagram of (B).
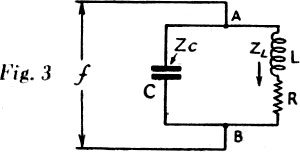
Fig. 3- RCL circuit.
Therefore the two parts of the admittance, Y, are R/Z2 and - jX/Z2.
If Z happened to be a pure resistance, X would equal zero, and R/Z2 would
become equal to R/R2 or 1/R, which is called G, or conductance in d.c.
circuits. The term R/Z2 is therefore called the a.c. conductance and
is also represented by the letter G. The term X/Z2, which is the reactive
or imaginary part of the admittance, is known as the susceptance and is represented
by B. Thus,
Y = G -jB,
where G = R/Z2 and B = X/Z2. Note that the phase angle
of the admittance is of sign opposite to that of the corresponding impedance.
2
Fig. 2 shows an impedance diagram at A and the corresponding admittance
diagram at B for a coil having 4 ohms resistance and 3 ohms reactance (C). The diagrams
are shown in terms of the components of voltage and current, and an applied e.m.f.
of 25 volts is assumed, so that both diagrams will be to the same scale.
To find the resultant impedance of a number of impedances in parallel, we add
the admittances of the individual branches to obtain the total admittance. The impedance
of the combination is then the reciprocal of the total admittance, or
Z = 1/Yt.
The application of this method will be shown by a couple of examples.
For the first example we shall take the tuned circuit of Fig. 3, consisting
of a condenser of 400-μμfd. capacity with negligible resistance, and a 100-microhenry
inductance coil having a resistance of 20 ohms. A circuit with these values will
be series resonant at 795.58 kilocycles, as can be verified by the formula for resonance,
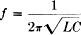
We shall now calculate the impedance of the circuit at this frequency, assuming
a voltage to be applied between the points A and B, making it a parallel-resonant
circuit. Since the factor ω = 2πf is used in calculating both inductive
and capacitive reactances, we start by computing its value as follows:
ω = (2) (3.1416) (795,580) = 5,000,000 (electrical
radians).
The impedance of the capacity branch is Rc - jXc
Rc = 0 and
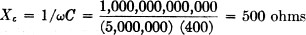
(There are 1,000,000,000,000 micromicrofarads in one farad). Therefore Z = 0
- j500 ohms. The admittance of this branch is
Yc = Gc - jBc
Gc = Rc/Zc2
= 0
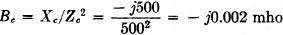
Therefore.
Yc = 0 - (- j0.002) = 0 + j0.002 mhos.
Since the impedance in this particular case is a pure reactance we could have
found B directly, since 1/Xc = ωC. This short cut cannot be used,
however, if the impedance also has a resistive component.
The impedance of the inductive branch is
ZL = RL +jXL
RL = 20 ohms and
XL = ωL = (5,000,000) (0.0001) henries
= 500 ohms.
so
ZL = 20 + j500 ohms.
The admittance
YL = GL -jBL
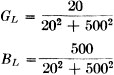
and
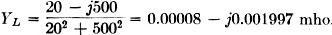
The admittance of the parallel circuit is
Yab = Yc + YL = (0
+ j0.002) + (0.00008 - j0.001997),
which is added thusly,
0 + 0.00008 + j0.0002 - j0.001997 = 0.00008 + j0.000003
mho.
The impedance then is

The result shows that the inductive and capaci-tive reactances in a parallel
circuit do not cancel out in the same manner as they do in a series circuit. This
results from the fact that the resistance in the inductive branch shifts the phase
of the current slightly, so that it is not exactly 180 degrees out of phase with
the current in the capacity branch. The current for a given applied voltage is equal
to E/Z or EY, since Y = 1/Z. Therefore a diagram of the relative values and phases
of currents in various parts of the circuit can be drawn by using the values of
Y to represent the currents, since current is proportional to Y.
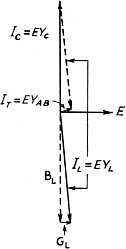
Fig. 4 - Vector diagram of the currents in the various branches
of the circuit of Fig. 3.
Fig. 4 is such a diagram, with the conductance and total current exaggerated
to show the effect of resistance in the circuit. Actually the frequency at which
the resultant reactance is zero is so close to the frequency at which XL
= Xc that for all practical purposes they can be considered identical
except in circuits having lower values of Q than are ordinarily used in radio work.
Such low-Q circuits are, however, found in television amplifiers and are also likely
to be found in audio-frequency work.
A second example, illustrating a series-parallel circuit, is the resistance-coupled
amplifier shown in Fig. 5. An exact calculation for such an amplifier, taking
into account all possible current paths, is quite complicated, so that it is customary
to reduce the amplifier to a simplified circuit which approximately represents the
conditions existing for the frequency of interest. For low frequencies the circuit
of Fig. 5 can be represented by Fig. 6, where the applied voltage is the
a.c. voltage developed between plate and cathode by a signal, and is equal to μ
times the a.c. voltage applied between grid and cathode.
The voltage eg2 between grid and cathode of the following tube is
practically equal to the voltage drop across the grid leak, since the voltage across
the cathode bypass condenser is negligible if the bypass condenser has a fairly
large capacity (considering the drop caused by the applied grid voltage only). This
voltage will, therefore, be a portion of the voltage between A and B and will then
depend upon the frequency as well as the constants of the circuit. Assuming the
frequency of the applied signal to be 53 cycles per second, the reactance of the
coupling condenser will be 200,000 ohms. With an applied signal of 1 volt and an
amplification factor of 20 the amplified a.c. voltage applied to the network of
Fig. 6 will be 20 volts. This voltage will be divided between the internal
resistance of the tube, Rp, and the impedance, Zab, between
points A and B.
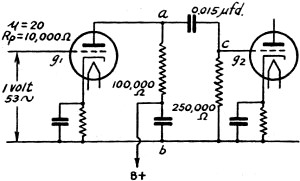
Fig. 5 - Resistance-coupled amplifier circuit.
The admittance Yab, will be the sum of the admittances of the two
branches, one being the plate-coupling resistance, R1, and the other
consisting of the grid leak, R2, in series with the coupling condenser.
For the first branch
Z1 = R1 = 100,000 + j0 ohms and
Y1 = 0.00001 - j0 mho.
For the second branch
Z2 = R2 - jX2 = 250,000
- j200,000 ohms and
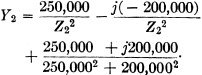
The calculations for a high impedance such as this can be performed more conveniently
by expressing the impedance in megohms. The corresponding admittance will then be
in micromhos. Thus,

and Y1 = 10 - j0 micromhos.
Then
Yab = Y1 +
Y2 = 10 + j0 + 2.44 + j1.95 + 12.44 + j1.95 micromhos.
The impedance between points A and B will be

In order to find the voltage eg2 we must first find the voltage between
the points A and B. The impedance Zab in series with the plate resistance
Rp forms a voltage divider. Therefore, the voltage across Zab
will be equal to
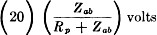
Rp is 10,000 ohms resistance or 0.01 + j0
megohms. Therefore,
Zab + Rp = 0.0884 - j0.0123 megohms.
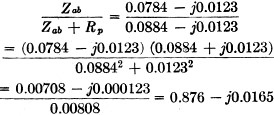
eab=(20) (0.876- j0.0165) =17.52- j0.33
volts.
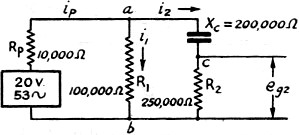
Fig. 6 - Equivalent circuit of the resistance-coupled amplifier
in Fig. 5 for low frequencies.
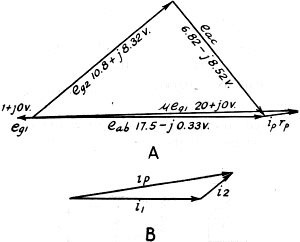
Fig. 7 - Vector diagrams useful in checking calculations.
(A) shows the relative values of voltage in the circuit of Fig. 6, while (B)
shows relative currents.
The voltage eab is the sum of eg2 and the voltage drop
across the coupling condenser since they are in series. Therefore,
eg2 = (eab) (Rg/Z2)
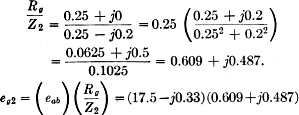
The absolute value of this voltage is
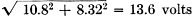
The overall amplification or ratio of voltage at grid No. 2 to that at grid No.
1 will then be 13.6, since one volt was assumed to be applied to grid No. 1. The
voltage at grid No.2 will lead the voltage at plate No.1 by an angle whose tangent
is

It is not necessary to find any phase angles to determine the voltage or current
anywhere in the circuit. In fact, the relative phase of any voltage in the circuit
can be found by graphical methods with sufficient accuracy for ordinary purposes.
The fact that the voltages are expressed as complex quantities makes it easy to
draw a scale diagram of the various voltages in the circuit. Such a diagram is useful
for checking the accuracy of the calculations. A diagram of the voltages in this
circuit is shown in Fig. 7, and a diagram of the relative currents is shown
in Fig. 8. The values of alternating current in microamperes can be found
by multiplying the admittance in micromhos by the applied e.m.f. of 20 volts (I
= EY). The voltages and currents considered in this problem are, of course, only
the alternating parts of the pulsating voltages and currents in the actual amplifier.
The d.c. values have no other effect than to establish the values of Rp
and μ and to determine the amplitude of voltage that can be applied before distortion
begins.
In practical work the performance of amplifiers is ordinarily computed by means
of graphs or approximate formulas rather than such detailed calculations. The examples
given above were used instead of the usual problems concerning miscellaneous collections
of inductance and capacity because they are typical of the circuits actually found
in radio equipment, and thus should indicate that the methods of calculations illustrated
have practical applications.
One desirable feature of using complex notation is that it eliminates the necessity
for extracting square roots except for one such operation as the last step in the
calculations, when the absolute value of current or voltage is desired, as is usually
the case. A vector diagram of all the values in the problem should be drawn as a
check on the calculations and to make sure that plus signs have not been slipped
in where there should be minus signs or vice versa. Such errors are usually readily
apparent as soon as construction of the diagram is attempted. The vector diagram
need only be drawn roughly to scale, and may be in terms of voltages, currents,
impedances or admittances, whichever is most convenient.
* ·12 Griggs St.. Allston 34, Mass.
1 Noll, "Meet Mister j," QST, October, 1943, p. 21.
22 B is sometimes defined as - X / Z2, making Y = G + jB, This
of course, is equivalent to the relation given above.
Posted September 28, 2019
(updated from original
post on 10/5/2012)
|