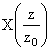RF Cascade Workbook for Excel
RF & Electronics Symbols for Visio
RF & Electronics Symbols for Office
RF & Electronics Stencils for Visio
RF Workbench
T-Shirts, Mugs, Cups, Ball Caps, Mouse Pads
Espresso Engineering Workbook™
Smith Chart™ for Excel
|
 |
Z-Transform Properties |
In mathematics and signal
processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex
numbers, into a complex frequency-domain representation. It is like a discrete equivalent of the Laplace
transform. This similarity is explored in the theory of time scale calculus. The Z-transform was introduced, under
this name, by Ragazzini and Zadeh in 1952. The modified or advanced Z-transform was later developed by E. I. Jury,
and presented in his book Sampled-Data Control Systems (John Wiley & Sons 1958). The idea contained within the
Z-transform was previously known as the "generating function method".
- Wikipedia
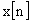 |
↔ |
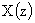 |
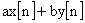 |
↔ |
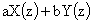 |
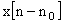 |
↔ |
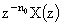 |
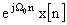 |
↔ |
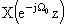 |
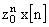 |
↔ |
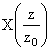 |
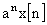 |
↔ |
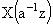 |
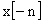 |
↔ |
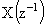 |
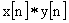 |
(convolution) |
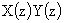 |
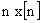 |
↔ |
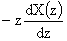 |
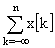 |
↔ |
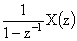 |
|

|

Copyright: 1996 - 2024
Webmaster:
Kirt
Blattenberger,
BSEE - KB3UON
RF Cafe began life in 1996 as "RF Tools" in an AOL screen name web space totaling
2 MB. Its primary purpose was to provide me with ready access to commonly needed
formulas and reference material while performing my work as an RF system and circuit
design engineer. The World Wide Web (Internet) was largely an unknown entity at
the time and bandwidth was a scarce commodity. Dial-up modems blazed along at 14.4 kbps
while tying up your telephone line, and a nice lady's voice announced "You've Got
Mail" when a new message arrived...
|
All trademarks, copyrights, patents, and other rights of ownership to images
and text used on the RF Cafe website are hereby acknowledged.
|
|
All trademarks, copyrights, patents, and other rights of ownership to images
and text used on the RF Cafe website are hereby acknowledged.
My Hobby Website: AirplanesAndRockets.com
My Daughter's Website: EquineKingdom
|
|
|


 |