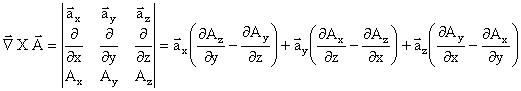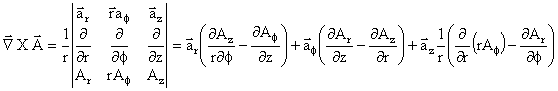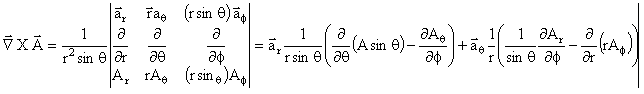|
In vector calculus, the curl (or rotor) is a vector operator that describes the rotation of a vector field. At every
point in the field, the curl is represented by a vector. The attributes of this vector (length and direction) characterize
the rotation at that point.
The direction of the curl is the axis of rotation, as determined by the right-hand rule, and the magnitude of
the curl is the magnitude of rotation. If the vector field represents the flow velocity of a moving fluid, then
the curl is the circulation density of the fluid. A vector field whose curl is zero is called irrational. The curl
is a form of differentiation for vector fields. The corresponding form of the fundamental theorem of calculus is
Stokes' theorem, which relates the surface integral of the curl of a vector field to the line integral of the vector
field around the boundary curve. - Wikipedia
"Ñ" is a vector and is pronounced "del." The vector function is A(x,y,z),
A(r,Φ,z), or A(r,θ,Φ)
|