|
In several fields of
mathematics the term permutation is used with different but closely related meanings. They all relate to the
notion of mapping the elements of a set to other elements of the same set, i.e., exchanging (or "permuting")
elements of a set. In combinatorial mathematics, a combination is an un-ordered collection of distinct
elements, usually of a prescribed size and taken from a given set. (An ordered collection of distinct elements
would sometimes be called a permutation, but that term is ambiguous.) Given such a set S, a combination of
elements of S is just a subset of S, where, as always for (sub)sets the order of the elements is not taken into
account (two lists with the same elements in different orders are considered to be the same combination). Also, as
always for (sub)sets, no elements can be repeated more than once in a combination; this is often referred to as a
"collection without repetition". For instance, {1,1,2} is not a combination of three digits; as a set this is the
same as {1,2,1} or as {2,1,1}. On the contrary, a poker hand can be described as a combination of 5 cards from a
52-card deck: the order of the cards doesn't matter, and there can be no identical cards among the 5.
- Wikipedia
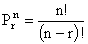 |
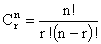 |
| Where: n = total number of items in the group R =
number of items chosen from the group
|
|









