Theory and Application of U.H.F., June 1945 Radio News

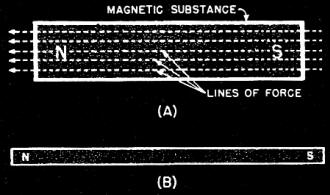
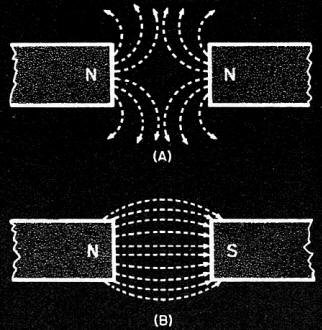
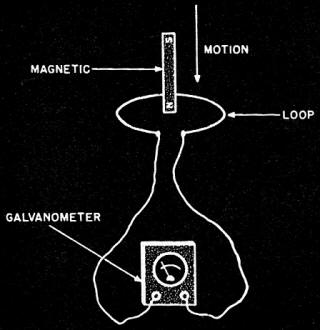
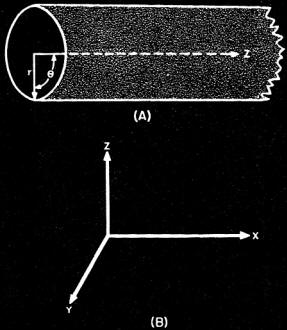
This is the final installment of an 11-part series in Radio News magazine entitled "Theory and Application of U.H.F.," written by Milton Kiver. It spanned from December 1943 to June 1945. Topics included basic electrical, magnetic, and electromagnetic theory, cavity resonators as tuning units of klystron and magnetron oscillators, waveguide, free space propagation, high frequency amplifiers, transmission lines, and coupling energy to/from cavity resonators. As the list suggests, there was a great concentration on field theory. Being that the Radio News readership covered a broad range of experience and education, Mr. Kiver went light on use of equations and heavy on use of diagrams, charts, and textual descriptions. Everything described throughout the series is as valid and applicable today as it was 75 years ago, so it is still worth reading.

Eleven installments appeared in the following issues: Part 1: December 1943 (p35), 2: January 1944 (p32), 3: March 1944 (p41), 4: April 1944 (p46), 5: May 1944 (p50), 6: August 1944 (p53), 7: October 1944 (p58), 8: December 1944 (56), 8: February 1945 (p58), 10: April 1945 (p57), 11: June 1945 (p57). I hope to eventually procure those editions and post the articles.

Theory and Application of U.H.F. - Part 11. The concluding article of this series, describing the operation of electromagnetic-wave travel through wave guides or space.

Fig 1 - (A) The direction of magnetic lines of force through a magnet. (B) Showing how a long, thin magnet is generally used to approximate separate north and south poles.

Fig. 2 - Showing the repulsion and attraction between magnetic poles.

Fig. 3 - Magnetic lines of force are continuous and form closed paths.

Fig. 4 - A simple arrangement which indicates the relationship between changing magnetic fields and induced e.m.f.'s.

Fig. 5 - Two commonly used systems of coordinates: (A) rectangular: (B) cylindrical.

All the magnetic fields discussed so far were brought about by moving electric charges. Let us investigate the magnetic fields that are brought about by magnetic charges or magnetic substances.

To correspond to the field of electrostatics there is magneto statics, which deals with magnetic charges and magnetic fields at rest. As far as is known today, there are no separate north and south poles corresponding to negative and positive charges. Wherever a magnetic north pole is found there is likewise found a south pole attached to it in some form or manner. Thus, if a magnet is taken and split in two it is found to have, at one end, north magnetism and at the other end south magnetism. However, it is possible to take a very long narrow magnet with the north and south poles relatively far from each other and in this way approximately separate north and south poles. (See Fig. 1.)

Analogous to the electric charge, it is also found that the north and south poles of magnets give rise to fields of force, called magnetic fields. By means of these fields, north poles will repel north poles and attract south poles. (See Fig. 2.) It is also found that these lines of force, also called magnetic lines of flux, start out from the north pole and go in through the south pole and then back to the north pole and so on around.

A difference is noted here between lines of electric force and those connected with magnets. If there was one electric charge in space then the lines of force would all radiate away from the charge and would continue indefinitely. In the magnetic case, the lines of flux must form complete rings since connected with every north pole there is attached to it, in some manner, a south pole. Any lines emanating from the north pole go back to the south pole and through the material to the north from which they started. Thus, they have no end and in this sense are said to be continuous. This is shown in Fig. 3.

Analogous to the electrostatic case, the fields and forces set up by these poles or magnets affect only other magnetic substances and nothing else. If a magnet were taken and placed in a field that contained stationary electrons it would be found that each had no effect on the other. As long as these two fields are at rest, relative to each other, there is no interaction. It is only when they move that these forces are found to clash.

It has just been pointed out that an electric current gives rise to a magnetic field and so it occurred to Faraday in 1831 that a magnet might, under some conditions, give rise to an electric current. While the magnet was at rest there were no effects noticed, but when this magnet moved relative to some piece of wire, a current was noted on a galvanometer, which is a current-measuring device. Moving the magnet in one direction produced a current which reversed when the magnetic field was reversed. Currents produced this way are called induced currents and the e.m.f.'s that caused these currents to flow are called induced e.m.f.'s. The formula by which Faraday stated these effects is known as Faraday's law and in words states that the electromotive force induced by changing the flux density through a fixed circuit is equal to the time rate of change of this flux.

Faraday's results can be obtained by using the simple setup of Fig. 4. When the magnet is moved relative to the coil, there will be an e.m.f. induced in the coil of wire by the changing magnetic field or flux. If the wire is a good conductor, a certain amount of current will flow. Making the wire from a poor conductor will still give rise to the same e.m.f. but now a smaller current will flow since there is more resistance in the circuit and we know from Ohm's law that if the e.m.f. is constant, the current is then inversely proportional to the resistance.

Continuing in this direction, it can be seen that if finally a perfect non-conductor is used where the conducting wire was held formerly, there would still be found an e.m.f. induced even if no current flow resulted from it. The e.m.f. set up is the electric field and so it can be seen that a varying magnetic field will give rise to an electric field in a direction normal to itself. The electric field is constant if the rate of change of the magnetic field is constant and will vary in intensity if the rate of change of the magnetic field varies. The frequency of both fields is the same.

It is important to remember when mentioning the time rate of change of a magnetic field that several means may be used to bring about this change. First, of course, the magnet producing this flux can be caused to move and this was the illustration mentioned above. Next, the same results can be obtained by keeping the flux constant and fixed and moving the coil of wire across this field. In this case, the induced e.m.f. will be proportional to the number of flux lines cut per unit time, say a second (this is related directly to the speed the coil is traveling), and the angle at which the flux lines are cut. If the coil is moved parallel to the lines, then no e.m.f. will be induced. If the coil moves at some angle to the field then the induced e.m.f. will be proportional to the angle, the best results being obtained when this angle is 90°.

The above ideas should serve to clarify the meaning of the phrase, time rate of change of the magnetic field.

The above discussion has given all the formulas necessary to state the complete set of equations that form the basis of all electromagnetic theory and which are so often referred to as Maxwell's equations. Although it has not been stated before, Maxwell took the laws stated above and generalized them so that they would be applicable to any set of coordinates. Most people are familiar with the simple rectangular coordinate system such as is obtained by having x and y axes at right angles to each other. For three dimensions a z axis is added which is at right angles to the above x and y axes.

However, when dealing with cylindrical pipes, it is easier to work with cylindrical coordinates whereby points in the system are expressed in terms of the radius of the cylinder and the angle that we must turn from the starting point. There may be other systems that could be used but there is no necessity for discussing these at this point. Fig. 5 illustrates the rectangular system and cylindrical system. Maxwell took Gauss' law, Faraday's law and Ampere's law and generalized them to fit these various three-dimensional systems.

1. For free space where there are assumed to be no free charges, the number of electric lines of fiux entering any region is equal to the number of lines leaving.

44. A magnetic field that is changing in value will develop an electric field that is normal to both the direction of motion of the magnetic field and the field itself.

The great significance of these equations lies in the fact that from them the properties of electromagnetic wave travel through space can be accurately predicted. With one clean sweep, they eliminate the need for electric currents to be actually in the immediate vicinity in order to explain the presence of magnetic fields that may be encountered. Electric fields that are changing in magnitude (with time) will readily accomplish the same result.

In ultra-high-frequency work, extensive use is made of wave guides in transmitting energy from one place to another. So long as the boundary conditions of these wave guides are taken into account when setting up Maxwell's equations, the correct results can be derived in advance. This not only serves to bring out the underlying equality of all radio waves, no matter how they are generated or transmitted, but it also provides us with a convenient means of determining in advance, whether one shape of wave guide will prove more suitable than another. This is very important in many of the present applications of high-frequency waves and will prove of inestimable value in the postwar era, when greater application of u.h.f. devices will be widely used.

It should be kept in mind that the set of equations put forth by Maxwell are, in a sense, generalizations of or-dinary, everyday electric theory. Problems involving transmission lines can just as readily be solved using electric and magnetic fields as with the corresponding electric currents. The only reason this is seldom done is due to the greater complexity involved when fields are used than for electric currents. It might be added, too, that the general unfamiliarity with Maxwell's equations, even today, has tended to becloud them with an unnecessary air of mystery.

Some idea as to the way the waves travel may now be had from Maxwell's equations 3 and 4. If the changing electric field gives rise to a magnetic field and the magnetic field so produced gives rise to an electric field, all occurring in the same region, then it may be wondered just how the wave will be propagated through space. But, if, instead of the varying electric field producing the magnetic field just in the same region, suppose it also produced a magnetic field a little removed from it and the magnetic field so generated gave rise to another electric field, also a little farther on, then it is possible to see something of the way the propagation takes place. Each varying field gives rise to the other varying field a little farther on and so each sustains the other and the wave moves along with the velocity of light in free space. If conditions are such as to prevent the formation of one field, then the other will likewise be prevented from existing since the energy from one moves to the other. On the average, each field sustains half the total energy.

Another idea before Maxwell was the idea of speed. It is known that the moving charges give rise to a magnetic field through their electric field, and that this magnetic field can be felt at some distance from the wire. The question that he wished to answer was whether this magnetic field was produced at some distance from the source as soon as the charges started to move, or whether there was some time lapse. Actual measurements gave no results since the apparatus involved could not cope with the extremely small time interval between the start of the charge and the appearance of the magnetic field. Maxwell showed on paper that by the use of his electromagnetic equations, the speed of these waves should be equal to the speed of light in free space and this is in the vicinity of 186,000 miles per second. Maxwell never proved this by actual measurement, but Hertz did 25 years later and his experiments led to the acceptance of Maxwell's theory. By means of further experiments it was immediately shown that all optical laws were obeyed by these electromagnetic waves and this, of course, led to the final conclusion that light was also an electromagnetic wave.

It might also be stated here that the ratio of the electromagnetic unit of current to the electrostatic unit of current is also equal to the velocity of light, and this was another fact that got Maxwell started on the trail of his set of equations. The medium that Maxwell envisioned the waves to travel in - free space - was called the ether. His idea of the makeup of this nebulous substance, however, is not quite what we think of it today, but since the laws still hold, it is best to forget, or at least avoid, saying any-thing about the space or medium or ether that the waves travel in and just stick to the waves themselves. This is a question that still has not been answered to everyone's satisfaction.

This, then, is the electromagnetic theory as set forth by Maxwell, and which is receiving so much attention at the ultra-high frequencies. The laws were based on simple electrical phenomena and do not represent the work of one man alone. It is doubtful that anyone person could evolve all this theory. It required the work of many men, a fact that is true of all fields of endeavor. It is hoped that by a better understanding of what underlies all this theory it will be possible to more easily visualize what goes on in our high-frequency apparatus.

This series, which is now being concluded, has attempted to present the basic ideas of the operation of ultra-high-frequency radio apparatus in nonmathematical language. The simple radio circuits used in ordinary, everyday equipment are still present in ultra-high-frequency apparatus, but in a modified form that make these components suitable for the shorter wavelengths.

Of necessity, due to present war conditions, many advancements and refinements which have already been made in the various tubes described in these articles cannot be told now. Later, when conditions become normal again, restrictions will probably be lifted and the complete story will be available. For the present, best advantage may be taken of those articles and books that do appear, so that when this later information is released, it will fall into a familiar pattern. This is especially urged for those persons who intend to enter the ultra-high-frequency field after the war. A list of the available books is given at the end of this article with an added note as to the complexity of each one.

There have been two proposals advanced recently that pertain directly to the ultra-high frequencies. One is a proposal to allot ether space around 10,000 mc. to servicemen and women to be used by them without the necessity of applying for licenses, as is the custom at the lower amateur bands. The present amateur bands were quite congested before the war and they promise to become even more so after the war, what with the thousands of newcomers to the field of radio and radar. Sufficient ether space could be easily found at 10,000 mc.

The second proposal relates to the use of the higher frequencies by the television interests. The Television Panel of the Radio Technical Planning Board (RTPB) has advanced the following proposed allocations to be used for television relay service.

2, A second group of twenty 10-mc. continuous channels to be located somewhere between 300 and 1000 mc.

3. A group of twenty 20-mc. continuous channels to be located between 1000 and 3000 mc.

In addition to the above, experimental stations are to be given space at other frequencies where they will be permitted to experiment with ideas in attempts to improve the present television methods.

With television and the present radio detection devices vying for use of the ultra-high frequencies, there promises to be plenty of work and jobs for all radiomen who have some knowledge of the operation of radio apparatus at these extremely short wavelengths. The old adage about a word to the wise is sufficient is even more applicable here. In closing, the editors of Radio News wish to add that future articles on u.h.f. radio will be presented as soon as the material becomes available.

This book merely assumes a simple knowledge of radio and then goes on from there to give word descriptions of the operation of ultra-high-frequency radio.

This book describes the operations of electric waves, showing the foundations of Maxwell's equations. While only a moderate use is made of mathematics, the examples found require a knowledge of calculus. U.h.f. radio apparatus is not described directly, but the travel of electric waves in wave guides. is brought out.

Hyper and Ultra-High Frequency Engineering - Sarbacher and Edser. John Wiley & Sons.

The last four volumes are excellent works on the subject but they all require extensive mathematical backgrounds and would be quite out of reach of the ordinary radioman.

Theory and Application of U.H.F.June 1945 Radio News

Theory and Application of U.H.F.
June 1945 Radio News